2009-03-20 19:03| 
15 Comments | 本文内容遵从摘录几道题目。
计算1·2^2 + 2·3^2 + 3·4^2 + ... + 19·20^2
原式 = (1^3 + 2^3 + ... + 20^3) - (1^2 + 2^2 + ... + 20^2) = 44100 - 2870 = 41230
求2^x = 3^y - 1的所有正整数解
x=1时(1,1)是一个解；当x>1时，方程模4后左边永远等于0，右边则是(-1)^y - 1，可知y为偶数。令y=2z，那么有2^x = (3^z - 1)(3^z + 1)，这就要求3^z-1和3^z+1都是2的幂；但它们只相差2，因此它们只有可能是2和4，于是z=1，即原方程的另一个解为(3,2)。
圆周上有2008个点。选择两个点连成一条线，再选另外两点连一条线，这两条线段相交的概率为多少？
给定四个点，在三种连接方案中恰有一种会发生相交。取遍所有C(2008,4)种组合，相交的总情况数总是占了1/3，因此所求的概率就是1/3。
我们称一个正整数为“吉祥数”，如果它的二进制表达中有偶数个“1”。第2009个吉祥数是多少？
注意到两个正整数2k和2k+1的二进制表达中就只有最后一位不同（一个是“0”一个是“1”）。因此，2和3里面恰有一个吉祥数，4和5里面恰有一个吉祥数……以此类推，第2009个吉祥数必然是4018和4019中的一个。验证可知，4018=(111110110010)2，它有偶数个“1”，因此4018即为答案。
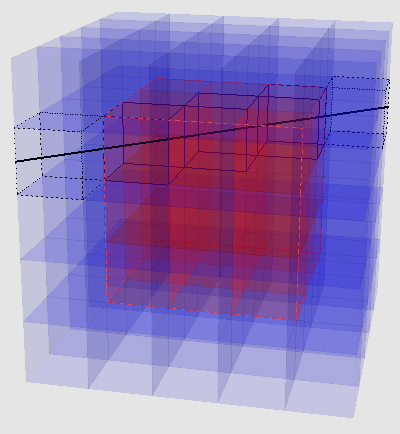
在R^n的井字棋游戏中有多少种取胜的方式？换句话说，在3*3*...*3的n维立方体棋盘中，选取三个排成一条线的小立方体有多少种可能？
给出一个我自己的解法：想象给这个立方体套一个边长为5的“外壳”，则原棋盘的每一条直线延长后都对应了外壳上的两个小立方体，外壳上的每一对位置相对的小立方体反过来也都对应着里面的棋盘中的一条直线。因此，答案为外壳上的立方体个数除以2，即(5^n-3^n)/2。
汗……图片隐藏不了……
来源：http://web.mit.edu/hmmt/www/datafiles/solutions/2009/solutions-guts-2009.pdf,
沙发
另外最后一题是以前做过的奥赛题的说- -! 但是这个思路确实很美妙 = =！
圆周上选两个点连了一条线，就把整个圆分成了两半，如果另外两个点分属于这两半的点集则肯定相交，否则不相交。
这答案藏得真邪恶。。。
占个位
图片可以放个链接上来猛击才看大图啊
或者是缩略图
思路都很妙的说.不过不是特难.还是要说那本匈牙利数学奥林匹克题集啊..这几天晚自习做那个都快疯掉了.默哀我单调递减的数学思维.
图怎么做的……很漂亮啊
题好神奇的说
6楼的，我觉得还是CMO比较变态的说
第一题MS解法有误……
原式 = (2^3 + ... + 20^3) - (2^2 + ... + 20^2)
第一题不是东南赛区的一题么。差分就好
话说 怎么看答案的啊
下次发选中才看得见的行不？缩略图太难看……单击显示也行啊……
最后一题思路不对
我看错了，最后一题思路没错。