环面多面体,即亏格为 1 的多面体,直观地说就是有 1 个洞的多面体。下图中三个多面体里分别有 0 个洞、1 个洞和 2 个洞。第二个多面体就是环面多面体。最近,我在研究一些和环面多面体相关的话题,在这里和大家分享一些我的发现。
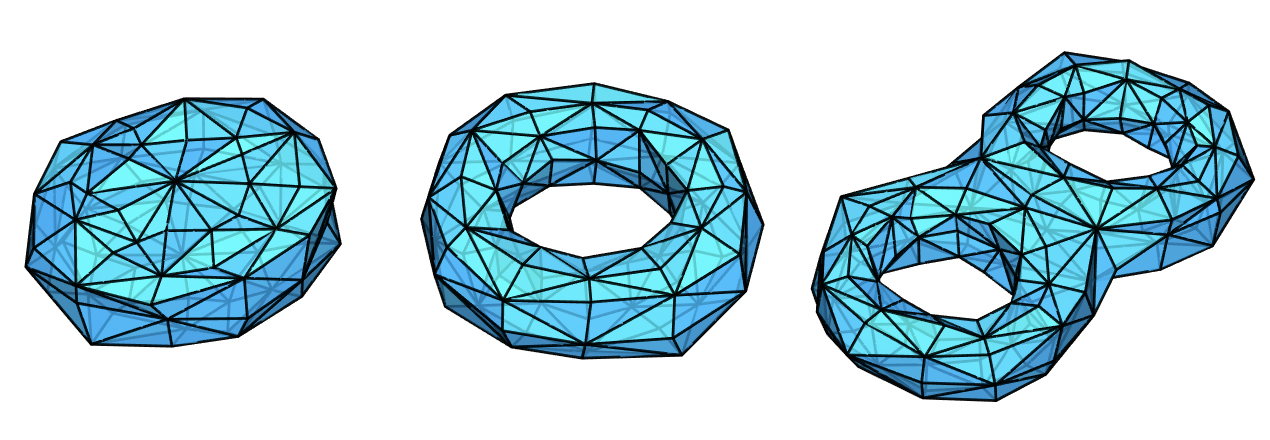
由正多边形构成的环面多面体
正四面体、正六面体、正八面体、正十二面体、正二十面体、侧面均为正方形的正棱柱、侧面均为等边三角形的正棱锥、足球或者 C60 所对应的多面体等等,都是由正多边形构成的多面体。
有没有什么环面多面体也是由正多边形构成的呢?一个容易想到的做法就是,把 8 个正方体摆成一个“口”字形。这样做是不行的。正方体拼接起来后,原来的很多面会因为共面的原因合成了更大的面。站在整个多面体的角度来讲,它的各个面就不再是正多边形了。
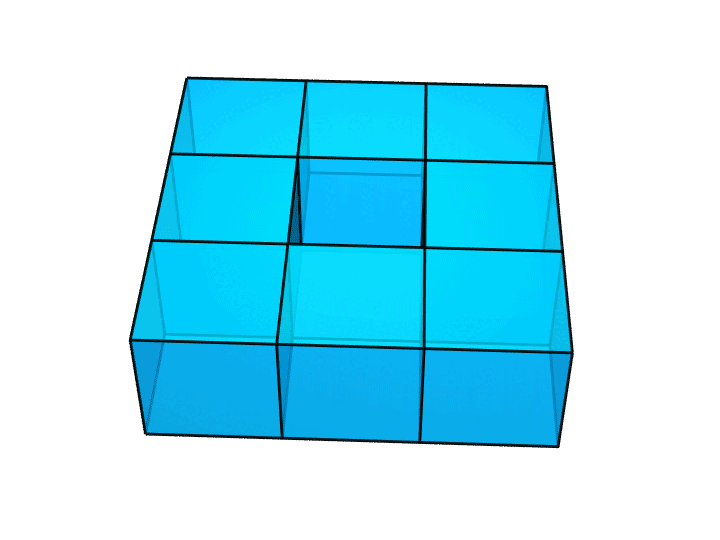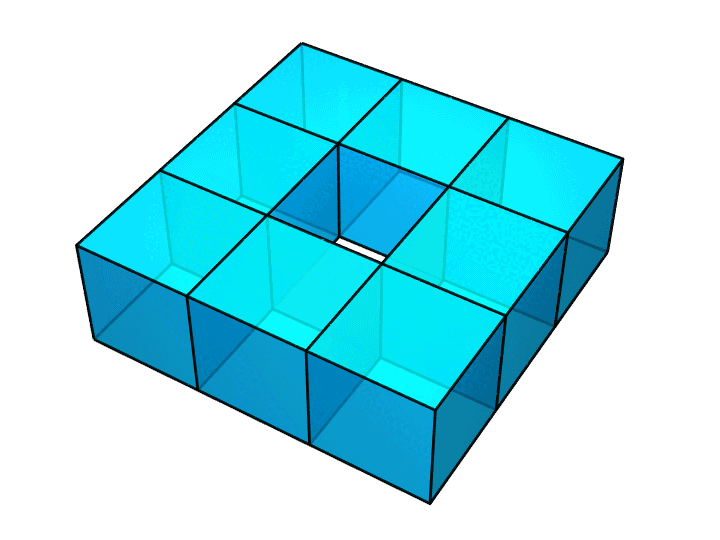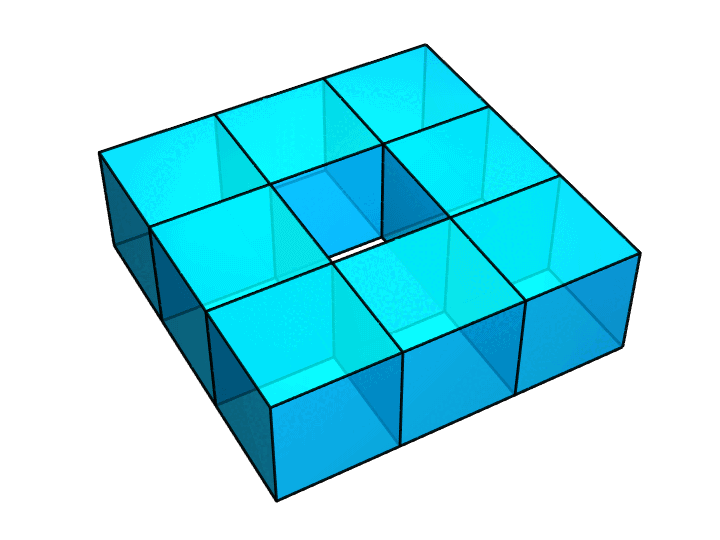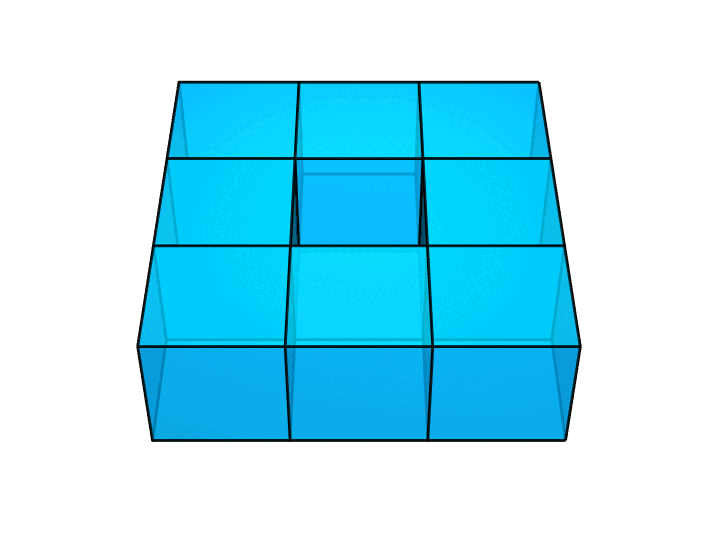
然而,如果我们用下面这样的方法把正方体拼接起来,就漂亮地绕开了这个问题。
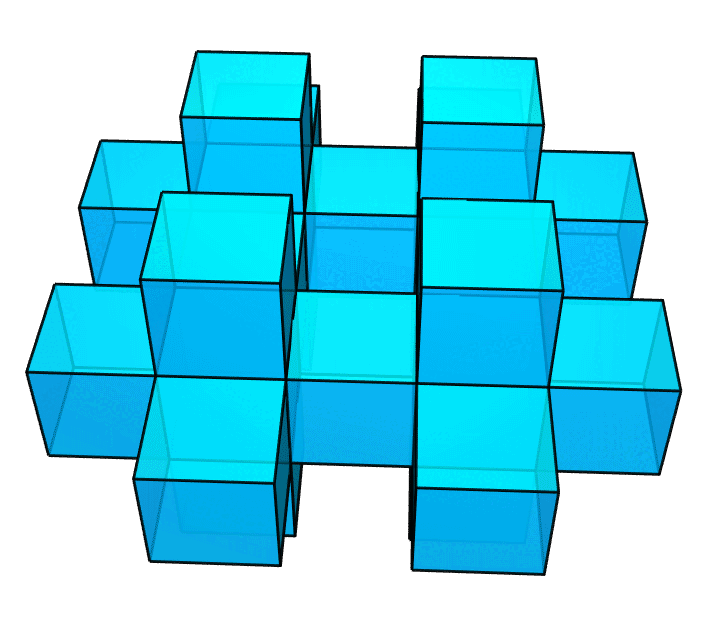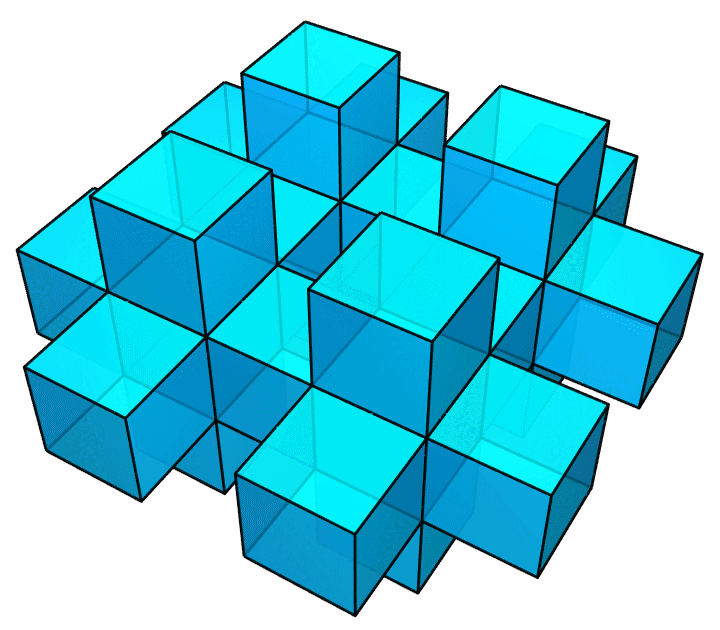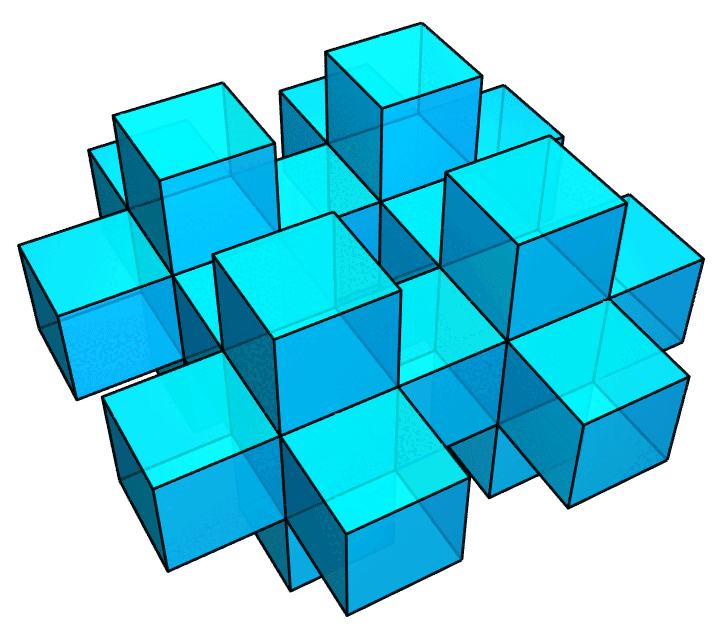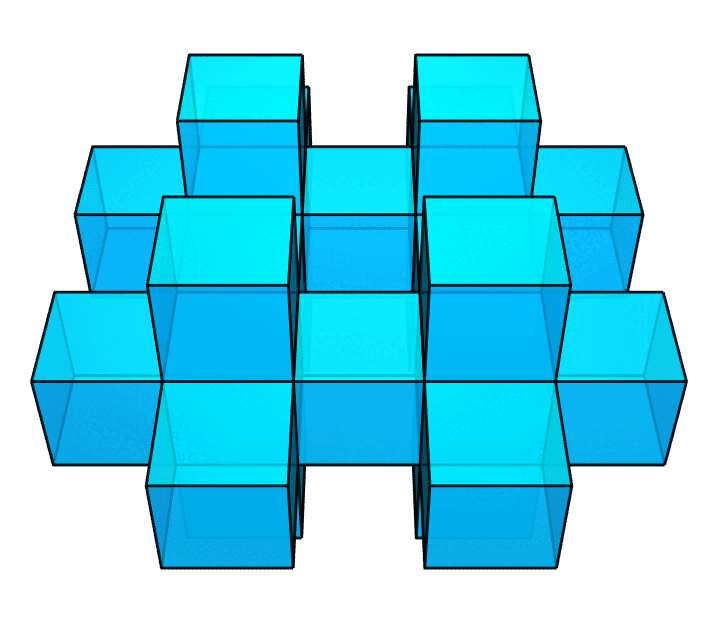
做完上面这个图之后,我才发现这个图是有毛病的。作为一个完美主义者,我又重新做了一个正确的图,如下图所示。你能看出这两个图的区别吗?
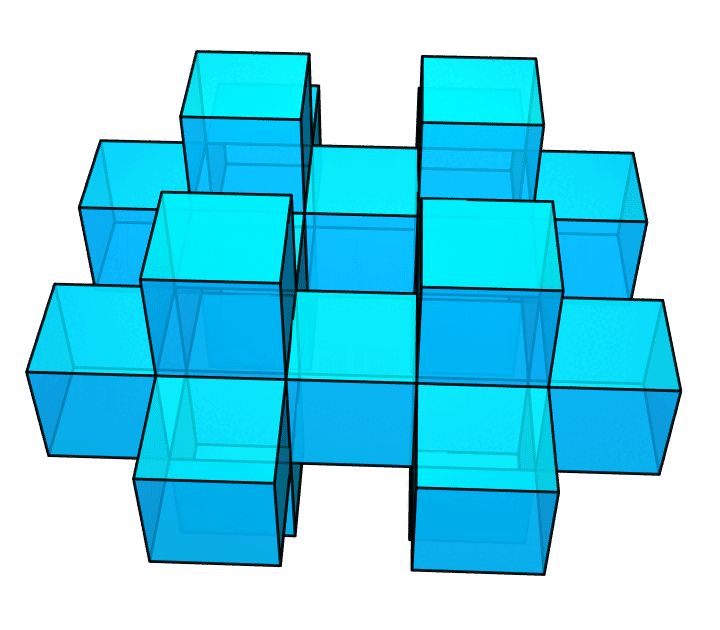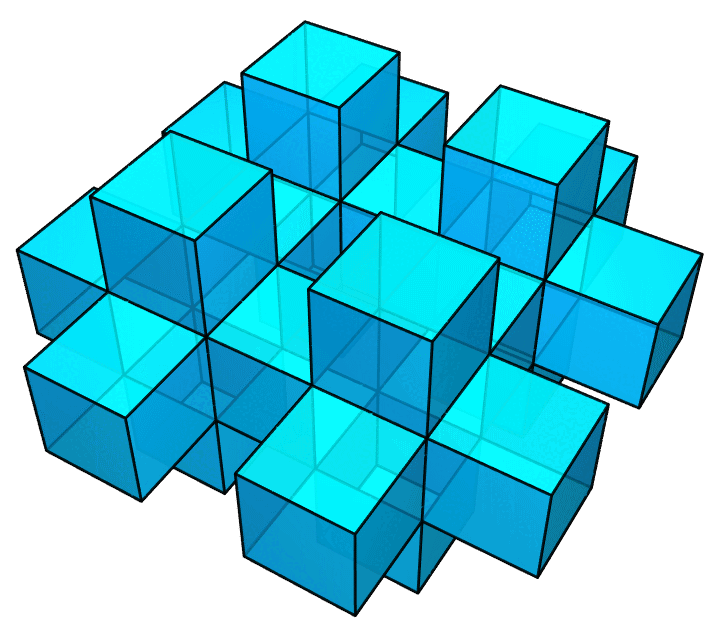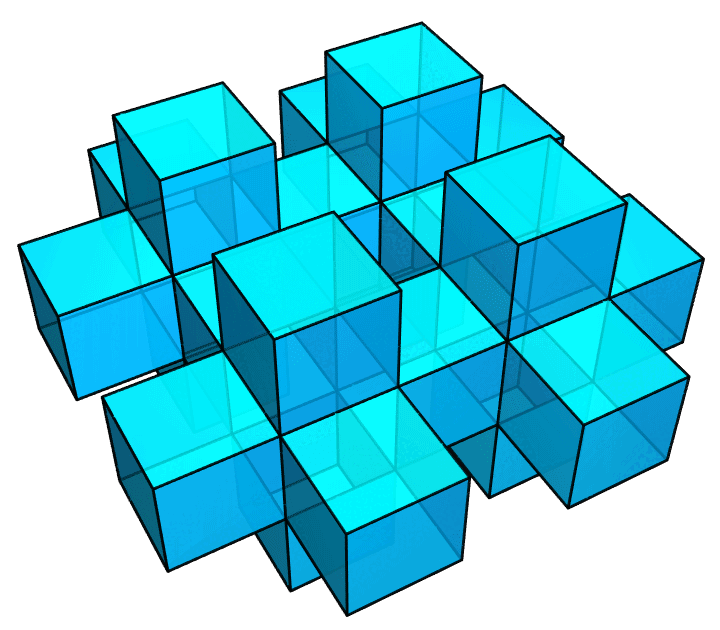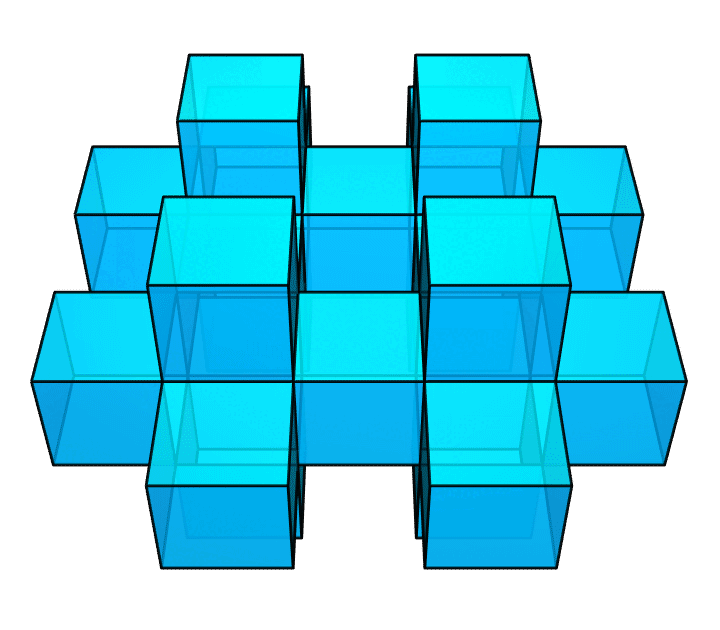
答案是,前一个图里,相邻小正方体的公共面,即那些贴合在一起的面,仍然留在了图中;作为一个真正的多面体,它的内部是不该有这些面的。所以,我才做了后面这个图。它里面就是空的了。
利用拼接的方法,还能做出更多满足要求的环面多面体。例如,将 6 个正六棱柱(侧面均为正方形)按照下图的方式拼成一圈,也形成了一个满足要求的图形。
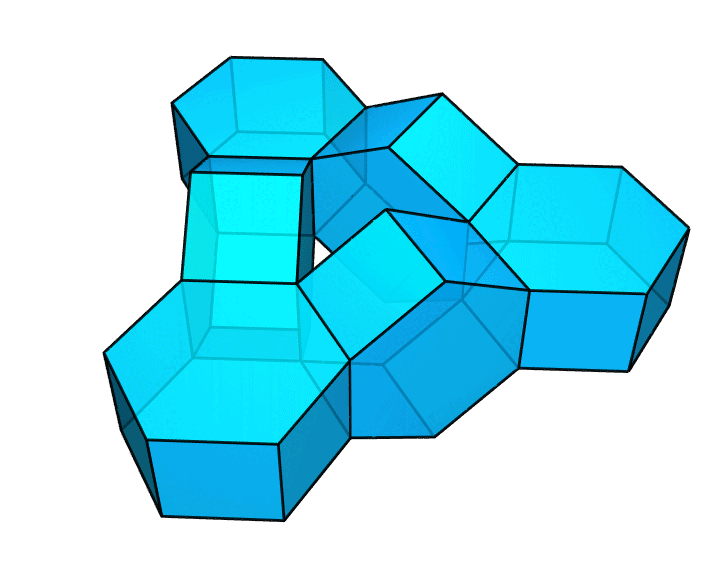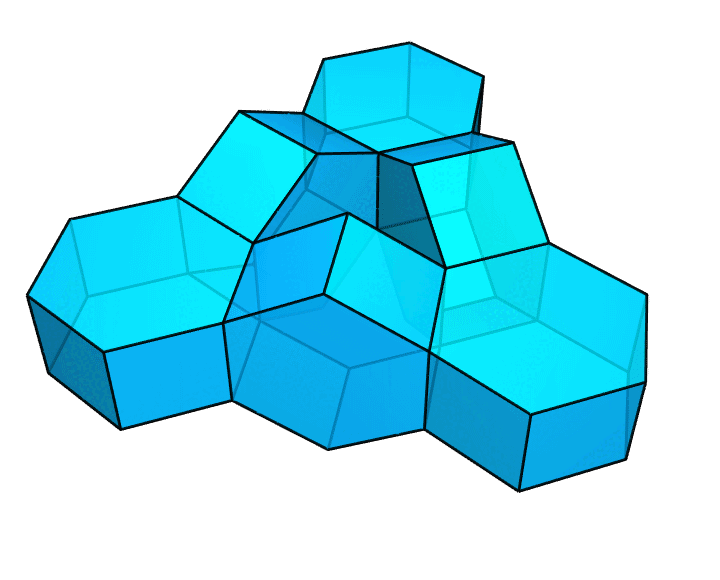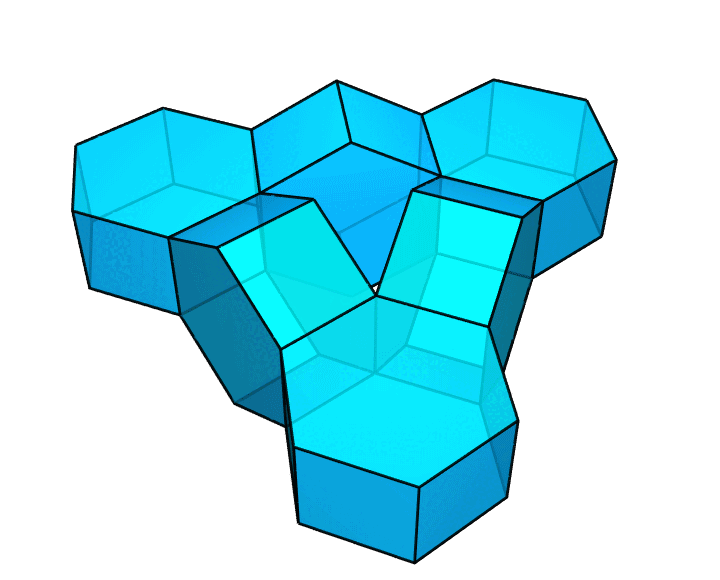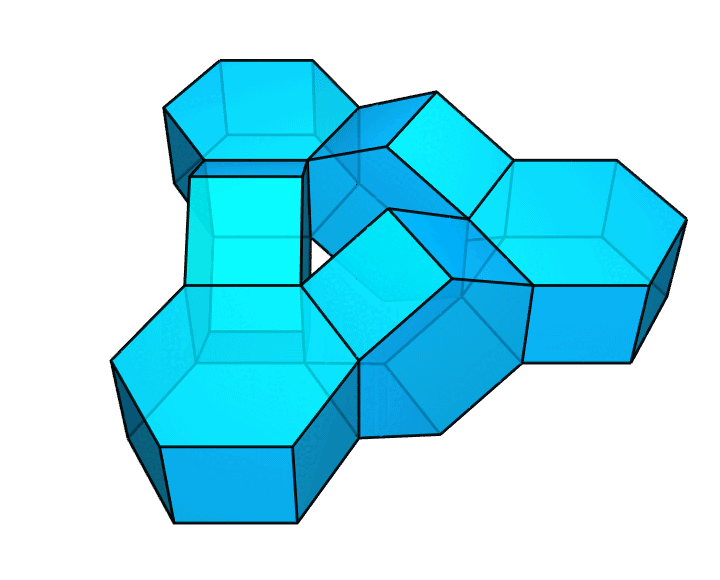
你可以利用这种方式,构造出一些更大胆、更疯狂的图形。比方说,像下图这样,把这些正六棱柱连成一个纽结。
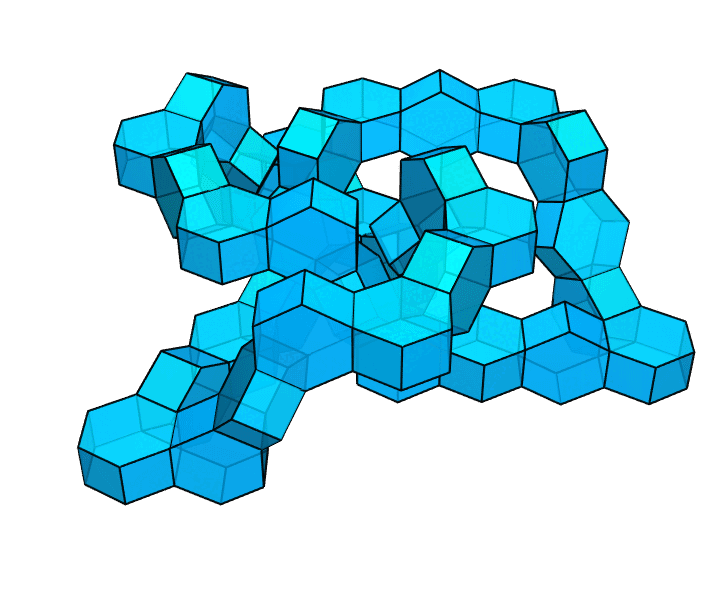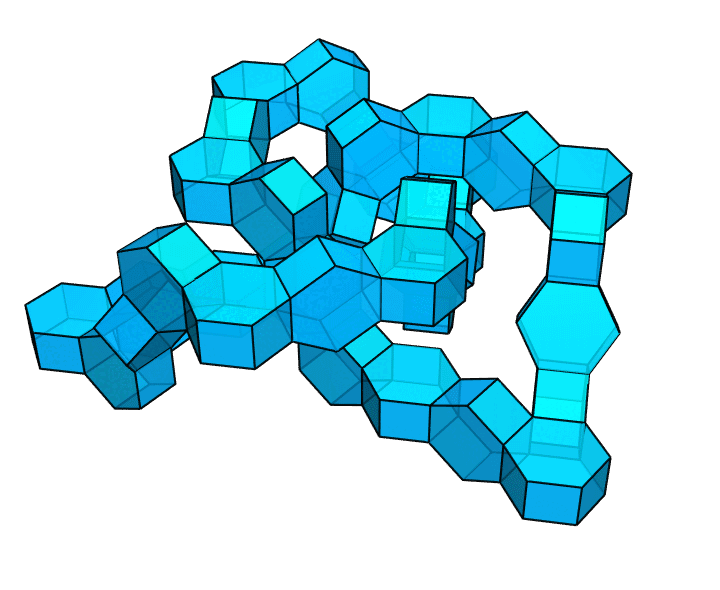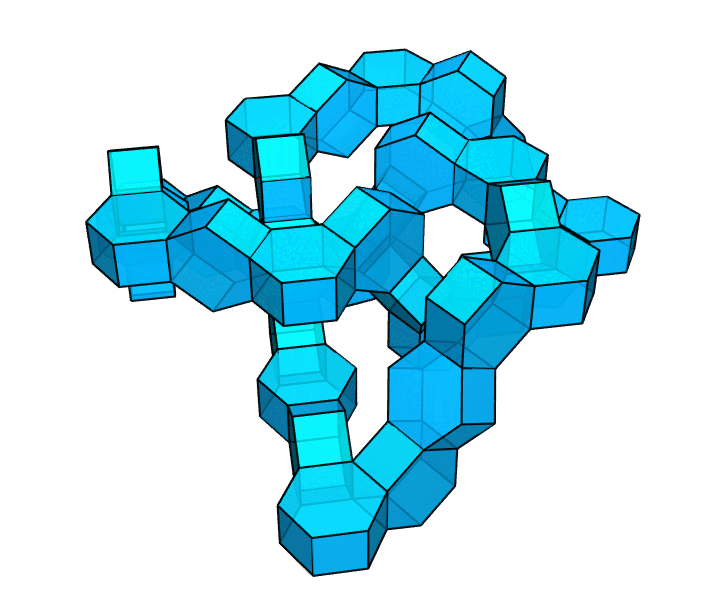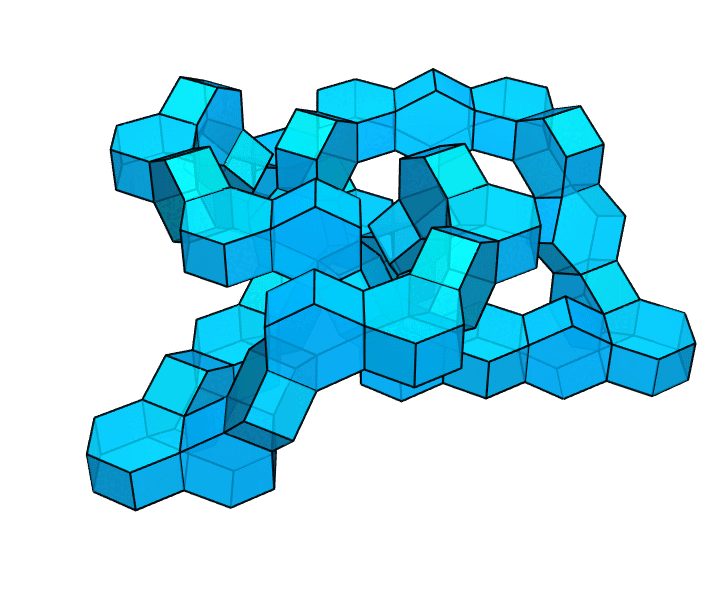
呃……这还算环面多面体吗?换句话说,这还算只有 1 个洞的多面体吗?是的,还算。一个多面体有几个洞,就意味着为了保证它仍然连通,最多能切几刀(每一刀都要切出一个完整的断面)。这是对洞的个数的一种更有效的刻画方式。上图中,只切一刀,整个图形有可能是仍然连通的(比如把链条中的某处切断),也有可能被分成两部分(比如像用削皮刀一样削下表面的一块皮)。但是,如果切两刀,整个图形必然不再连通。这说明,该多面体确实属于只有 1 个洞的多面体。它是环面多面体。
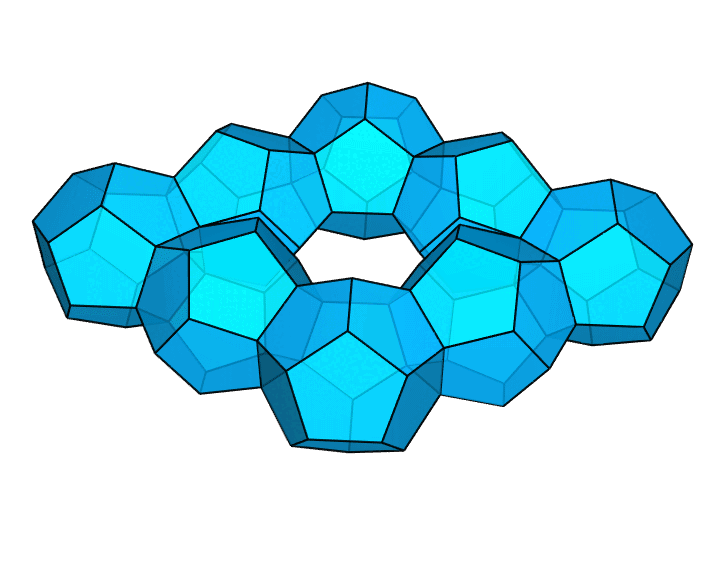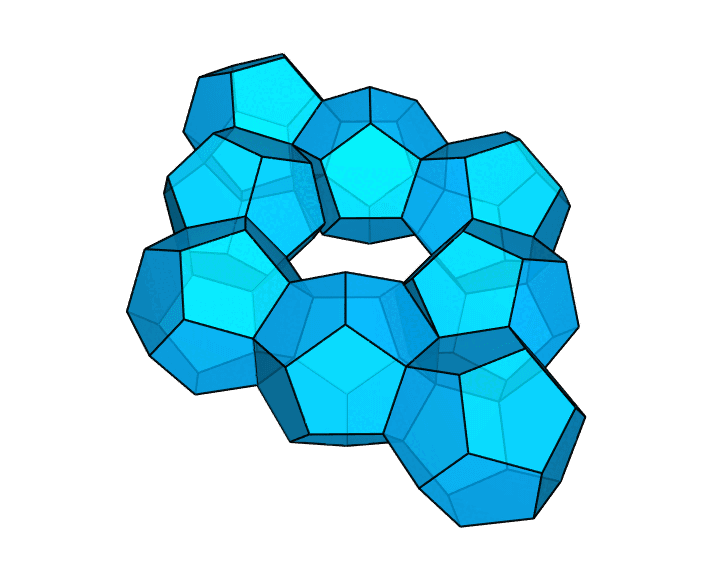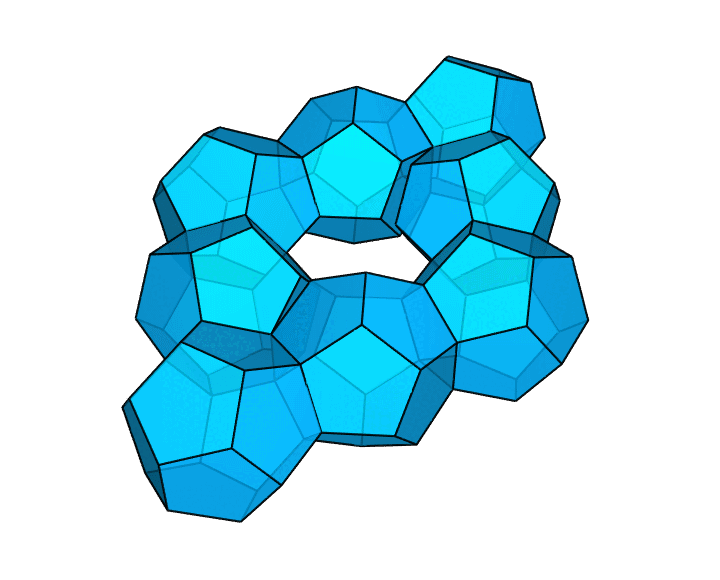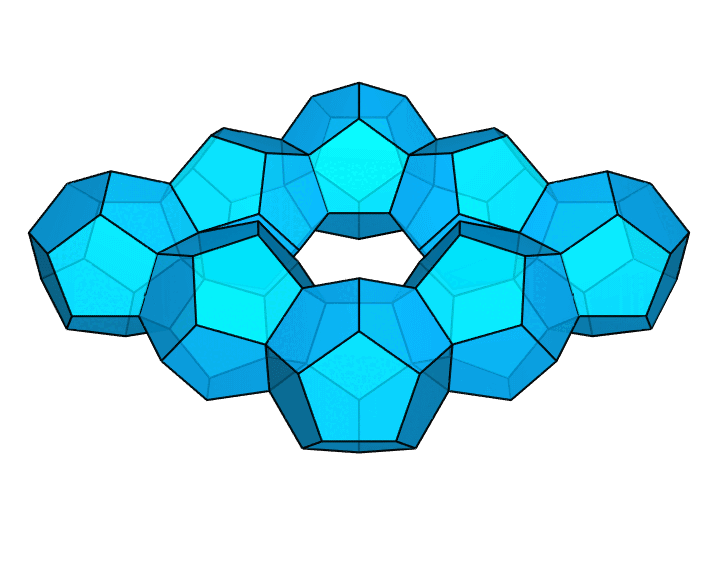
想要看更帅的吗?这是用 8 个正十二面体拼成的环面多面体。显然,它也满足,每个面都是正多边形。
构造所有面均为正多边形的环面多面体还有很多别的截然不同的方式。下面这一对凸多面体具有很有趣的性质:
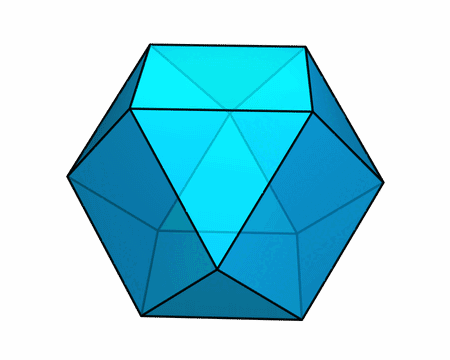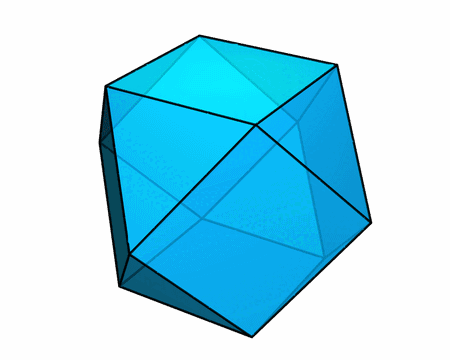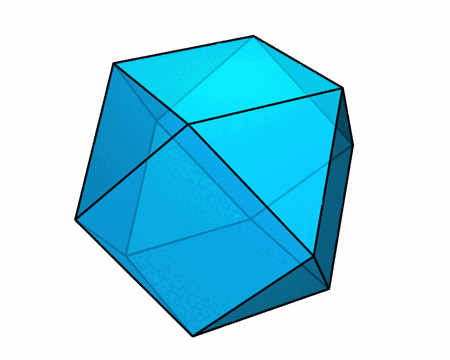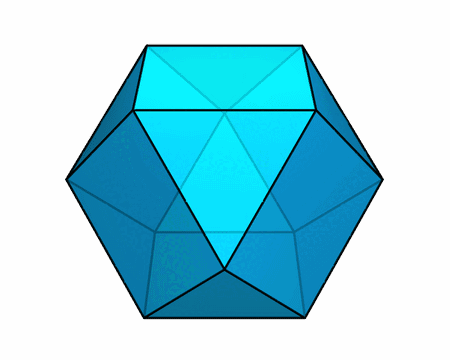
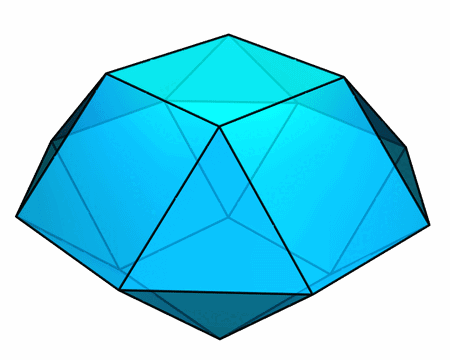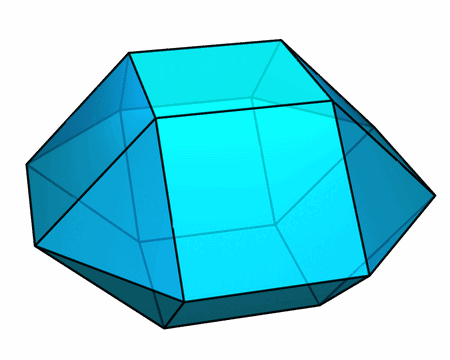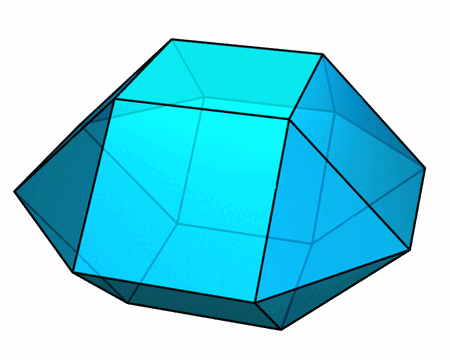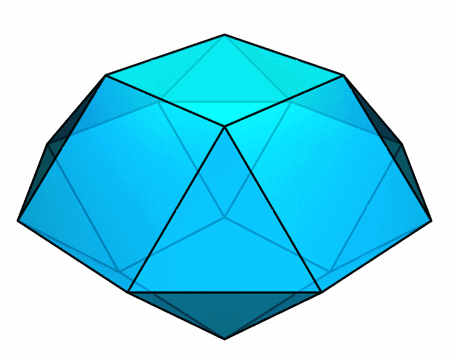
- 它们的每个面都是正多边形
- 它们的高度相同(都是棱长的 √2 倍)
- 它们的顶面完全相同,底面也完全相同
- 重叠放置后,前者完全位于后者内部
我们就能在后者当中挖出一个形如前者的孔。这就又得到了一个满足要求的环面多面体。
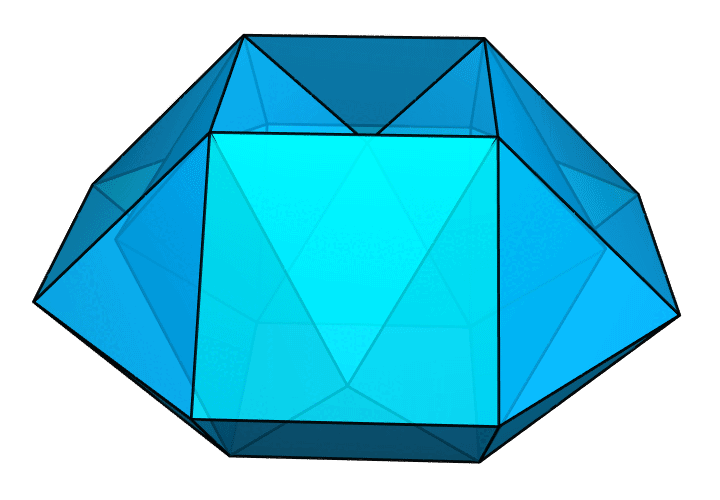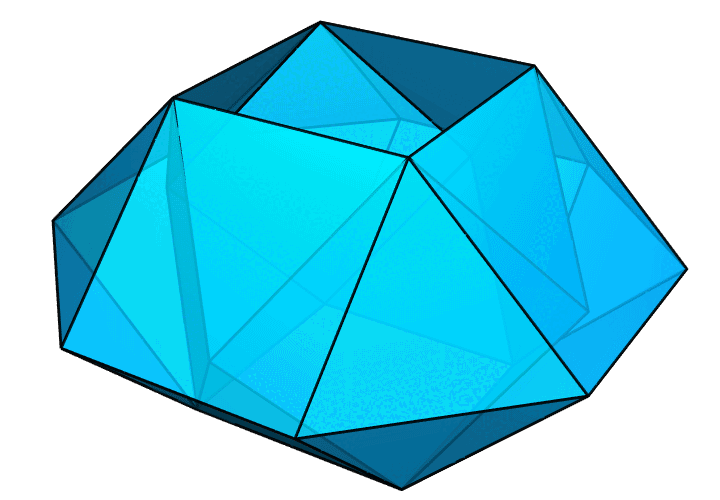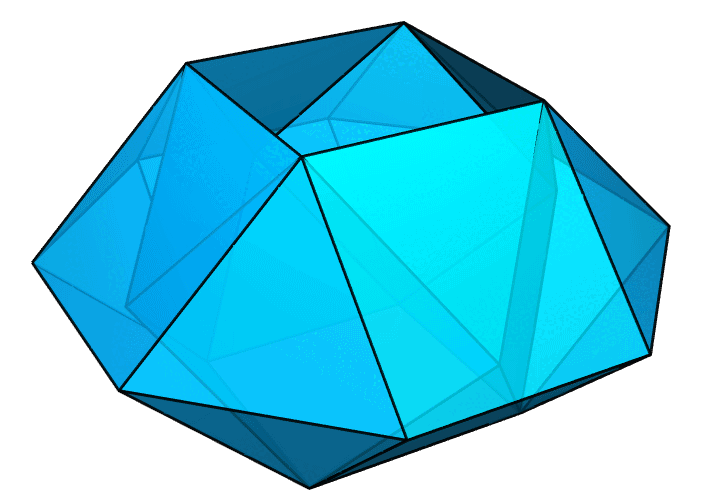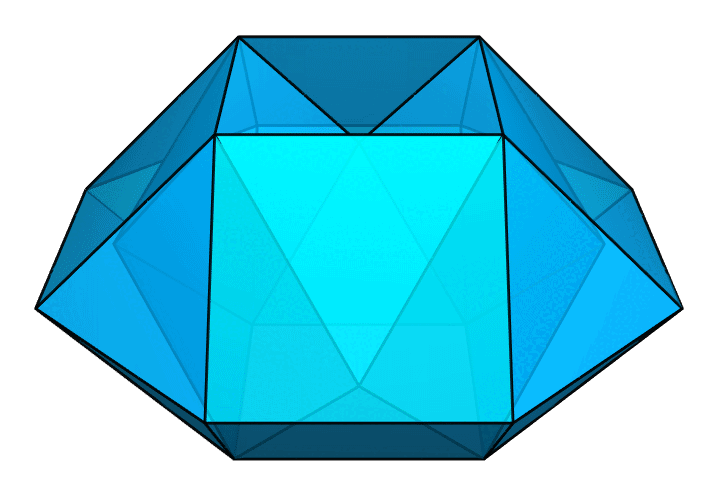
下面是一个更加复杂的例子。中间的孔是一个侧立着的正十棱柱。
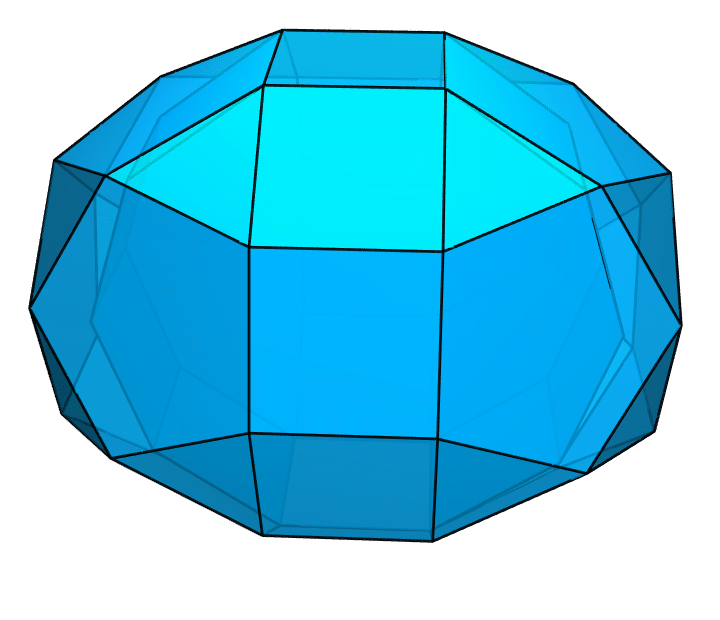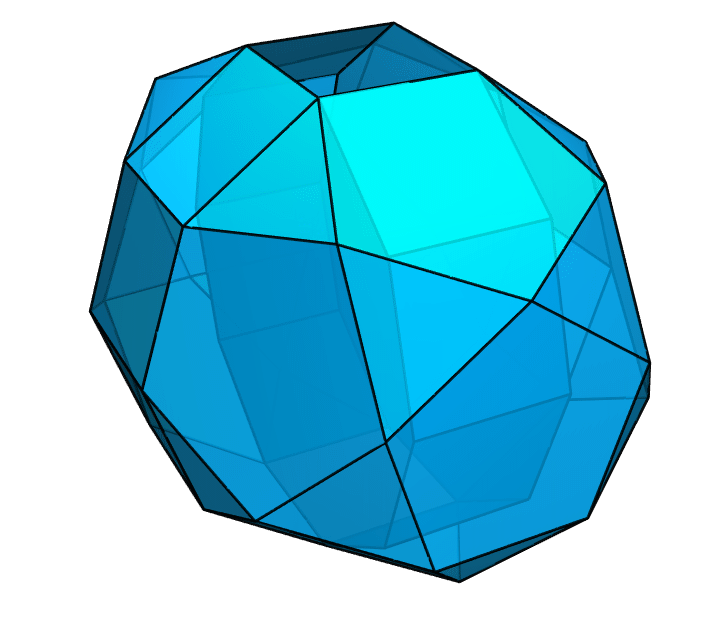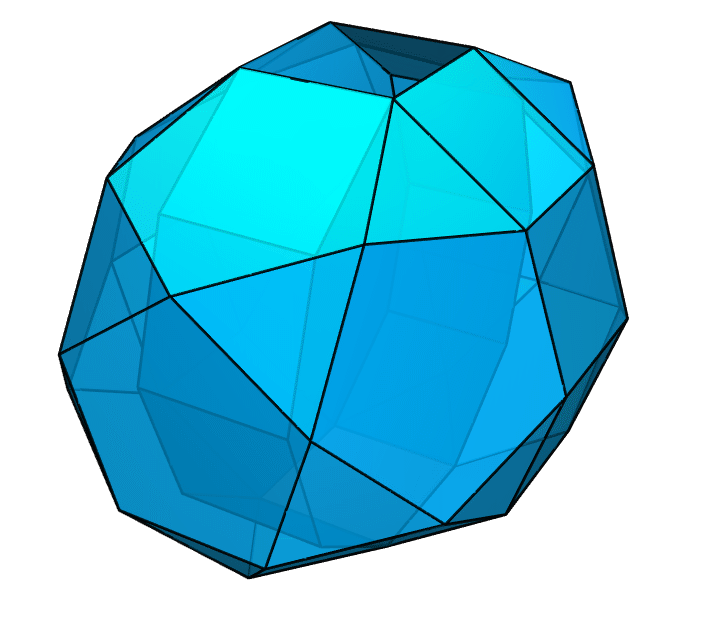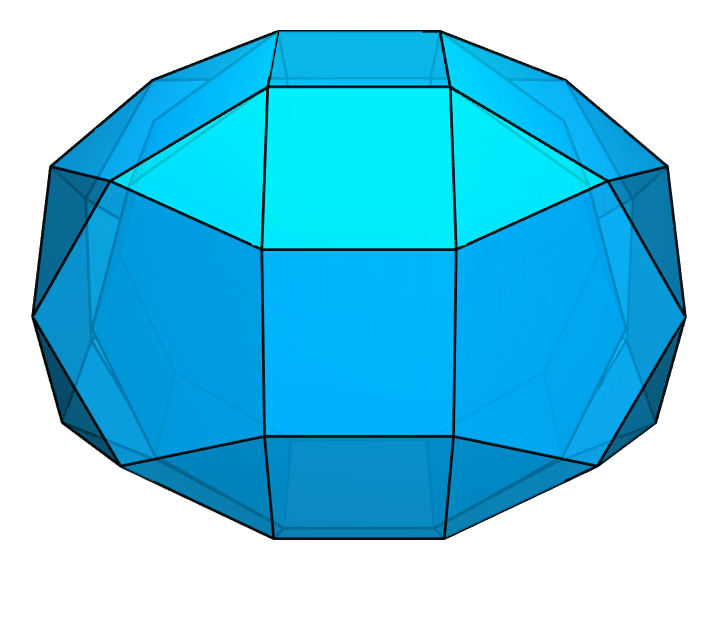
Bonnie Stewart 对这样的多面体进行了非常细致的研究,并写成了 Adventures Among the Toroids 一书。这样的多面体也就有了一个名字,叫作 Stewart 多面体。
任意两个面之间都有一条公共棱
在空间中,四面体有一个相当独特的性质:任意两个面之间都有恰好一条公共棱。你相信吗,除了四面体以外,还有别的多面体也满足这个性质!
Leonhard Euler 发现,如果把多面体的顶点数、棱数、面数分别记作 V、E、F,那么 V − E + F = 2 始终成立。例如,正方体的顶点数、棱数、面数依次为 8、12、6,满足 8 − 12 + 6 = 2;正十二面体的顶点数、棱数、面数依次为 20、30、12,满足 20 − 30 + 12 = 2;n 棱柱的顶点数、棱数、面数依次为 2n、3n、n+2,仍然满足 2n − 3n + (n+2) = 2。如果一个多面体的任意两个面之间都有且仅有一条棱,棱的数量就应该满足 E = F · (F − 1) / 2。显然,这个多面体的每个顶点都只能引出三条棱(否则就会出现一对不符合要求的面),所以总的棱数似乎等于 3V。但用这样的方法统计棱数,每条棱都被重复计算了一次,所以真实的等式应该是 E = 3V / 2。结合 V − E + F = 2,我们就得到了关于 V、E、F 的三个等量关系。它有两组解:V = 2、E = 3、F = 3,以及 V = 4、E = 6、F = 4。前一组解显然不是多面体。后一组解就是四面体。
那……为什么刚才我们说,还有别的多面体也满足,任意两个面之间都有恰好一条公共棱呢?这是因为,这个多面体其实不见得满足 V − E + F = 2。如果它是环面多面体,V、E、F 之间的关系就要修正为 V − E + F = 0。你可以这样来理解:如果一个多面体上有两只“手臂”,“手臂”末端是全等的 n 边形,把它们粘合在一起,就会形成一个环面多面体;这个操作会让顶点数减少 n,棱数减少 n,面数减少 2,所以原来 V − E + F 等于 2,现在 V − E + F 就该等于 0 了。
联立 E = F · (F − 1) / 2、E = 3V / 2、V − E + F = 0,再次得到两组解:V = 0、E = 0、F = 0,以及 V = 14、E = 21、F = 7。前一组解显然不是多面体。后一组解是否对应着某个真实存在的多面体呢?1977 年,Lajos Szilassi 发现了这样的多面体,如下图所示。它就是 Szilassi 多面体。它的每个面都有 6 条边,正好跟其余的 6 个面各接触一次。由于它的 7 个面两两相邻,这就立即说明了,在环面上给任意地图染色,使得相邻区域颜色不相同,存在着至少需要 7 种颜色的情况。

除了四面体和 Szilassi 多面体以外,还有没有别的多面体也满足任意两个面之间都有一条公共棱呢?如果有这样的多面体,那它必须得有比环面多面体更多的洞才行。每多一个洞,V − E + F 的值就会继续减 2,我们就能得到关于 V、E、F 的各种新的解。下一个有正整数解的情况发生在有 6 个洞的时候,此时 V = 44,E = 66,F = 12。但是,目前人们还不知道这能不能在三维空间中实现出来。事实上,除了四面体和 Szilassi 多面体以外,人们还没找到任何一个满足要求的新多面体,也没证明这样的多面体就不存在了。这是一个数学未解之谜。
任意两个顶点之间都有一条棱相连
在空间中,四面体有一个相当独特的性质:任意两个顶点之间都有一条棱。你相信吗,除了四面体以外,还有别的多面体也满足这个性质!
由于任意两点之间都有一条棱,因此这样的多面体满足 E = V · (V − 1) / 2。另外,这个多面体的每个面肯定都是三角形,所以总的棱数似乎等于 3F。但用这样的方法统计棱数,每条棱都被重复计算了一次,所以真实的等式应该是 E = 3F / 2。结合 V − E + F = 2,我们就得到了关于 V、E、F 的三个等量关系。它有两组解:V = 3、E = 3、F = 2,以及 V = 4、E = 6、F = 4。前一组解显然不是多面体。后一组解就是四面体。
为了获得一些新的可能性,我们试着考虑一下环面多面体。这样一来,V − E + F = 2 就要换成 V − E + F = 0。这会得到两组新的解:V = 0、E = 0、F = 0,以及 V = 7、E = 21、F = 14。前一组解显然不是多面体。后一组解真的能被实现出来,如下图所示。它就是 Császár 多面体。它是 Ákos Császár 在 1949 年发现的。Ákos Császár 称它为“没有对角线的多面体”。

这个多面体的面数较多,内部比较混乱。我额外做了一个动图,一步一步地展示这个多面体是怎么搭建起来的。这样的话,大家应该就能比较容易地看出,它确实是一个环面多面体,并且任意两点之间确实都有一条棱。

容易看出,上面这两个小节提出的问题存在着对偶关系。也就是说,如果交换顶点和面的地位,对问题中的元素作这样的变换:
- 顶点数 ↔ 面数
- 两个顶点之间有一条棱 ↔ 两个面之间有一条棱
- 顶点处引出的棱数 ↔ 面周围一圈的棱数
其中一个问题就会变成另外一个问题。事实上,Szilassi 多面体和 Császár 多面体也是一对对偶多面体。Szilassi 多面体的每个面,都对应着 Császár 多面体的一个顶点;Szilassi 多面体的每个顶点,也都对应着 Császár 多面体的一个面。
同样地,除了四面体和 Császár 多面体以外,人们还没找到别的也满足任意两点之间都有棱的多面体,也没证明这样的多面体就不存在了。
由全等的面构成的环面多面体
正四面体、正六面体、正八面体、正十二面体、正二十面体、由两个全等的 n 棱锥拼合而成的双 n 角锥等等,都是由全等的面构成的多面体。能不能用全等的面做出一个环面多面体呢?
其实,最开始在研究由正多边形构成的环面多面体时,有些环面多面体用的就已经是全等的面了。比如那个用正方体拼成的环面多面体,和那个用正十二面体拼成的环面多面体。但是,它们的面数有些多。能不能让面数更少一些呢?
很多人或许会立即想到一些看上去非常有希望的方案,比如像下图这样的画框形环面多面体。这样的方案是不可行的。容易看出,四周的侧面确实是规整的矩形,但中间的几个向内倾斜的面其实是梯形。导致这一现象的原因,就是环面多面体的内圈比外圈更短。很多其他类似的方案也都会因为这一点而失效。怎么办呢?
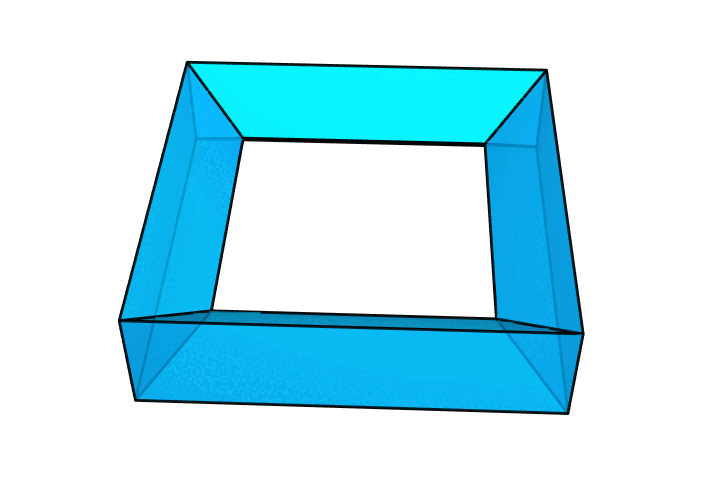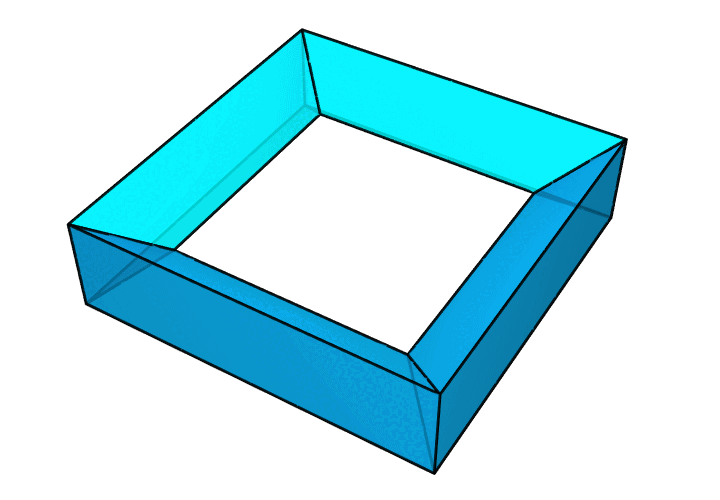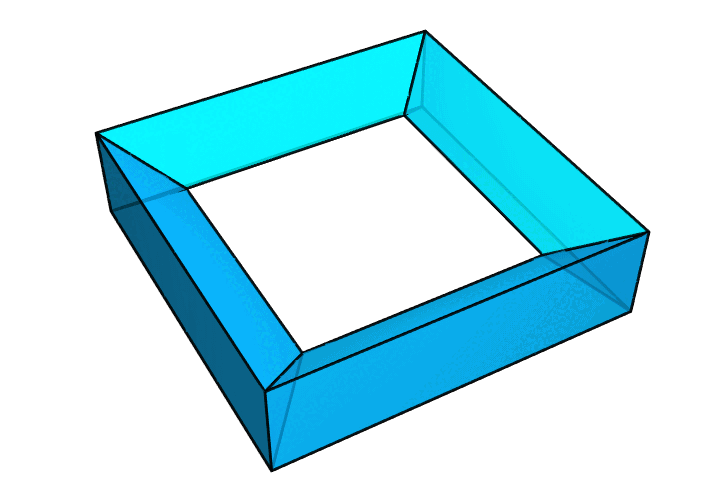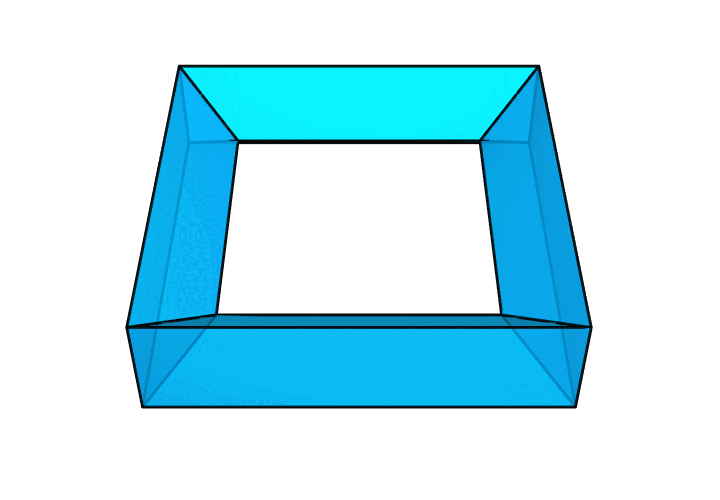
Lajos Szilassi,也就是提出 Szilassi 多面体的那个人,给出了一个满足要求的 24 面体,如下图所示。为了方便大家看到内部结构,我把外圈做成了时隐时现的样子。
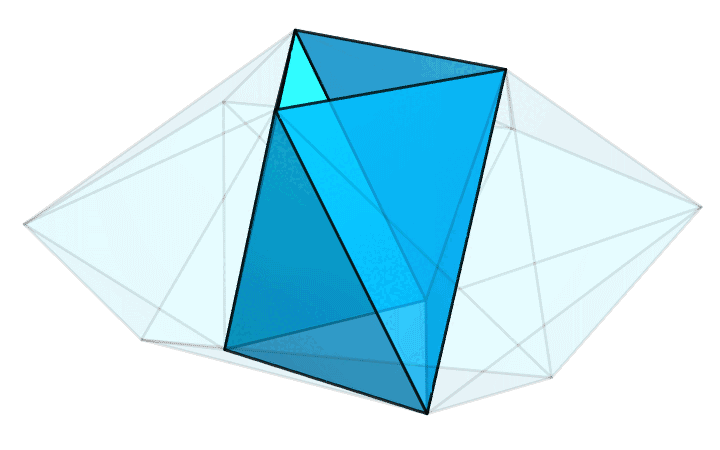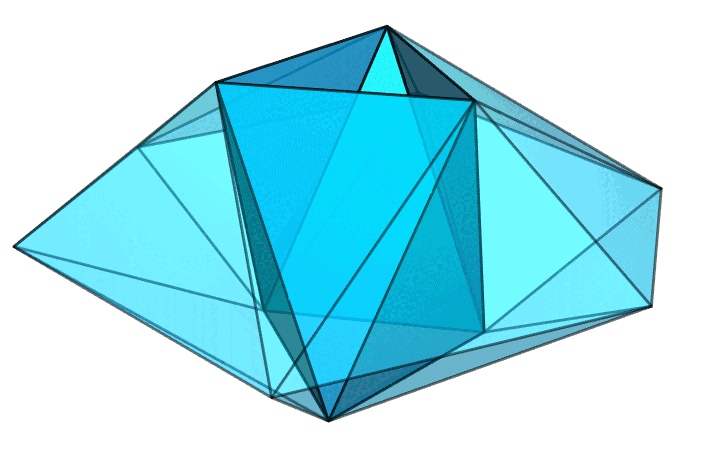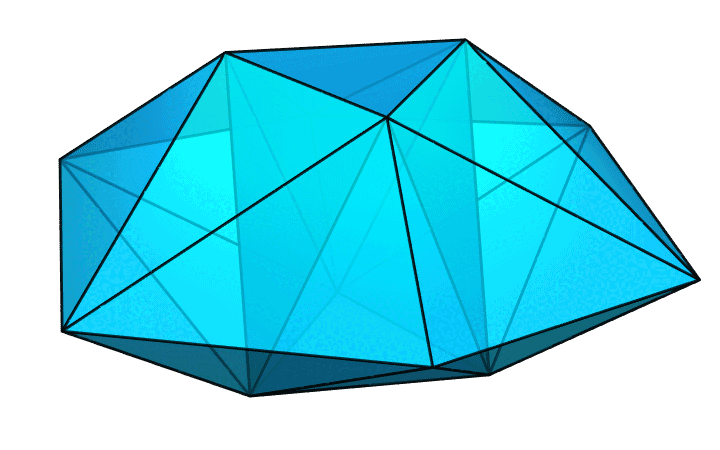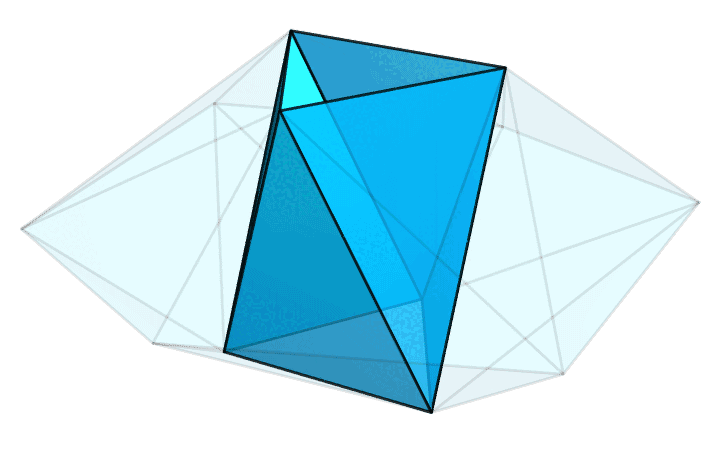
整个多面体就好像一个打了孔的飞碟。这个孔是由 6 个等腰三角形构成的,它们一上一下相间摆放,形成了一个圈。飞碟的边沿是由等腰三角形的腰组成的。值得注意的是,边沿上的 6 个顶点并不在同一水平面上,它们的高度是上下交错着的。其中 3 个顶点对着的是上方三角形孔的边和下方三角形孔的角,另外 3 个顶点对着的则是上方三角形孔的角和下方三角形孔的边。
根据我目前查到的资料来看,在所有由全等的面构成的环面多面体中,这是目前已知的面数最少的。
棱数最少的环面多面体
面数最少的环面多面体就是 Szilassi 多面体,它只有 7 个面。顶点数最少的环面多面体就是 Császár 多面体,它只有 7 个顶点。棱数最少的环面多面体呢?Szilassi 多面体和 Császár 多面体都有 21 条棱,但这并不是棱数最少的情况。我们能够很容易构造出棱数更少的情况,例如下面这个三角形画框。它有 9 个面,每个面都是四边形。它有 9 个顶点,每个顶点都引出了 4 条棱。它只有 18 条棱。
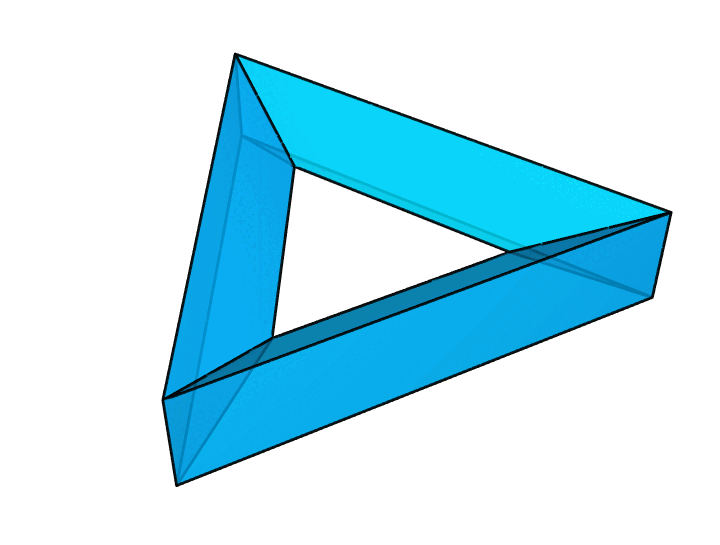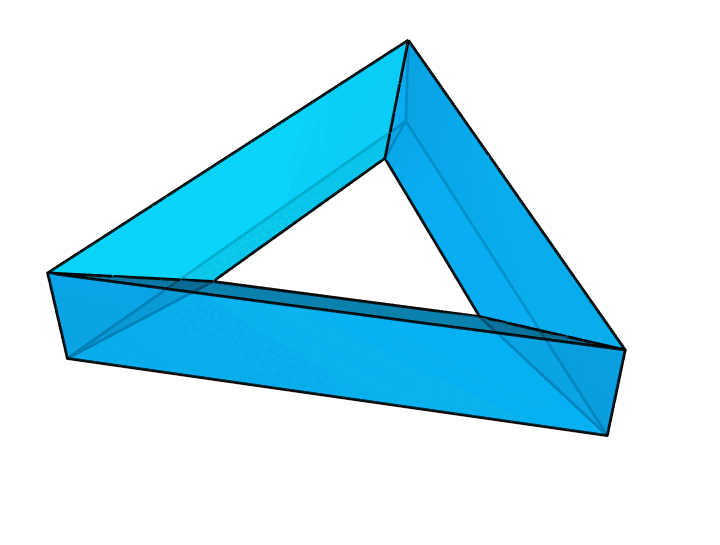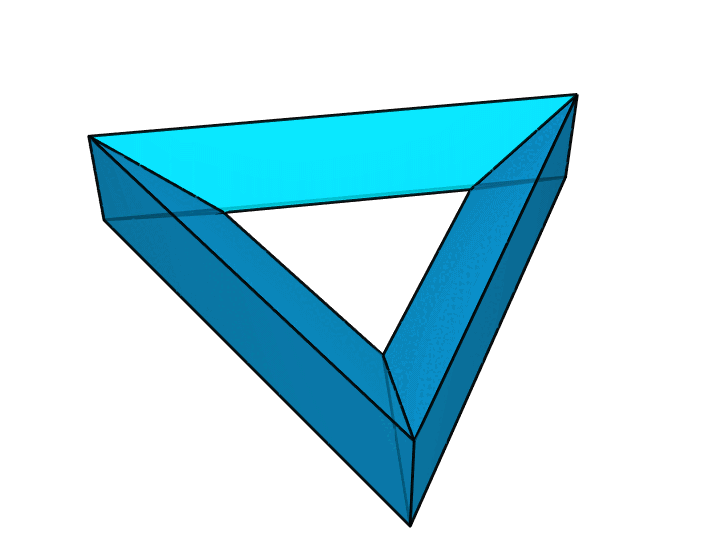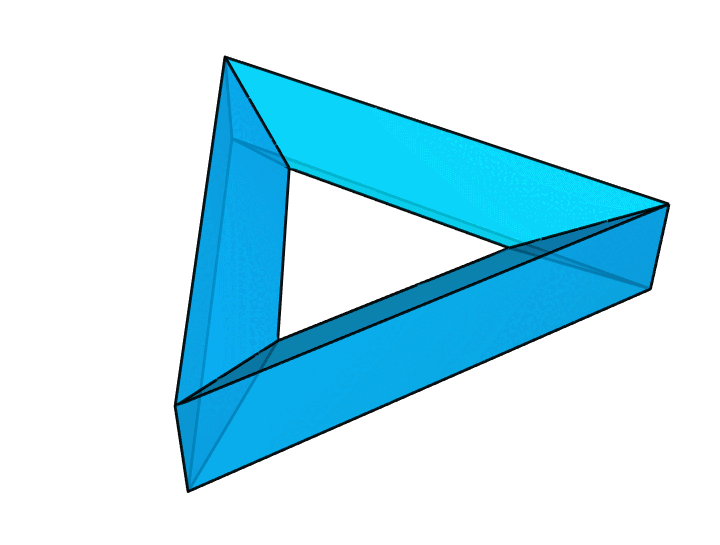
可以证明,这就是棱数最少的情况。当然,我们也可以把上图做成很多别的样子,比如下图这样。它们的本质是相同的。
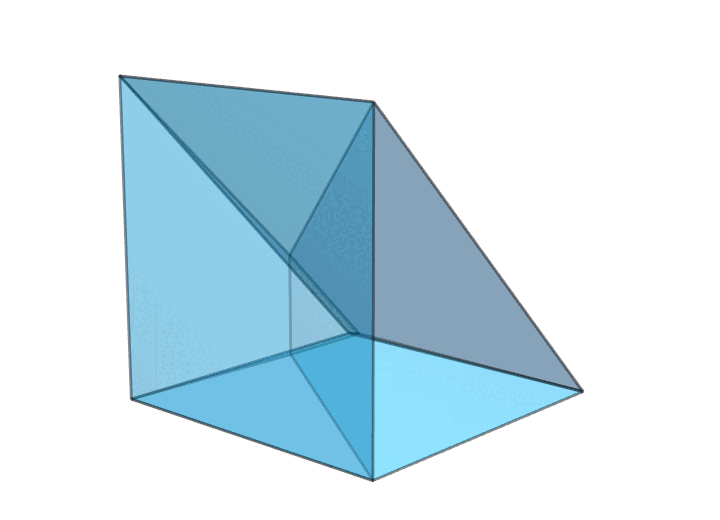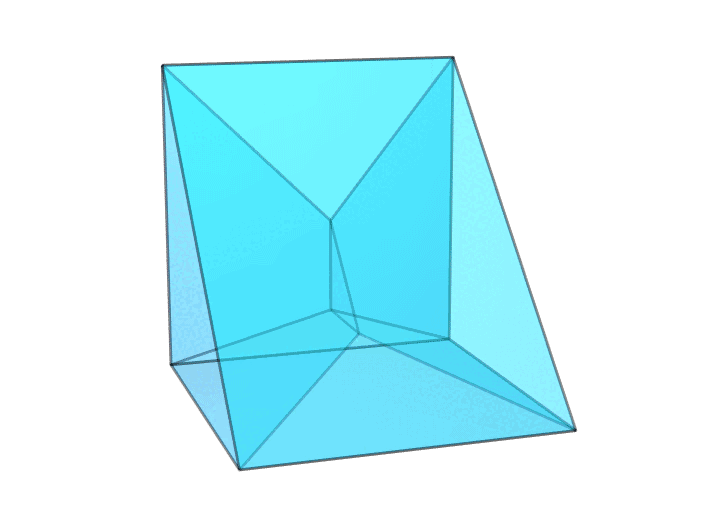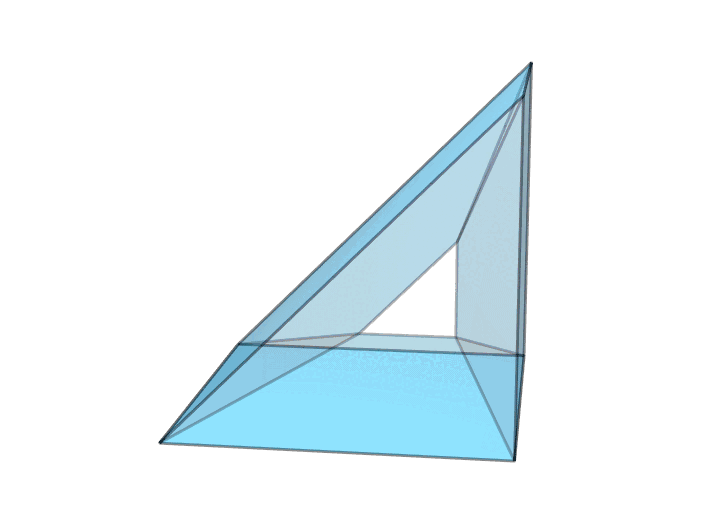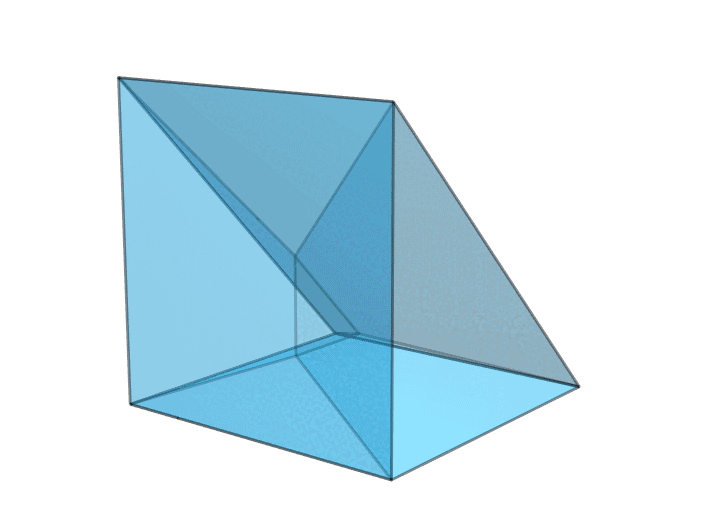
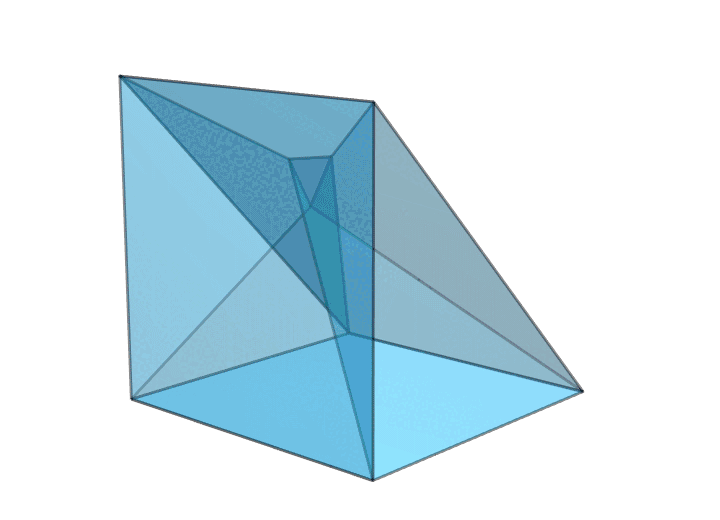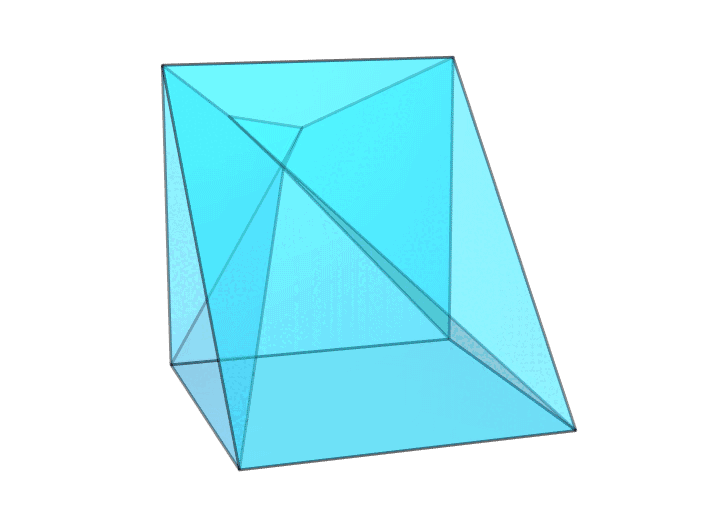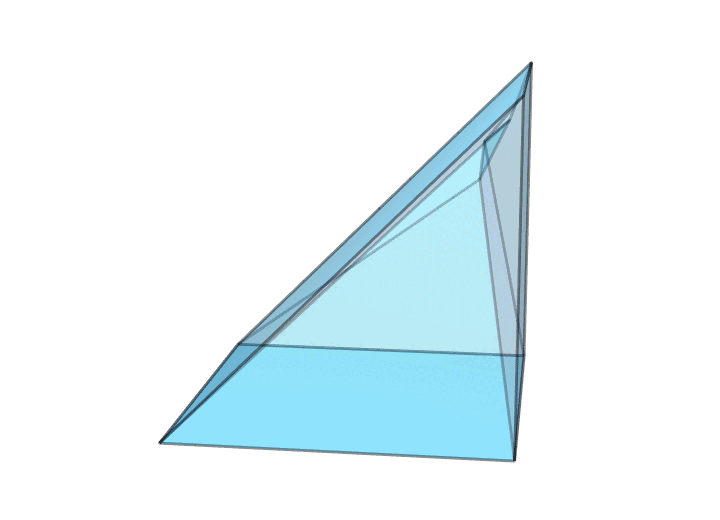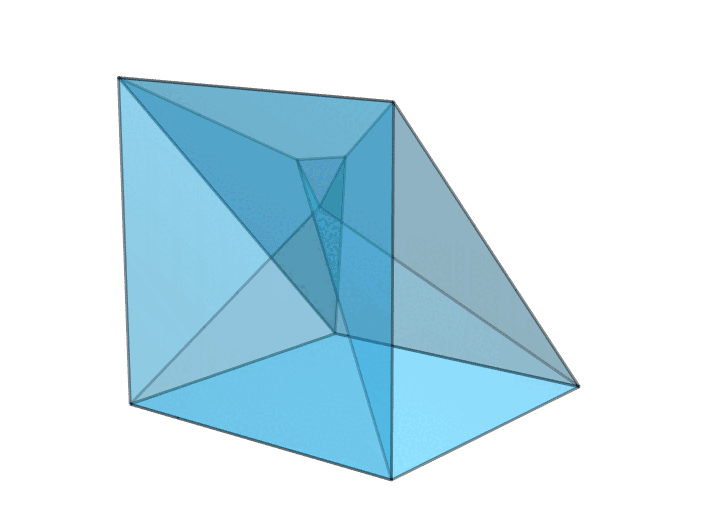
有趣的是,要想让环面多面体只有 18 条棱,还有另外一种本质不同的方案——扭转过的三角形画框,如下图所示。对比上图中每一对红色面的位置和下图中每一对红色面的位置,你就知道为什么把它叫作扭转过的三角形画框了。
如果你喜欢这篇文章,你或许会喜欢我以前写的另一篇文章:高度对称的多面体和它们的对偶多面体。
本文很多图片的制作借用了 Alex Doskey 的数据,在此表示感谢。