2009-10-27 0:55| 
14 Comments | 本文内容遵从在今天晚上的微观经济学课上，我又听到了一个比较有意思的东西。试着找找各种类型的连续函数f(x)，画出f'(x)和f(x)/x的函数图像，你会发现一个奇怪的现象：f'(x)与f(x)/x相交的地方都是f(x)/x取到极值的地方。简单地算一算，我们不难证实这个结论。f(x)/x的导数等于f'(x)/x - f(x)/x^2。将f'(x)=f(x)/x代入上式，可得f'(x)/x - f(x)/x^2 = f(x)/x^2 - f(x)/x^2 = 0。这就是说，当f'(x)与f(x)/x相等的时候，f(x)/x的导数一定等于0。有意思的是，这个结论还有一个非常直观的解释，你能想到吗？
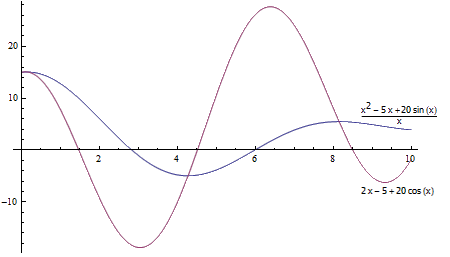
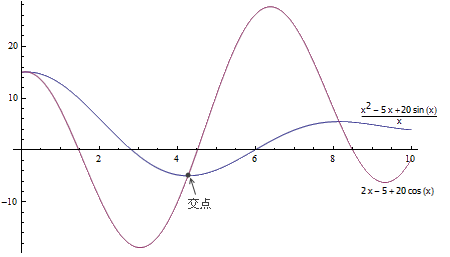
把f(x)看作一个时间-位置函数，那么f(x)/x就表示前x个单位的时间内物体的平均速度，而f'(x)则表示物体在x时刻的瞬时速度。考虑这两个函数的交点，不妨假设在交点左边有f'(x) < f(x)/x，那么在交点右边就一定有f'(x) > f(x)/x。显然，如果当前的速度比平均速度要小，那么平均速度会被拖慢，也即f(x)/x是递减的；反过来，当前的瞬时速度大于平均速度时会向上拉动平均速度，f(x)/x将会变得递增。这就告诉我们，两条曲线的交点处于f(x)/x的极小点。
注意，不管是前面的数学论证还是这里的直观解释，我们都忽略了很多特殊的情况没有讨论，仅仅说明了一些主要思想。不过，这已经足以推出一个重要的经济学结论：边际成本曲线与平均成本曲线相交于后者的最低点。
sf...
Matrix67画图，用的什么工具？
想到了股票分时线和均价线的关系
牛~
学经济学的路过。
有想法写出来就很好~~~加油
果然~
我觉得这是mathematica得作图风格。
我也觉得是，风格很像似
图用 mathematica画的吧
楼上网页中的google广告竟然有一个指向自己分站的页面。。。
orz 自我指涉吧
我是不懂经济的小菜
所以 更喜欢物理意义上的解释
任何规律都遵循物理规律。就像天是大宇宙，人是小宇宙一样。
x=x0 f(x)/x-f'(x)=0
[f(x)/x]'=0 => x=x0
想到方程数值解的牛顿法