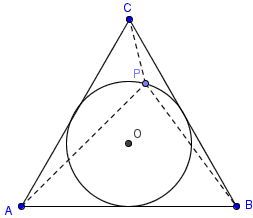
如图，等边三角形ABC，P为三角形内接圆上一点。求证，AP^2 + BP^2 + CP^2为常数。

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 

证明：把整个图形放在三维空间里，其中A=(1,0,0)，B=(0,1,0)，C=(0,0,1)。因此，三角形ABC位于平面x+y+z=1上。图中的内接圆即为某个以原点为球心的球x^2 + y^2 + z^2 = r与该平面相交所得（其中r是某个常数）。于是，我们有

   AP^2 + BP^2 + CP^2
= (1-x)^2 + y^2 + z^2 +
   x^2 + (1-y)^2 + z^2 +
   x^2 + y^2 + (1-z)^2
= 3·(x^2 + y^2 + z^2) – 2·(x + y + z) + 3
= 3·r – 2 + 3
= 常数

来源：http://www.cut-the-knot.org/pythagoras/EquiIn3D.shtml
查看更多：几个把平面几何问题的辅助线做到空间去的数学趣题