下面这个趣题出自 Using your Head is Permitted 谜题站 2016 年 8 月的题目，稍有改动。
屋子里有若干个人，任意两个人都有恰好 1 个共同的朋友。这有可能吗？有可能。比方说，屋子里有 9 个人，其中 8 个人正好组成 4 对朋友，第 9 个人则和前面 8 个人都是朋友。容易验证，任意两个人都有恰好 1 个共同的朋友。我们可以用下面这个图表示此时这 9 个人之间的朋友关系，其中每个点代表一个人，如果两个人是朋友，就在他们之间连一条线。
除了上图展示的情况之外，我们还能构造出很多别的同样满足要求的情况。事实上，上述方案可以扩展到一切奇数个人的情况，比如下面这样：
无穷多个相同大小的正方形格子排成一排，向左右两边无限地延伸。每个格子里都有 0 个、 1 个或多个原子。每一次，你可以对它们做下面两种操作之一：
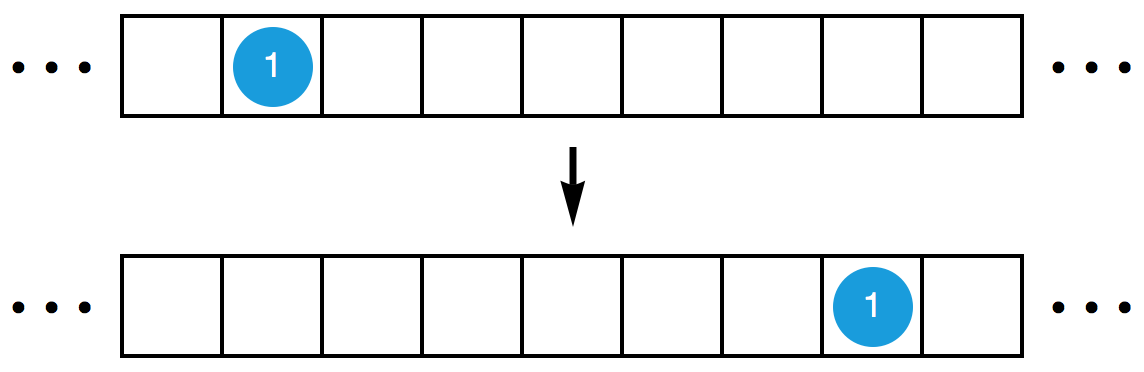
初始时，某个格子里有 1 个原子。现在，你需要在若干次操作之后，让它右移 6 格。也就是说，你需要用若干次操作把下面的第一个图变成第二个图（其中，数字 1 表示该格内的原子数为 1 ）。继续阅读下去之前，你不妨自己先试一试。你可以在纸上画好格子，用硬币、大米、巧克力豆等物体代替原子。
让我们来玩一个游戏。把某个国际象棋棋子放在棋盘上，两人遵循棋子的走法，轮流移动棋子，但只能将棋子往左方、下方或者左下方移动。谁先将棋子移动到棋盘的最左下角，谁就获胜。如果把棋子放在如图所示的位置，那么你愿意先走还是后走？显然，答案与我们放的是什么棋子有关。
这个游戏对于兵来说是没有意义的。在如图所示的地方放马或者放象，不管怎样都无法把它移动到棋盘的最左下角，所以我们也就不分析了。因此，我们只需要研究王、后、车三种情况。
你的数学直觉怎么样？你能凭借直觉，迅速地判断出谁的概率大，谁的概率小吗？下面就是 26 个这样的问题。如果你感兴趣的话，你可以先扫一遍所有的问题，再逐一阅读答案，看看你猜对了多少。这篇文章很长，你可以考虑把它加入书签，每天看几个问题。
1．A 、 B 、 C 、 D 四人玩扑克牌游戏， A 、 C 两人同盟， B 、 D 两人同盟。将除去大小王的 52 张牌随机分发给四人（每人获得 13 张牌）后，下面哪种情况的可能性更大一些？
A．A 、 C 两人手中都没有梅花
B．A 、 C 两人手中囊括了所有的梅花
C．上述两种情况的出现概率相同
A 、 C 两人手中都没有梅花，等价于 B 、 D 两人手中囊括了所有的梅花，它的概率与 A 、 C 两人手中囊括所有梅花的概率相同。因此，这个问题的答案显然是 C 。
著名的四色定理（four color theorem）告诉我们，如果一个地图由若干个连通区域构成（没有飞地），那么在给每个区域染色时，为了让相邻区域的颜色不同，最多只需要四种颜色就足够了。不过，这个结论成立有一个条件：整个地图已经事先确定了。如果我们每次只增加一个区域的话呢？具体地说，如果每次你给一个区域染色之后，我再画出下一个区域，并且之前已经染好颜色的区域不能再修改了，那么四种颜色还足够吗？这里，我们假设，在染色时，你总是遵循一个非常朴素的贪心策略：用第一个合法的颜色给每个新的区域染色。下面这个例子告诉我们，在这些假设下，四种颜色就不够了，有时五种颜色是必需的。
我们的问题就是，在这些假设下，五种颜色就一定够吗？有没有可能构造出某个情况，使得六种颜色是必需的？有没有可能构造出某个情况，使得七种颜色是必需的？