无穷多个相同大小的正方形格子排成一排,向左右两边无限地延伸。每个格子里都有 0 个、 1 个或多个原子。每一次,你可以对它们做下面两种操作之一:
- 选择某个格子,保证该格子内至少含有 1 个原子。将该格子内的其中 1 个原子分裂为 2 个,从而使得该格子内的原子数量减 1 ,两边的邻格里的原子数量分别加 1。
- 选择某个格子,保证两边的邻格里均至少含有 1 个原子。从两边的邻格里各取 1 个原子聚合起来,从而使得两边的邻格里的原子数量分别减 1 ,该格子内的原子数量加 1。
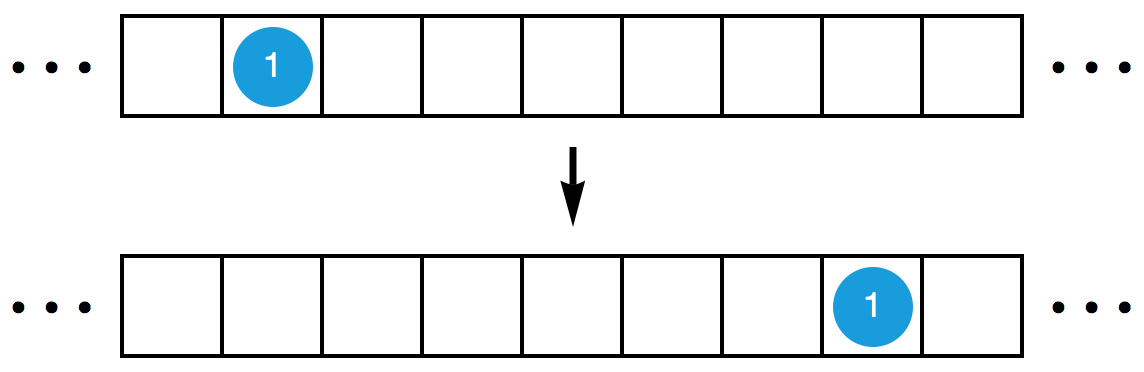
初始时,某个格子里有 1 个原子。现在,你需要在若干次操作之后,让它右移 6 格。也就是说,你需要用若干次操作把下面的第一个图变成第二个图(其中,数字 1 表示该格内的原子数为 1 )。继续阅读下去之前,你不妨自己先试一试。你可以在纸上画好格子,用硬币、大米、巧克力豆等物体代替原子。
其中一种方法如下。

你或许会觉得这里面隐藏着一些规律。我们似乎可以对上面的方法进行扩展,把初始时的那个原子移到它右边的任意一格里,比方说把初始时的那个原子移到它右边第 2 格,或者第 3 格,或者第 7 格的位置。然而,简单地试试,你会发现,这还真的不行。上述方法只适用于右移 6 格的情况。事实上,我们可以证明,如果某个格子里的 1 个原子最终可以变为另外一个格子里的 1 个原子,这两个格子的位置一定相差 6 或者 6 的整倍数。
让我们像下面这样,为每一个格子都赋一个值,其中 ω = (-1)1/3 ,即 -1 在复数范围内的一个立方根。注意到 ω 满足 ω3 + 1 = 0 ,即 (ω + 1)(ω2 – ω + 1) = 0 ;而 ω + 1 ≠ 0 ,于是只能是 ω2 – ω + 1 = 0 。

对于整个棋盘上的任意一种原子排布,我们都可以把每个放有原子的格子里的值加在一起,一个格子里有几个原子,它对应的值就加几次。我们把如此得到的总和叫做此时棋盘上原子排布的特征值。例如,如果 ω-2 上有 2 个原子, ω2 上有 1 个原子, ω3 上有 4 个原子,其他格子都是空的,那么此时棋盘上原子排布的特征值就是 2 · ω-2 + 1 · ω2 + 4 · ω3 。
当位于 ωn 位置上的原子分裂时,特征值会减小一个 ωn ,但会增加一个 ωn-1 和一个 ωn+1 ,所以特征值的变化量为 – ωn + ωn-1 + ωn+1 = ωn-1 · (- ω + 1 + ω2) 。然而,之前我们说过, ω 的取值满足 ω2 – ω + 1 = 0 。因此,任何一次原子分裂操作都不会改变原子排布的特征值。
类似地,原子聚合导致的特征值的变化量为 – ωn-1 – ωn+1 + ωn = ωn-1 · (- 1 – ω2 + ω) = 0 。因此,任何一次原子聚合操作也都不会改变原子排布的特征值。
如果原来整个棋盘上只有 ωn 位置上有 1 个原子,后来变得整个棋盘上只有 ωm 位置上有 1 个原子,这就意味着 ωn = ωm ,即 ωm / ωn = 1 ,即 ωm-n = 1 。考虑到 ω = (-1)1/3 ,因此为了让 ωm-n = 1 ,只有可能 m – n 是 6 的整倍数。这就解答了前面提出的问题。
我最初是在这里看见的这个问题: http://blog.sigfpe.com/2007/09/arboreal-isomorphisms-from-nuclear.html 。如果你对这个问题感兴趣的话,你一定会喜欢下面这个类似的但是更经典、更精彩的问题: http://www.matrix67.com/blog/archives/4595 。