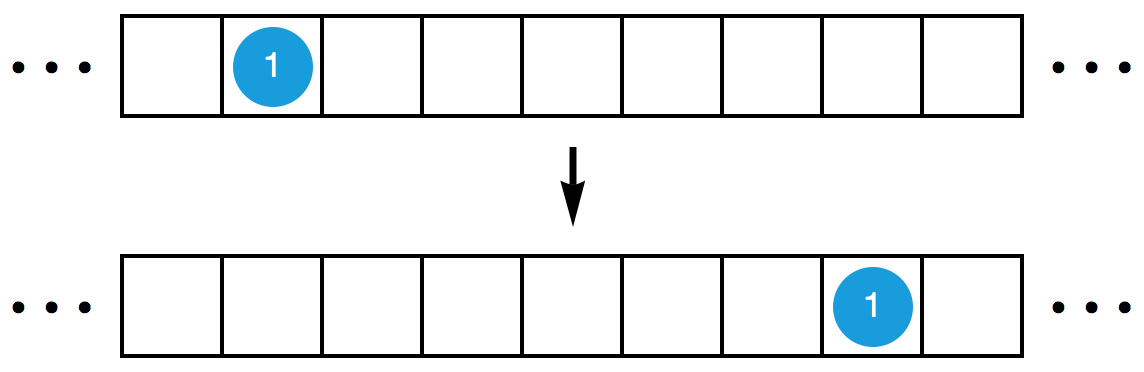
无穷多个相同大小的正方形格子排成一排，向左右两边无限地延伸。每个格子里都有 0 个、 1 个或多个原子。每一次，你可以对它们做下面两种操作之一：
初始时，某个格子里有 1 个原子。现在，你需要在若干次操作之后，让它右移 6 格。也就是说，你需要用若干次操作把下面的第一个图变成第二个图（其中，数字 1 表示该格内的原子数为 1 ）。继续阅读下去之前，你不妨自己先试一试。你可以在纸上画好格子，用硬币、大米、巧克力豆等物体代替原子。
很早以前，我简单介绍过 Julia 集和 Mandelbrot 集，文章在此。这可以说是数学中最神秘、最令人敬畏的研究对象之一。不过，那时我对这个话题了解还不太深。今天见到这个网页，让我对 Julia 集和 Mandelbrot 集有了更深的了解。我查阅了一些其他的资料，然后写下这篇长文，与大家一同分享。继续阅读以前，建议先看看我原来那篇文章（很短），那里面有很多漂亮的 Julia 集和 Mandelbrot 集的图片，这篇文章就不再展示了。
还是让我们先来简单复习一下复数吧。由于承认“负数也能开平方”将会带来很多幽雅和便利的结论，因此我们发明了虚数，用 i 来表示 -1 的平方根（即虚数单位），并把实数扩展为复数（即一切形如 a + b i 的数）。正如实数可以用数轴上的点来表示一样，复数可以用平面直角坐标系上的点来表示。令 x 轴表示复数的实数部分，令 y 轴表示复数的虚数部分，则 a + b i 就对应了平面上的点 (a, b) 。我们把这个平面直角坐标系叫做“复平面”。
大家或许知道 Banach-Tarski 悖论——把一个三维球分成有限多份并重新拼成两个和原来一模一样大的球——这个悖论告诉我们利用选择公理我们能够推出看上去多么不合逻辑的东西。今天我听说了另一个类似的悖论叫做 Sierpinski-Mazurkiewicz 悖论，它的结论在直观上同样令人难以接受，并且推导不依赖于选择公理。
Sierpinski-Mazurkiewicz 悖论是说，存在平面上的一个点集 S ，我们能把它划分成两个子集 A 和 B ，使得 A 旋转 1 弧度后与 S 完全重合， B 平移一个单位后也与 S 完全相同。换句话说，存在这么一个点集，我们能把它分成两个与自身一模一样的子集！这听上去实在是不可思议，然而构造却极其简单。
Dan Christensen发现，把所有次数不超过5的、系数在-4到4范围内的整系数多项式的所有根描绘在同一个复平面上，你会看到一个异常壮观的画面。图中的每个灰色点代表某个二次多项式的一个根，蓝色点代表三次多项式的根，红色代表四次多项式的根，黑色代表五次多项式的根。水平线代表实轴，0和±1的地方有很明显的空洞；竖直方向是虚轴，每个单位根处也都有明显可辨的空洞。
