你的数学直觉怎么样？你能凭借直觉，迅速地判断出谁的概率大，谁的概率小吗？下面就是 26 个这样的问题。如果你感兴趣的话，你可以先扫一遍所有的问题，再逐一阅读答案，看看你猜对了多少。这篇文章很长，你可以考虑把它加入书签，每天看几个问题。

 

1．A 、 B 、 C 、 D 四人玩扑克牌游戏， A 、 C 两人同盟， B 、 D 两人同盟。将除去大小王的 52 张牌随机分发给四人（每人获得 13 张牌）后，下面哪种情况的可能性更大一些？

A．A 、 C 两人手中都没有梅花
B．A 、 C 两人手中囊括了所有的梅花
C．上述两种情况的出现概率相同

A 、 C 两人手中都没有梅花，等价于 B 、 D 两人手中囊括了所有的梅花，它的概率与 A 、 C 两人手中囊括所有梅花的概率相同。因此，这个问题的答案显然是 C 。

 

2．我给 10 个好朋友分别写了一封信，并把这 10 个人的地址分别写在了 10 个信封上。如果我随机地将这 10 封信装进 10 个信封里（每封信都装进了一个不同的信封里），下面哪种情况的可能性更大一些？

A．恰好有 9 封信装进了正确的信封
B．所有 10 封信都装进了正确的信封
C．上述两种情况的出现概率相同

你或许会以为，全都装对的可能性很低，装错一个的可能性则略高一些。然而事实上，这道题的答案是 B 。原因非常简单：恰好有 9 封信装对，这是根本不可能的——如果其中 9 封信都装对了，剩下的那一封信肯定也装对了。

实际上， 10 封信的排列方式一共有 10! = 3628800 种，其中装对的信有 0, 1, 2, 3, …, 9, 10 封的情况数分别为 1334961, 1334960, 667485, 222480, 55650, 11088, 1890, 240, 45, 0, 1 。可以看到，绝大多数时候，这个数列里的数都是不断递减的；也就是说，装对的信越多，概率就越低，这个直觉确实是准确的。唯一的例外，就是这个数列的最后两项，其背后的原因正如刚才所说。

你或许发现了一个有趣的现象：数列的第二项正好比第一项小 1 。这并不是巧合。有一个普遍的规律是，假设把 n 封信装进 n 个信封里，那么当 n 为偶数时，装对 1 封信的情况数比全都装错的情况数少 1 ，当 n 为奇数时，装对 1 封信的情况数比全都装错的情况数多 1 。我们下面就来证明这一点。

假设把 n 封信装进 n 个信封里，全都装错的情况有 D_n 种。那么，数列 D₁, D₂, D₃, … 满足一个非常简单的递推关系： D_n = (n – 1) (D_n-1 + D_n-2) 。为什么呢？我们慢慢来分析。由于每封信都装错了，因此第 1 封信没有装进 1 号信封。无妨假设它装进了 2 号信封。那么，第 2 封信装到哪儿去了呢？如果第 2 封信正好装进了 1 号信封，那么剩下的 n – 2 封信就有 D_n-2 种可能的装法。如果第 2 封信没有装进 1 号信封呢？情况就变成了这样：第 2, 3, 4, …, n 封信装进了编号分别为 1, 3, 4, …, n 的信封里，其中第 2 封信不在 1 号信封里，第 3 封信不在 3 号信封里，第 4 封信不在 4 号信封里……总之，这 n – 1 封信中，每封信都正好有一个禁放的信封。于是，这就构成了 D_n-1 种可能的装法。当然，第 1 封信也有可能装进了 3 号信封里，也有可能装进了 4 号信封里……因此，我们就有 D_n = (n – 1) (D_n-1 + D_n-2) 。

在这个式子的左右两边同时减去 n · D_n-1 ，于是得到：

D_n – n · D_n-1 = – (D_n-1 – (n – 1) · D_n-2)

令 A_n = D_n – n · D_n-1 ，于是 A_n 满足递推关系式：

A_n = – A_n-1

可以验证：

A₂ = D₂ – 2 · D₁ = 1 – 0 = 1

于是有：

A_n = (-1)ⁿ

即 D_n – n · D_n-1 = (-1)ⁿ 。而 n · D_n-1 正好表示把 n 封信装进 n 个信封里恰好装对 1 封信的情况数。

 

3．桌子上有 A 、 B 两个不透明的盒子，盒子 A 里有 m 个白色小球和 1 个黑色小球，盒子 B 里有 n 个白色小球和 1 个黑色小球。你需要先从盒子 A 里随机取出一个小球，再从盒子 B 里随机取出一个小球。如果两个小球都是黑色的，那么你就获胜了。下面哪种情况下，你获胜的概率更大一些？

A．m = 5，n = 5
B．m = 4，n = 6
C．上述两种情况的获胜概率相同

你或许会以为，反正都是 10 个白色小球，怎么放应该没关系吧。而事实上，在 A 、 B 两种情况下，获胜的概率还真的不一样。在情况 A 中，你获胜的概率为 (1/6) × (1/6) = 1/36 ；在情况 B 中，你获胜的概率为 (1/5) × (1/7) = 1/35 。因此，这个题目的答案是 B 。

如果我们把规则改为，先随机选择其中一个盒子，再从这个盒子中随机取出一个小球，取到黑色小球即获胜，那么情况 B 的获胜概率仍然会更大一些。在情况 A 中，你获胜的概率为 (1/2) × (1/6) + (1/2) × (1/6) = 1/6 ；在情况 B 中，你获胜的概率为 (1/2) × (1/5) + (1/2) × (1/7) = 6/35 。

如果你可以自己安排每个小球的位置（但黑白小球的总数不变），那么不管是在原游戏中还是在改版后的游戏中，为了让自己的胜率达到最大，你都应该在其中一个盒子里只放 1 个黑球，在另一个盒子里放入剩下的 1 个黑球和 10 个白球。这样的话，在原游戏中，你获胜的概率将达到 1 × (1/11) = 1/11 ；在改版后的游戏中，你获胜的概率将达到 (1/2) × 1 + (1/2) × (1/11) = 6/11 。

 

4．不透明的盒子里有 10 个白球和 1 个黑球，你的目标是从中取出黑球。每次，你可以从中随机取出一个小球，并观察它的颜色：如果是黑球，则达到目标，结束操作；如果是白球，则将小球放回盒子里，然后继续像这样随机取球，直到取出了黑球为止。下面哪种情况的可能性更大一些？

A．第 1 次就取到了黑球
B．到第 4 次才取到黑球
C．上述两种情况的出现概率相同

这个题目的答案显然应该是 A 。若每次取出黑球的概率为 p ，则第 1 次就取到黑球的概率为 p ，到第 4 次才取到黑球的概率为 (1 – p) · (1 – p) · (1 – p) · p ，后者永远比前者更低。如果我们把第 n 次才取到黑球的概率记为 P_n ，那么就有：

P_n = (1 – p)^n-1 · p

然而，把 P₁, P₂, P₃, … 全部累加起来的结果应该为 1 ，于是我们用概率论的方法得到公式：

(1 + (1 – p) + (1 – p)² + (1 – p)³ + …) · p = 1

即：

1 + (1 – p) + (1 – p)² + (1 – p)³ + … = 1 / p

令 x = 1 – p ，得到：

1 + x + x² + x³ + … = 1 / (1 – x)

这正是无穷等比级数的求和公式。由于实数 p 必须在 0 到 1 之间，而 x = 1 – p ，因此上式中的 x 也必须在 0 到 1 之间。

 

5．不透明的盒子里有 10 个白球和 1 个黑球。 A 、 B 两人轮流从盒子里取球，每个人每次只能随机从中取出一个小球（取出的小球不再放回）。谁先取到那个黑球，谁就获得游戏的胜利。如果 A 先取，那么理论上，下面哪种情况的可能性更大一些？

A．A 获得游戏的胜利
B．B 获得游戏的胜利
C．上述两种情况的出现概率相同

这个题目的答案是 A 。不妨规定，即使有人取到了黑球，两人也继续往下取，直到把所有的小球都取光。整个游戏就可以等价地看作是，两人轮流取完所有的小球后，看看谁手中有那个黑球。由于 A 先取，因此最后 A 会取到 6 个小球， B 只能取到 5 个小球。所以，黑球在 A 手中的概率更大，等于 6/11 。

类似地，如果不透明的盒子里有 W 个白球和 B 个黑球，不断从里面取出小球（不再放回），那么不管 i 是多少（0 < i ≤ W + B），第 i 次取到的是白球的概率都是 W / (W + B) ，第 i 次取到的是黑球的概率都是 B / (W + B) 。因为，这本质上相当于把所有的小球随机地排成一排，问第 i 个小球是白色或者黑色的概率。

 

6．不透明的盒子里有 2 个白球和 5 个黑球。地上还有足够多的白球和黑球。每次从盒子里随机取出两个小球，放在地上。如果刚才取出的两个小球都是白球，则从地上拿一个白球放入盒子；如果刚才取出的两个小球都是黑球，则从地上拿一个白球放入盒子；如果刚才取出的两个小球是一黑一白，则从地上拿一个黑球放入盒子。不断重复，直至盒子里只剩一个小球为止。那么，下面哪种情况的可能性更大一些？

A．剩下的那个小球是白球

B．剩下的那个小球是黑球
C．上述两种情况的出现概率相同

这是一个很赖皮的题目。它的答案是 B 。事实上，出现情况 A 的概率为 0 ，出现情况 B 的概率为 100% 。原因很简单。每次操作后，黑球的数量要么不变，要么减 2 ，所以黑球的奇偶性始终保持相同。初始时盒子里有奇数个黑球，今后盒子里就永远有奇数个黑球。所以，如果最后盒子里剩了 1 个小球，那它必然是黑球。

 

7．在一根木棒上随机选择两个点，并在这两个点处下刀，把木棒砍成三段。下面哪种情况的可能性更大一些？

A．这三段木棒能拼成一个三角形
B．这三段木棒不能拼成一个三角形
C．上述两种情况的出现概率相同

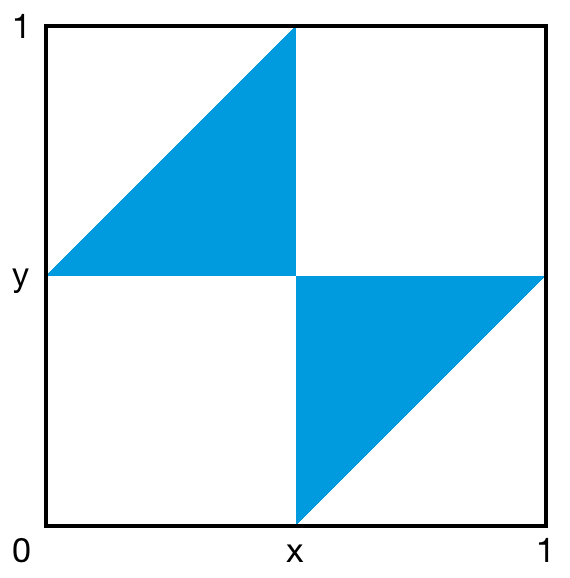
这个题目选 B 。我们可以证明，这三段木棒能拼成三角形的概率是 1/4 。不妨把这根木棒的长度设为 1 ，两个分割点的位置分别记作 x 、 y ，则 x 和 y 都是 0 到 1 之间的随机数。那么，所有可能的 (x, y) 组合就对应了正方形 (0, 1) × (0, 1) 内的所有点。三段木棒能拼成三角形，当且仅当 (x, y) 落在了阴影部分。由于阴影部分占了总面积的 1/4 ，因此这三段木棒能拼成三角形的概率就是 1/4 。

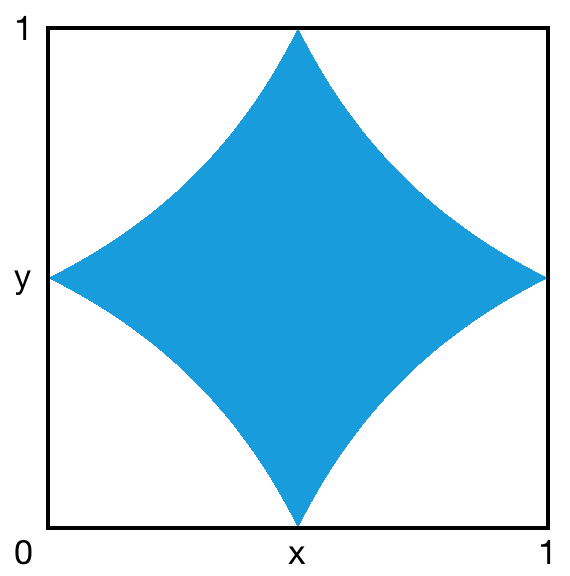
这个题目还有很多变种。比如，如果先把木棒随机砍成两段，再把较长的那段木棒随机砍成两段，问这三段木棒能拼成一个三角形的概率是多少。这该怎么解呢？你或许会说，为何不像刚才那样，把第一个分割点和第二个分割点的位置分别记作 x 、 y ，然后套用刚才的面积大法？这次就不行了，因为 y 的值不再能独立而均匀地分布在 0 到 1 之间。但是，我们可以令 x 为第一个分割点在整根木棒上的比例，令 y 为第二个分割点在较长的那段木棒上的比例。举个例子， (x, y) = (1/3, 1/3) 的意思就是，先把整根木棒砍成 1 : 2 两段，再把较长的那段木棒砍成 1 : 2 两段。这样一来，所有可能的 (x, y) 组合就再一次均匀地对应了正方形 (0, 1) × (0, 1) 内的所有点。最终，三段木棒能拼成三角形，当且仅当 (x, y) 落在由 x · y < 1/2, (1 – x) · y < 1/2, x · (1 – y) < 1/2, (1 – x) · (1 – y) < 1/2 组成的交集区域里。利用定积分可以求出，这部分区域的面积占整个正方形面积的 2 · ln(2) – 1 ≈ 38.63% 。这就是答案。

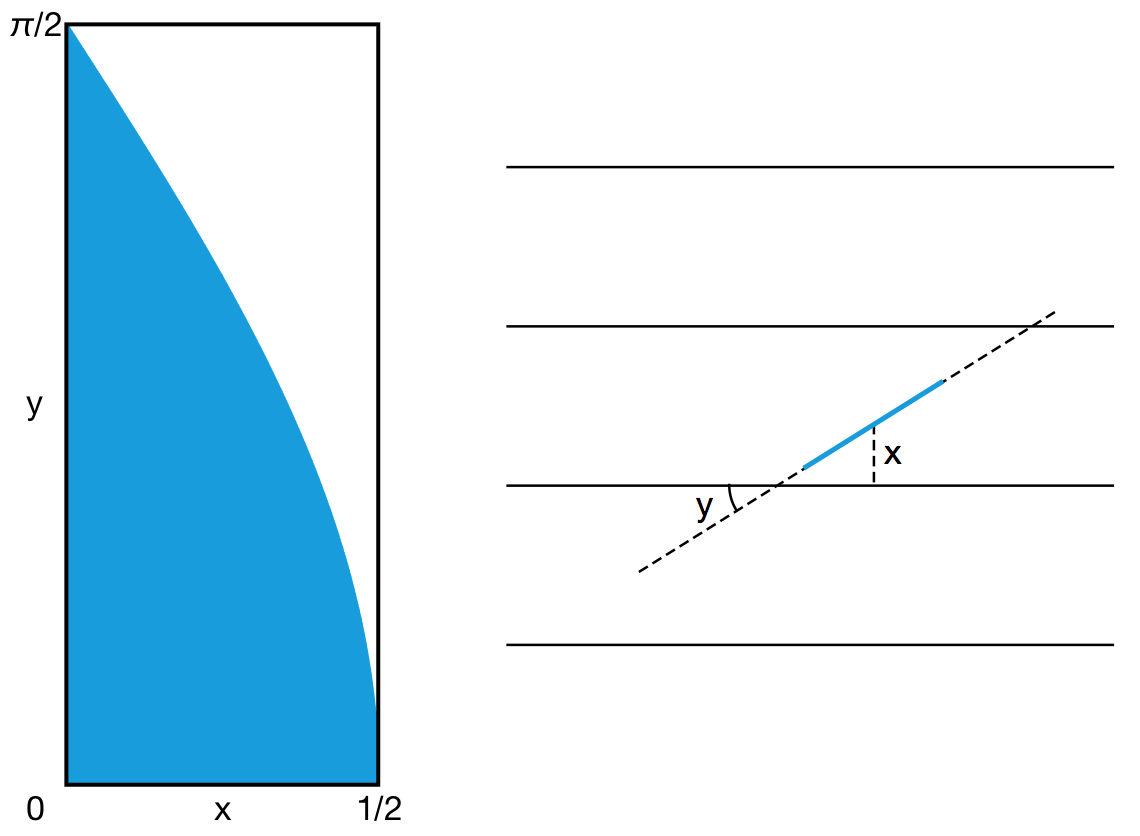
著名的 Buffon 投针问题，标准解法之一也用到了这种模型。在地板上画一系列间隔为 1 厘米的平行直线，然后把一根 1 厘米长的针扔到地板上，它与直线有交点的概率是多少？令 x 为这根针的中心到离它最近的那条直线的距离，令 y 为这根针与平行线的夹角。所有可能的针的位置，就可以用所有可能的 (x, y) 组合来表示，它们正好对应了矩形 (0, 1/2) × (0, π/2) 内的所有点。其中，合法的区域为 y < arccos(2x) ，它占矩形面积的 2 / π ≈ 63.66% 。这就是答案。

高中数学课本把这种解决概率问题的模型叫做“几何概型”。说到几何概型，最经典的可能要算下面这个例题。 A 、 B 两人约定好晚上 6:00 到 7:00 之间在公园门口见面。每个人都会从 6:00 到 7:00 这段时间当中随机挑选一个时间，并在这个时间到达公园门口。每个人都只愿意等待 15 分钟，也就是说，如果 15 分钟之后没有看见对方，那么就立即离开。那么，两人最终能见面的概率有多大？答案是 7/16 。

 

8．圆周上均匀分布着 100 个点。随便选择两个点连一条线段，再随便选择另外两个点连一条线段。那么，下面哪种情况的可能性更大一些？

A．两条线段相交
B．两条线段不相交
C．上述两种情况的出现概率相同

这个题目的答案是 B 。随便选择两个点，再随便选择另外两个点，本质上相当于先随便选择四个点，再决定把这四个点配成怎样的两对。对于任意四个点 A 、 B 、 C 、 D （在圆周上按此顺序排列）来说，我们都有三种不同的配对方案：① A – B, C – D ② A – C, B – D ③ A – D, B – C 。其中，只有方案 ② 对应的两条连线才会相交。因此，两条线段相交的概率是 1/3 。

 

9．不透明的盒子里有 1000 张纸条，上面分别写有 1, 2, 3, …, 1000。 A 从盒子里随机取出 100 张纸条，并把这 100 张纸条上的数从小到大排成一排。然后， B 从盒子里剩下的纸条中随机取出 1 张纸条，并看看这张纸条上的数在 A 那里排第几位。例如，如果 A 手中的数有 50 个比 B 取出的大，另外 50 个比 B 取出的小，那么 B 手中的数就排第 51 位。那么，下面哪种情况的可能性更大一些？

A．B 手中的数排第 1 位
B．B 手中的数排第 51 位
C．上述两种情况的出现概率相同

很多人的直觉都是，排第 1 可能性不大，排中间可能性更大。而实际上，考虑所有 101 个数的 101! 种排列方案，或者从 1000 个数里选 101 个数所产生的 P(1000, 101) 种排列方案， B 选的那个数将会等可能地出现在各个位置。因此，这个题目的答案是 C 。

如果你还想不明白的话，你干脆直接想成是， A 抽了 100 个数，然后再帮 B 抽了一个数，问帮 B 抽的这个数更有可能排第几。如果你还想不明白的话，你干脆直接想成是， A 抽了 101 个数，问最后抽出的这个数更有可能排第几。如果你还想不明白的话，你干脆直接想成是， A 选了 101 个数往空中一撒，问最后一个落地的数更有可能是排第几的数。

 

10．把一副洗好的牌（共 52 张）背面朝上地摞成一摞，然后依次翻开每一张牌，直到翻出第一张 A 。那么，下面哪种情况的可能性更大一些？

A．翻开第 3 张牌时出现了第一张 A
B．翻开第 4 张牌时出现了第一张 A
C．上述两种情况的出现概率相同

这个题目的答案是 A 。这个答案并不出人意料。你不妨考虑一个非常极端的情况：假设一副牌里只有三张牌，其中两张是 A ，另外一张是 2 。那么，洗好牌后，三张牌的顺序有 AA2, A2A, 2AA 三种（如果把两张 A 看作是两张不同的 A ，那么三张牌的顺序有 A₁A₂2, A₂A₁2, A₁2A₂, A₂2A₁, 2A₁A₂, 2A₂A₁ 六种）。翻到第 1, 2, 3 张牌时出现第一张 A 的概率分别是 2/3, 1/3, 0 。

至于原题为什么选 A ，我们给出一个这样的解释。洗好牌后，从前往后四张 A 所在的位置一共有 C(52, 4) 种可能的情况，分别为 (1, 2, 3, 4), (1, 2, 3, 5), (1, 2, 3, 6), …, (49, 50, 51, 52) 。其中，形如 (3, ?, ?, ?) 的情况显然比形如 (4, ?, ?, ?) 的情况更多，因为前者的问号处可以有更丰富的取值。

 

11．把一副洗好的牌（共 52 张）背面朝上地摞成一摞，然后依次翻开每一张牌，直到翻出第一张 A 。那么，下面哪种情况的可能性更大一些？

A．再下一张牌是黑桃 A
B．再下一张牌是黑桃 2
C．上述两种情况的出现概率相同

很多人可能会认为，下一张牌是黑桃 2 的可能性更大，因为刚才翻出的首张 A 可能就是黑桃 A 。其实这种直觉是错误的。令人吃惊的是，这道题的答案是 C 。下一张牌是黑桃 A 的概率与下一张牌是黑桃 2 的概率一样大，它们都等于 1/52 。

为了说明这一点，我们不妨来看一种同样能实现绝对随机的另类洗牌方式：先把一副牌中的黑桃 A 抽出来，随机洗牌打乱剩下 51 张牌的顺序，然后把黑桃 A 插回这摞牌中（包括最顶端和最底端在内，共有 52 个可以插入的位置）。显然，黑桃 A 正好插到了这摞牌的首张 A 下面有 1/52 的可能性。根据同样的道理，首张 A 下面是黑桃 2 的概率也是 1/52 。事实上，任何一张牌都有可能出现在首张 A 的下面，它们出现的概率是相等的，都等于 1/52 。

 

12．把一副洗好的牌（共 52 张）背面朝上地摞成一摞。翻开最上面的那张牌，记住这张牌是什么颜色（红色还是黑色），然后将它背面朝上地放回原处。随机切一次牌（即把扑克牌随机分成上下两摞，把下面这摞牌叠在上面这摞牌的上面），然后再次翻开最上面的那张牌，记住这张牌是什么颜色（红色还是黑色）。那么，下面哪种情况的可能性更大一些？

A．两次看到的牌的颜色相同
B．两次看到的牌的颜色不同
C．上述两种情况的出现概率相同

答案很简单：选 B 。这是因为，切了一次牌之后，你刚才翻开的那张牌就不可能在最上面了。换句话说，再次翻开的牌将会等可能地是剩余的 51 张牌中的任何一张，其中有 26 张牌和你第一次翻开的牌颜色不同，但只有 25 张牌和你第一次翻开的牌颜色相同。

 

13．同时抛掷 10 枚硬币，出现下面哪种情况的可能性更大一些？

A．正面朝上的硬币数量为偶数
B．正面朝上的硬币数量为奇数
C．上述两种情况的出现概率相同

答案是 C 。事实上，把 10 换成任意正整数，这个问题的答案都不会变——正面朝上的硬币个数是奇是偶的概率一样大。

让我们把这个问题先修改一下：同时抛掷 5 枚硬币，正面朝上的硬币数量为偶数的概率大，还是为奇数的概率大？有趣的是，新的问题突然有了一种非常简单的解法。我们可以把同时抛掷 5 枚硬币的结果分成六大类： 0 个正面 5 个反面、 1 个正面 4 个反面、 2 个正面 3 个反面、 3 个正面 2 个反面、 4 个正面 1 个反面、 5 个正面 0 个反面。我们把这六类情况分成三组：

• 0 正 5 反， 5 正 0 反
• 2 正 3 反， 3 正 2 反
• 4 正 1 反， 1 正 4 反

注意到，每一组里的前后两类情况出现的概率总是相同的，然而前面那类总是属于有偶数个正面的情况，后面那类总是属于有奇数个正面的情况。因而总的来说，有偶数个正面的情况和有奇数个正面的情况将会概率均等地出现。

回到原问题。如果是 10 枚硬币的话，又该怎么办呢？大家或许想要故技重施，但却发现这回不管用了。虽然 0 正 10 反和 10 正 0 反出现的概率仍然相等，但它们都是有偶数个正面的情况，这样就没法推出奇偶两种情况各占一半的结论了。不过，我们另有奇招。把这 10 枚硬币分成两组，每一组各有 5 枚硬币。根据刚才的结论，每组硬币里面出现偶数个正面和出现奇数个正面的概率是相同的，因而，同时抛掷这两组硬币后，检查两组硬币正面朝上的数量分别有多少，会产生“偶偶”、“偶奇”、“奇偶”、“奇奇”这四种等概率的组合。在第一种情况和最后一种情况中，最终正面朝上的硬币数量为偶数；在第二种情况和第三种情况中，最终正面朝上的硬币数量为奇数。可以看到，正面朝上的硬币数量是奇是偶的概率相等。

我们还有另一种更简单的方法来说明，同时抛掷 10 枚硬币后，正面朝上的硬币数量是奇是偶的概率的确相同。假设你已经抛掷了 9 枚硬币，正准备抛掷最后一枚硬币。不管前 9 枚硬币抛掷成啥样，最后这枚硬币的正反都将会起到决定性的作用，具体情况分为两种，视前 9 枚硬币的抛掷结果而定：

• 如果最后一枚硬币是正面，总的正面个数就是偶数；如果最后一枚硬币是反面，总的正面个数就是奇数；
• 如果最后一枚硬币是正面，总的正面个数就是奇数；如果最后一枚硬币是反面，总的正面个数就是偶数。

容易看出，不管是上述两种情况中的哪种情况，总的正面个数是奇是偶的概率都是相等的。因此，即使上述两种情况出现的概率不相等（当然，事实上是相等的），最终总的正面个数是奇是偶的概率也是相等的。

 

14．A 、 B 两人在玩掷硬币游戏，每个人都抛掷 10 次硬币，最后谁抛出的正面更多，谁就获胜。几轮游戏下来后， A 都获胜了， B 有些沮丧。 A 说：“要不这样吧，我们把游戏规则改一下。我允许你多抛掷一次硬币。也就是说，我仍然抛掷 10 次硬币，你却能抛掷 11 次硬币。但是，只有你抛掷出的正面次数严格大于我抛掷出的正面次数，才算你获胜；如果我们抛掷出的正面次数相同，那也算我获胜。”新的一轮游戏开始了，按照约定， A 抛掷了 10 次硬币， B 抛掷了 11 次硬币。理论上，下面哪种情况的可能性更大一些？

A．A 获得游戏的胜利
B．B 获得游戏的胜利
C．上述两种情况的出现概率相同

题目的答案是 C 。这是一个非常经典的问题，解决它的方法也有很多。我们介绍两种方法。

第一种方法如下。在新版游戏中，假设两人各自都已经抛掷了 10 次硬币，只待 B 抛掷最后一次了。此时，如果 B 的正面更多，那他就胜定了，游戏可以提前结束了。如果 B 的正面更少，那他就输定了，游戏也可以提前结束了。显然，这两种情况出现的概率相同。现在，只剩一种情况有待分析，即此时 B 的正面数量与 A 相同。那么，游戏结果将完全取决于 B 的最后一次抛掷：如果 B 抛掷出正面，胜；如果 B 抛掷出反面，败。而这两种情况出现的概率也是相同的。综上所述，新的游戏是公平的。

第二种方法如下。既然 B 比 A 多抛掷一次，那这就说明， B 的正面和反面不可能都没 A 多（否则 B 的硬币总数不可能比 A 多）。另外，由于 B 只比 A 多抛掷一次，那这就说明， B 的正面和反面不可能都比 A 多（否则 B 的硬币总数至少比 A 大 2 ）。综上所述，要么 B 的正面比 A 更多，要么 B 的反面比 A 更多。由于硬币本身是公正的，因此这两种情况出现的几率相等，它们各为 1/2 。但是， B 的正面比 A 更多就意味着 B 获胜了， B 的反面比 A 更多就意味着 B 的正面数量不比 A 多，即 A 获胜了（别忘了，平局算 A 获胜）。所以，两人各自获胜的概率都是 1/2 。

 

15．魔术师把一枚正常的硬币展示给观众看，然后说：“接下来，我会抛掷这枚硬币，每次它都将正面朝上。”观众听闻后议论纷纷，魔术师趁机迅速地把这枚正常的硬币换成了一枚两面都是正面的硬币。魔术师连掷 10 次硬币，次次正面朝上，赢得观众雷鸣般的掌声。其中一个观众不服气地说：“该不会你趁我们不注意，把硬币换成了两面都是正面的特殊硬币吧！如果你有本事的话，你给我们掷出一个‘正反正反……’的序列出来！”为了保住自己的颜面，魔术师只好把那枚正常的硬币变回手中，硬着头皮开始抛掷硬币。倘若魔术师抛掷硬币没有任何技巧，每次是正是反的概率相同，那么魔术师无限地抛掷下去，第一次出错更有可能出在什么地方？

A．该掷正面的时候掷出了反面
B．该掷反面的时候掷出了正面
C．上述两种情况的出现概率相同

这个题目的答案是 A 。下面我们证明，因为该掷反面的时候掷出了正面而挂掉的概率，也就是在第偶数次抛掷时挂掉的概率，精确地等于 1/3 。容易得出，第 2 次就挂了的概率就是前 2 次精确地掷出“正正”序列的概率，它等于 1 / 2² 。类似地，到第 4 次才挂的概率就是前 4 次精确地掷出“正反正正”序列的概率，它等于 1 / 2⁴ ；而到第 6 次才挂的概率则是前 6 次精确地掷出“正反正反正正”序列的概率，它等于 1 / 2⁶……所以，在第偶数次挂掉的概率是：

  1 / 2² + 1 / 2⁴ + 1 / 2⁶ + 1 / 2⁸ + …
= 1 / 4 + 1 / 4² + 1 / 4³ + 1 / 4⁴ + …
= (1 + 1 / 4 + 1 / 4² + 1 / 4³ + 1 / 4⁴ + …) – 1
= 1 / (1 – 1 / 4) – 1
= 1 / 3

倒数第二步用到了无穷等比级数的求和公式（见本文中的第 4 题）。

其实，这个答案有一个非常直观的解释。想象 A 、 B 两人玩一个掷硬币游戏。两人轮流抛掷硬币，但 A 必须掷出正面， B 必须掷出反面，谁掷错了谁就立即输掉游戏。如果 A 先抛硬币，谁输掉的概率更大？那当然是 A 输掉的概率更大，因为他先掷嘛！

事实上，设 A 输掉的概率为 p ，我们可以巧妙地求出 p 来。怎样的情况下 A 才会输掉呢？如果 A 第一次就掷错了，他就直接输了，这有 1/2 的概率。如果 A 第一次掷对了，那么 B 必须也跟着掷对，走到这一步有 (1/2) × (1/2) = 1/4 的概率。此时，游戏又回到了出发点， A 输掉的概率又变回了 p 。于是，我们得到：

p = 1/2 + (1/4) · p

把它当作一个关于 p 的一元一次方程，解得 p = 2/3 。这就是我们想要的答案。我们将会在很后面的几个题目里继续用到这种技巧。

我们还有一种非常帅的方法来说明，为什么魔术师首次出错更容易错在把正面掷成了反面。把正面看作数字 1 ，反面看作数字 0 ，那么观众要求的目标序列就变成了 101010… 。如果在前面加一个小数点，这就变成了一个 0 到 1 之间的二进制小数 0.101010… ，它等于十进制中的 2/3 。而魔术师抛掷的硬币序列，则构成了一个 0 到 1 之间的随机数。如果某一次把 0 掷成了 1 ，就说明掷出的是一个比 2/3 更大的数；如果某一次把 1 掷成了 0 ，就说明掷出的是一个比 2/3 更小的数。显然，前者的概率是 1/3 ，后者的概率是 2/3 。

你意识到了吗？我们相当于用一枚公正的硬币，模拟出了一枚不公正的硬币。如果你想要一枚硬币，它有 2/3 的概率正面朝上，有 1/3 的概率反面朝上，但你手中只有一枚公正的硬币，你该怎么办呢？你可以像刚才那样，不断抛掷硬币，得出一个 0 到 1 之间的随机二进制小数。一旦发现这个二进制小数小于 2/3 ，就视最终结果为“正”；一旦发现这个二进制小数大于 2/3 ，就视最终结果为“反”。

当然，模拟这样一枚不公正的硬币，其实远不需要这么麻烦。我们可以连续抛掷 2 次硬币，抛出“正反”或者“反正”都视最终结果为“正”，抛出“正正”则视最终结果为“反”，抛出“反反”则此轮抛掷作废，重头再来。这种“分类讨论法”能成的原因是， 2/3 是一个有理数。如果我们要模拟一枚不公正的硬币，它有 1 / π 的概率正面朝上，有 1 – 1 / π 的概率反面朝上呢？此时，“分类讨论法”就不管用了。但是，刚才的“二进制小数法”依旧有效。不断抛掷硬币并记录抛掷结果， 1 代表正面， 0 代表反面，直至某次掷出的结果与 1 / π 的二进制小数不符。如果是 1 被掷成 0 了，则视最终结果为“正”；如果是 0 被掷成 1 了，则视最终结果为“反”。

如何用一种硬币去模拟另一种硬币，这是一个非常有趣的话题，里面大有文章可作。比方说，我们完全可以提出一个和刚才的问题正好相反的问题：如果你手里有一枚不公正的硬币（你不知道它的正反两面朝上的概率各是多少，你甚至不知道它的哪一面朝上的概率更大），如何才能把它当作一枚公正的硬币来使？办法有很多。比方说，考虑连续抛掷两次硬币后的结果：如果结果是一正一反，那么先正后反和先反后正的概率一定是相同的（即使这枚硬币是不公平的）。借助这一点，我们就有了下面这个方案：连续抛掷两次硬币，如果两次抛掷的结果是“正反”，就视最终结果为“正”；如果两次抛掷的结果是“反正”，就视最终结果为“反”；如果是其他情况，就重新再来。

如果把两种甚至更多种不同的硬币组合起来使用，在某些限制条件下模拟出某些特定的概率事件，这里面的水就更深了。这里有一个与此相关的问题，感兴趣的话不妨去看看： http://www.matrix67.com/blog/archives/6151 。

 

16． A 、 B 两人为一件小事争执不休，最后决定用抛掷硬币的办法来判断谁对谁错。不过，为了让游戏过程更刺激，两人决定采用这样一种方案：连续抛掷硬币，直到最近三次硬币抛掷结果是“正反反”或者“反反正”。如果是前者，那么 A 获胜；如果是后者，那么 B 获胜。理论上，下面哪种情况的可能性更大一些？

A．A 获得游戏的胜利
B．B 获得游戏的胜利
C．上述两种情况的出现概率相同

乍看上去， B 似乎没有什么不同意这种玩法的理由，毕竟“正反反”和“反反正”的概率是均等的。连续抛掷三次硬币可以产生 8 种不同的结果，上述两种各占其中的 1/8 。况且，序列“正反反”和“反反正”看上去又是如此对称，获胜概率怎么看怎么一样。

不过，实际情况究竟如何呢？实际情况是，这个游戏并不是公平的—— A 的获胜概率是 B 的 3 倍！虽然“正反反”和“反反正”在一串随机硬币正反序列中出现的频率理论上是相同的，但别忘了这两个序列之间有一个竞争的关系，它们要比赛看谁先出现。一旦抛掷硬币产生出了其中一种序列，游戏即宣告结束。这样一来， B 就处于了一个非常窘迫的位置：不管什么时候，只要掷出了一个正面，如果 B 没赢的话， B 就赢不了了——在出现“反反正”之前， A 的“正反反”必然会先出现。

事实上，整个游戏的前两次硬币抛掷结果就已经决定了两人最终的命运。只要前两次抛掷结果是“正正”、“正反”、“反正”中的一个， A 都必胜无疑， B 完全没有翻身的机会；只有前两次掷出的是“反反”的结果， B 才会赢得游戏的胜利。因此， A 、 B 两人的获胜概率是三比一， A 的优势绝不止是一点。所以说，这道题目的正确选项为 A 。

这里有对此游戏更加深入的讨论： http://www.matrix67.com/blog/archives/6015 。

似乎是还嫌游戏双方的胜率差异不够惊人， 2010 年， Steve Humble 和 Yutaka Nishiyama 提出了上述游戏的一个加强版。去掉一副扑克牌中的大小王，洗好剩下的 52 张牌后，一张一张翻开。一旦出现连续三张牌，花色依次是红黑黑，那么玩家 A 加一分，同时把翻开了的牌都丢掉，继续一张张翻没翻开的牌；类似地，一旦出现连续三张牌恰好是黑黑红，则玩家 B 得一分，弃掉已翻开的牌后继续。

容易看到，加强版游戏相当于是重复多次的掷硬币游戏，因而毫无疑问，在这个新游戏中，玩家 A 的优势还会进一步放大。电脑计算显示， A 获胜的概率高达 93.54% ， B 获胜的概率则只有可怜的 2.62% 。另外 3.84% 则是两人平手的概率。然而，即使是这样，这个游戏看上去也会给人一种公平的错觉！

这个例子告诉我们，在赌博游戏中，直觉并不是准确的，求助概率论是很有必要的。

其实，概率论的诞生本来就和赌博游戏是紧紧联系在一起的。提到概率论的诞生，不得不提一位名叫 Antoine Gombaud 的法国作家。这人出生于 1607 年法国西部的一个小城市，他并不是贵族出身，但他却有着“骑士”的光辉头衔——不过那只是他自封的而已。他借用了一个自己笔下的人物形象名称，自封为 de Méré 骑士。后来，这个名字便逐渐取代了他的真名 Antoine Gombaud 。不过， de Méré 骑士并没有凭借自己的文学作品名扬天下，真正让他声名远扬的是他的赌博才能。而足以让他在历史上留名的，则是他对一个赌博游戏的思考。

在 17 世纪，法国赌徒间流行着一个赌博游戏：连续抛掷一颗骰子 4 次，赌里面是否会出现至少一个 6 点。这个游戏一直被视为是一个公平的赌博游戏，直到 1650 年左右， de Méré 在另一个类似的游戏中莫名其妙地输得四个荷包一样重。当时， de Méré 参加了这个赌博游戏的一个“升级版”：把两颗骰子连续抛掷 24 次，赌是否会掷出一对 6 点来。

de Méré 自己做了一番思考。同时抛掷两颗骰子出现一对 6 ，比抛掷一颗骰子出现 6 点要困难得多，前者的概率是后者的 1/6 。要想弥补这个减小了的概率，我们应当把两颗骰子连续抛掷 6 次。为了追上连续抛掷 4 次骰子出现一个 6 的概率，则应当把两颗骰子抛掷 24 次才行。 de Méré 果断地得出结论：在升级版游戏中出现一对 6 的概率，与传统游戏中出现一个 6 的概率是相等的，升级版游戏换汤不换药，与原来的游戏本质完全一样。

不过，这毕竟是不严格的直觉思维，事实情况如何还得看实战。在以前的游戏中， de Méré 总是赌“会出现 6 点”，经验告诉他这能给他带来一些细微的优势。于是这一回， de Méré 也不断押“会出现一对 6”。不料，这次他却赔得多赚得少，最终输了个精光。

这是怎么一回事儿呢？作为一个业余数学家， de Méré 感到里面有玄机。但是，凭借自己的数学知识，他没有能力解决这个难题。无奈之下，他只好求助当时的大数学家 Blaise Pascal 。

Pascal 可是真资格的数学家。他很快便意识到，这种问题的计算不能想当然，事实和直觉的出入可能会相当大。比方说， de Méré 的直觉就是有问题的：重复多次尝试确实能增大概率，但这并不是成倍地增加。抛掷一颗骰子出现 6 点的概率为 1/6 ，但这并不意味着抛掷骰子 4 次会出现一个 6 点的概率就是 1/6 的 4 倍。无妨想一个更极端的例子：按此逻辑，抛掷一颗骰子 6 次，出现至少一次 6 点的概率似乎就该是 6/6 ，也即 100% ，但这显然是不对的。如果抛掷骰子 6 次以上，出现一个 6 点的概率就会超过 100% ，这就更荒谬了。

看来，概率不能简单地加加减减，每一步推理都要有凭有据。 Pascal 考虑了游戏中所有可能出现的情况，算出了在新旧两种版本的游戏中，会出现一个（或一对） 6 点的概率分别是多少。

连续抛掷 4 次骰子，总共会产生 6⁴ ，也就是 1296 种可能。不过在这里面，一个 6 点都没有的情况共有 5⁴ ，也就是 625 种。反过来，至少有一个 6 点就有 1296 – 625 = 671 种情况，它占所有情况的 671 / 1296 ≈ 51.77% ，恰好比 50% 高出那么一点点。看来， de Méré 的经验是对的——众人公认的公平游戏并不公平，赌 6 点会出现确实能让他有机可乘。

那么，连续抛掷两颗骰子 24 次，能出现一对 6 的概率又是多少呢？这回计算的工程量就有点大了。两颗骰子的点数有 36 种组合，连抛 24 次则会有 36²⁴ ，大约是 2.245 × 10³⁷ 种情况。而 24 次抛掷中，从没产生过一对 6 点的情况数则为 35²⁴ ，大约为 1.142 × 10³⁷ 。可以算出，如果赌 24 次抛掷里会出现一对 6 ，获胜的概率是 49.14% 。又一个非常接近 50% 的数，只不过这次是比它稍小一些。

原来，升级版游戏并不是换汤不换药。两种游戏胜率虽然接近，但正好分居 50% 两边。这看似微不足道的差别，竟害得我们的“骑士”马失前蹄。

后来，这个经典的概率问题就被命名为“de Méré 问题”。在解决这个问题的过程中， Pascal 提出了不少概率的基本原理。因此， de Méré 问题常被认为是概率论的起源。

当然， de Méré 的故事多少都有一些杜撰的成分，大家或许会开始怀疑，在现今世界里，有没有什么还能玩得到的“伪公平游戏”呢？答案是肯定的。为了吸引玩家，赌场想尽各种花样精心设计了一个个迷魂阵一般的赌局。在那些最流行的赌博游戏中，庄家一方总是会稍占便宜；但游戏规则设计得如此之巧妙，以至于乍看上去整个游戏是完全公平，甚至是对玩家更有利的。“骰子掷好运”（chuck-a-luck）便是一例。

“骰子掷好运”的规则看上去非常诱人。每局游戏开始前，玩家选择 1 到 6 之间的一个数，并下 1 块钱的赌注。然后，庄家同时抛掷三颗骰子。如果这三颗骰子中都没有你选的数，你将输掉那 1 块钱；如果有一颗骰子的点数是你选的数，那么你不但能收回你的赌注，还能反赢 1 块钱；如果你选的数出现了两次，你将反赢 2 块钱；如果三颗骰子的点数都是你选的数，你将反赢 3 块钱。用赌博的行话来说，你所押的数出现了一次、两次或者三次，对应的赔率分别是 1:1 、 1:2 、 1:3 。

用于抛掷三颗骰子的装置很有创意。它是一个沙漏形的小铁笼子，三颗骰子已经预先装进了这个笼子里。庄家“抛掷”骰子，就只需要把整个沙漏来个 180 度大回旋，倒立过来放置即可。因此，“骰子掷好运”还有一个别名——“鸟笼”（birdcage）。

18 世纪英国皇家海军的水手间流行过一种叫做“皇冠和船锚”（Crown and Anchor）的赌博游戏，其规则与“骰子掷好运”一模一样。唯一不同之处只是骰子而已。普通骰子的六个面分别是 1 点到 6 点，而“皇冠和船锚”所用骰子的六个面则是六种不同的图案——扑克牌的黑、红、梅、方，再加上皇冠和船锚两种图案。之后，“赌博风”又蔓延到了商船和渔船上，“皇冠和船锚”也就逐渐走出了皇家海军的圈子。一般认为，这也就是“骰子掷好运”的起源了。现在，很多赌场都提供了“骰子掷好运”的赌博项目。

对玩家而言，这个游戏看上去简直是在白送钱：用三颗骰子掷出 6 个数中的一个，怎么也会有一半的概率砸中吧，那玩家起码有一半的时间是在赚钱，应当是稳赚不赔呀。其实，这是犯了和 de Méré 一样的错误——一颗骰子掷出玩家押的数有 1/6 的概率，并不意味着三颗骰子同时抛掷就会有 3/6 的概率出现此数。在抛掷三颗骰子产生的所有 6³ 种情况中，玩家押的数一次没出现有 5³ 种情况，所占比例大约是 57.87% 。也就是说，大多数时候玩家都是在赔钱的。

不过，考虑到赚钱时玩家有机会成倍地赢钱，这能否把输掉的钱赢回来呢？一些更为细致的计算可以告诉我们，即使考虑到这一点，游戏对玩家仍然是不利的：平均每赌 1 块钱就会让玩家损失大约 8 分钱。不过，我们还有另一种巧妙的方法，无需计算便可看出这个游戏对玩家是不利的。

这显然是一个没有任何技巧的赌博游戏，不管押什么胜率都是一样的。因此，不妨假设有 6 名玩家同时在玩这个游戏，这 6 个人分别赌 6 个不同的点数。此时玩家联盟的输赢也就足以代表单个玩家的输赢了。

假设每个人都只下注 1 块钱。抛掷骰子后，如果三颗骰子的点数都不一样，庄家将会从完全没猜中点数的三个人手中各赚 1 块，但同时也会赔给另外三人各 1 块钱；如果有两颗骰子点数一样，庄家会从没猜中点数的四个人那里赢得共 4 块，但会输给另外两人 3 块；如果三颗骰子的点数全一样，庄家则会赢 5 块但亏 3 块。也就是说，无论抛掷骰子的结果如何，庄家都不会赔钱！虽然一轮游戏下来有的玩家赚了，有的玩家亏了，但从整体来看这 6 名玩家是在赔钱的，因此平均下来每个玩家也是在不断输钱的。

 

17．同时抛掷 6 颗骰子，出现下面哪种情况的可能性更大一些？

A．不同数字的个数恰好为 4 个
B．不同数字的个数为 1 、 2 、 3 、 5 或 6 个
C．上述两种情况的出现概率相同

这个题目的答案竟然是 A ，没想到吧！赌博游戏的胜率常常违反直觉，这道题目又是一个经典的例子。同时抛掷 6 颗骰子，一共会产生 6⁶ = 46656 种情况。其中，不同数字的个数恰好为 4 个的情况有多少种呢？如果 6 颗骰子里只有 4 个不同的数字，那么有的数字出现了至少 2 次。事实上，各个数字出现的次数只有以下两种可能的分布类型：

• 其中 1 个数字出现了 3 次，另外 3 个数字各出现了 1 次
• 其中 2 个数字各出现了 2 次，另外 2 个数字各出现了 1 次。

前者一共有 C(6, 3) × C(6, 4) × 4! = 7200 种具体的情况，其中 C(6, 3) 表示出现了 3 次的数字究竟出现在了哪 3 次， C(6, 4) 表示这 4 个数字究竟是哪 4 个数字。后者一共有 C(6, 2) × C(4, 2) × C(6, 4) × 4! / 2 = 16200 种具体的情况，其中 C(6, 2) 表示第一个出现了 2 次的数字究竟出现在了哪 2 次， C(4, 2) 表示第二个出现了 2 次的数字究竟出现在了哪 2 次， C(6, 4) 表示这 4 个数字究竟是哪 4 个数字，最后的结果除以 2 的原因是，第一个出现了 2 次的数和第二个出现了 2 次的数有可能分别是我和你，也有可能分别是你和我，这被算重了。

因此，不同数字的个数恰好为 4 个的情况一共有 7200 + 16200 = 23400 种，它占总数的 23400 / 46656 ≈ 50.154321% 。

 

18．小明走进一家赌场，来到了轮盘赌跟前。轮盘赌的转盘上有 38 个格子，上面分别标着 0, 00, 1, 2, 3, …, 36 。游戏开始后，一个白色小球会逆着轮盘旋转的方向滚动，最终等概率地落入 38 个格子中的一个。小明每次可以在任意一个格子上下 1 元的赌注。如果小球落入了小明所选的格子里，则小明赢得 36 元（但那 1 元钱的赌注仍然归赌场）；如果小球落入了别的格子里，则小明什么也得不到（那 1 元也就打水漂了）。小明身上只有 105 元钱，于是，他连续赌了 105 次。那么，下面哪种情况的可能性更大一些？

A．小明赚着离开了赌场
B．小明亏着离开了赌场
C．上述两种情况的出现概率相同

花 1 元赌某一个格子，中签的概率是 1/38 ，但却只能赢来 36 元。毫无疑问，轮盘赌是一个赤裸裸的对赌场更有利的赌博游戏。所以，这道题应该选 B 咯？不对！这道题的正确答案其实是 A 。在这道题中， 105 这个数起到了比较关键的作用。让我们来实际计算一下。

由于每赢一次会得到 36 元，因此小明只需要赢 3 次或 3 次以上，便能实现赚着离开赌场了。小明一次没赢的概率为 (37/38)¹⁰⁵ ≈ 0.0608 ，恰好赢 1 次的概率为 C(105, 1) × (1/38) × (37/38)¹⁰⁴ ≈ 0.1725 ，恰好赢 2 次的概率为 C(105, 2) × (1/38)² × (37/38)¹⁰³ ≈ 0.2425 ，上述三个值加起来约为 0.4758 。所以，反过来，小明赢了 3 次或 3 次以上的概率就是 0.5242 ，这超过了 1/2 。

为什么在玩一个明显对赌场更有利的赌博游戏中，精确地花费 105 元钱，就能做到赚时多亏时少？如果每个人都这么做，赌场岂不是会被搞垮？这不跟游戏对赌场更有利的结论相矛盾吗？其实，赚的时候更多，并不意味着期望收益为正。虽然赚的时候多，亏的时候少，但赚的时候往往是赚小钱，亏的时候往往是亏大钱，平均算下来，玩家仍然是在不断送钱的。

 

19．法国有法国的轮盘赌，俄罗斯也有俄罗斯的轮盘赌。不过，战斗民族的赌博方式可不一样——不是赌钱，而是赌命。俄罗斯轮盘赌可谓是史上最酷的决斗方式。左轮手枪的转轮中有六个弹槽。在其中一个弹槽中放入一颗子弹，然后快速旋转转轮，再把它合上。参与决斗的两个人轮流对准自己的头部扣动扳机，直到其中一方死亡。这是一场真男人游戏，双方胜负的概率各占 50% ，游戏没有任何技巧可言，命运决定了一切。为了让游戏更加刺激，这一回我们稍微改变一下游戏规则。在转轮的连续三个弹槽中放入子弹，然后旋转并合上转轮。这一次，理论上，下面哪种情况的可能性更大一些？

A．先开枪的人死亡
B．后开枪的人死亡
C．上述两种情况的出现概率相同

或许有些出人意料的是，这个题目的答案为 A 。为了算出双方存活的概率，我们只需要考虑所有 6 种可能的子弹位置即可。不妨用符号 ⊙ 来表示有子弹的弹槽，用符号 ○ 来表示空的弹槽。我们便能列出下面这张表：

• ⊙⊙⊙○○○ → 先开枪者死
• ⊙⊙○○○⊙ → 先开枪者死
• ⊙○○○⊙⊙ → 先开枪者死
• ○○○⊙⊙⊙ → 后开枪者死
• ○○⊙⊙⊙○ → 先开枪者死
• ○⊙⊙⊙○○ → 后开枪者死

可见，先开枪者死亡的概率高达 2/3 ，是后开枪者死亡概率的两倍。

可以算出，当转轮里位置相连的子弹数分别为 1 、 2 、 3 、 4 、 5 、 6 时，先开枪者死亡的概率分别为 1/2 、 2/3 、 2/3 、 5/6 、 5/6 、 1 。看来，并不是所有游戏都是先下手为强啊。

 

20．小明参加某电视台的选秀节目。 A 、 B 、 C 三位导师欣赏了小明的一番激情演唱后，需要投票决定小明能否晋级。小明的表演征服了 A 、 B 两位导师，每位导师都有 4/5 的概率投出赞成票，支持小明晋级。但 C 导师则犹豫不决，不知道该如何选择。怎么办呢？节目组给出了两种方案供小明选择。第一种方案是， A 、 B 两位导师独立作出决定， C 则抛掷一枚公正的硬币，如果硬币正面朝上，则晋级与否完全以 A 的决定为准，如果硬币反面朝上，则晋级与否完全以 B 的决定为准。第二种方案是，A 、 B 两位导师独立投出赞成票或反对票， C 则抛掷一枚公正的硬币，如果硬币正面朝上，则投出赞成票，如果硬币反面朝上，则投出反对票，最后晋级与否则取决于三人中的多数票。为了提高晋级的概率，小明应该选择哪种方案？

A．选择第一种方案
B．选择第二种方案
C．两种方案的晋级概率相同

这个题目的答案是 C 。两种方案中，小明晋级的概率是相同的，都是 4/5 。即使把题目中 4/5 这个比例换一换，答案也依旧如此。不妨假设 A 、 B 两位导师投出赞成票的概率都是 p ，那么第一种方案中小明晋级的概率显然是 (1/2) · p + (1/2) · p = p 。第二种方案呢？两位导师都投出赞成票的概率是 p² ，此时小明必然晋级； A 投出赞成票 B 投出反对票的概率是 p · (1 – p) ，此时小明有 1/2 的概率晋级（这取决于 C ）； A 投出反对票 B 投出赞成票的概率是 (1 – p) · p ，此时小明有 1/2 的概率晋级（这取决于 C ）；其他情况下小明都无法晋级。因此，第二种方案中小明晋级的概率为 p² + (1/2) · p · (1 – p) + (1/2) · (1 – p) · p ，化简的结果是一样的： p 。

 

21．小明上了几次象棋课，回到家得意地要和爸爸妈妈一比高低。爸爸说：“好啊，那我们来搞一次家庭挑战赛吧。比赛分三轮进行，爸爸妈妈将会作为你的对手轮番上场。如果你在任意连续的两轮比赛中获胜，你就能得到一大笔零花钱。对了，挑战赛开始前，你可以指定爸爸妈妈的出场顺序哦。”小明深知，战胜爸爸的概率更低，战胜妈妈的概率更高（事实上也的确如此）。为了提高得到零花钱的概率，小明应该怎样安排爸爸妈妈的出场顺序？

A．爸爸、妈妈、爸爸
B．妈妈、爸爸、妈妈
C．两种情况下得到零花钱的概率相同

这是一个非常经典的问题。你或许会觉得，方案 B 更好，因为小明会更多地面对较弱的对手。而实际上，这个题的答案是 A 。这背后有一个很简单的直觉：中间那个人一定不能太强，因为中间那场输了，整个儿就没机会了。

我们可以定量地分析一下。假设战胜爸爸的概率是 p ，战胜妈妈的概率是 q ，根据题目假设， p < q 。如果采用爸爸、妈妈、爸爸的顺序，则得到零花钱的概率等于赢了前两场输了最后一场的概率，加上赢了后两场输了第一场的概率，再加上三场都赢了的概率。最后结果是：

p · q · (1 – p) + (1 – p) · q · p + p · q · p = 2 · p · q – p² · q

类似地，如果采用妈妈、爸爸、妈妈的顺序，则得到零花钱的概率就是：

q · p · (1 – q) + (1 – q) · p · q + q · p · q = 2 · p · q – p · q²

由于 p < q ，因此前一个式子一定比后一个式子更大。

 

22．一架客机上有 100 个座位， 100 个人排队依次登机。第一个乘客把登机牌搞丢了，但他仍被允许登机。由于他不知道他的座位在哪儿，他就随机选了一个座位坐下。以后每一个乘客登机时，如果他自己的座位是空着的，那么他就在他自己的座位坐下；否则，他就随机选一个仍然空着的座位坐下。当最后一个人登机时，发生下面哪种情况的可能性更大一些？

A．他发现剩下的空位正好就是他的
B．他发现剩下的空位不是他的
C．上述两种情况的出现概率相同

你或许会以为情况 A 出现的概率很小，但实际上，这个概率是 50% 。换句话说，这个题目的答案是 C 。我们可以通过一些严格而复杂的计算来说明这一点，但在这里，我更愿意给出一些直观的解释。注意到，当最后一名乘客登机时，最后一个空位要么就是他的，要么就是第一个乘客的（其他的座位如果没被别人抢占，最终也会被它真正的主人占据）。这两个位置会面对 98 个人的选择，它们的“地位”是相等的，它们的“命运”是相同的，不存在哪个概率大哪个概率小的问题。因此，它们成为最后一个空位的概率是均等的。也就是说，最后一个人发现剩下的空位正好是他的，其概率为 50% 。

下面是另一个有趣的解释。我们可以把问题等价地修改为，如果一个人发现自己的座位被别人占据后，他就叫这个人重新去找一个位置，自己则在这里坐下。结果你会发现，真正在飞机上跑来跑去不断换座位的人其实只有一个，就是第一个人。我们可以干脆叫他直接站在旁边，等他后面的 98 个人全部入座后，他再选个座位坐下。容易看出，他选中的座位要么是他自己的，要么是最后一个人的，这各占 50% 的概率。因此，最后一个人上来之后，正好能对号入座的概率也就是 50% 。

 

23．在每一代的繁殖中，每个阿米巴原虫都有 2/3 的概率分裂成两个，有 1/3 的概率死亡（而不产生下一代）。初始时只有一个阿米巴原虫，那么下面哪种情况的可能性更大一些？

A．阿米巴原虫在有限代之后灭绝
B．阿米巴原虫无限地繁殖下去
C．上述两种情况的出现概率相同

注意到，这个问题是有意义的。阿米巴原虫要么在有限代之后灭绝，要么无限地繁殖下去。我们的问题就是，究竟发生哪种情况的可能性更大。

实际上，这个题的答案选 C 。不妨把一个阿米巴原虫能无限繁殖下去的概率设为 p 。初始时的那个阿米巴原虫怎样才能无限繁殖下去呢？首先，它得分裂为两个阿米巴原虫，这有 2/3 的概率；然后，其中至少一个阿米巴原虫要无限繁殖下去。于是，我们得到式子：

p = (2/3) · (1 – (1 – p)²)

其中， (1 – p)² 表示两个阿米巴原虫都没能无限繁殖下去的概率。把上面的式子当作一个关于 p 的一元二次方程，可解得 p = 0 或 p = 1/2 。舍去 p = 0 ，于是得到 p = 1/2 。这就说明， A 、 B 两种情况的出现概率是相同的。

为什么我们可以舍去 p = 0 呢？要想说服自己这一点，这还真不容易。下面是一个不严谨的思路。如果我们把每个阿米巴原虫分裂成两个的概率记作 p₀ （原题则相当于 p₀ = 2/3 时的特例），那么阿米巴原虫无限繁殖下去的概率 p 就会满足：

p = p₀ · (1 – (1 – p)²)

解得 p = 0 或 p = (2 · p₀ – 1) / p₀ 。那么， p 究竟是多少呢？注意到以下三点：

1. 当 p₀ = 1 时，问题的答案显然应该为 1 ；
2. 不管 p₀ 是多少，问题的答案显然都应该是正数；
3. 在 p₀ 连续变化的过程中，问题的答案也应该发生连续的变化（这个猜测是合理的，我们姑且假设它正确，不再进行论证）。

为了同时满足上述三点，只有这样一种可能：当 p₀ = 1/2 时，问题的答案为 0 ；当 p₀ < 1/2 时，舍去后面那个解，即问题的答案一直都是 0 ；当 p₀ > 1/2 时，舍去前面那个解，即问题的答案为 (2 · p₀ – 1) / p₀ 。

 

24．一斤白酒下肚后，我醉醺醺地来到了悬崖边上。如果我再往前迈一步，就会掉下悬崖。我每过一分钟都会往前或者往后迈一步，每次有 1/3 的概率往前迈一步，有 2/3 的概率往后迈一步。假设悬崖边是一条直线，我每步方向都严格垂直于悬崖边，且步长保持一致。如果我无限地走下去，那么下面哪种情况的可能性更大一些？

A．我在有限步之后将会掉下悬崖
B．我永远不会掉下悬崖
C．上述两种情况的出现概率相同

注意到，这个问题是有意义的。我要么在有限步之后掉下悬崖，要么永远不会掉下悬崖。我们的问题就是，究竟发生哪种情况的可能性更大。

实际上，这个题的答案也是 C 。不妨假设我在有限步之后将会掉下悬崖的概率为 p 。那么， p 等于多少呢？如果我第一步就往前迈，那就直接掉下去了。这有 1/3 的概率。在另外 2/3 的情况下，我的第一步是往后迈的。如果我最后还是掉下悬崖了，那么在此期间，我一定回过出发点。回到出发点，本质上就相当于往前净走一步，这和从出发点出发最终掉下去了一样，概率都是 p ；回到出发点后，要想真的掉下去，这又有一个 p 的概率。于是，我们得到：

p = 1/3 + (2/3) · p²

解得 p = 1/2 或 p = 1 。舍去 p = 1 ，于是得到 p = 1/2 。这就说明， A 、 B 两种情况的出现概率是相同的。

为什么我们可以舍去 p = 1 呢？这里，我们可以使用和上一题类似的思路。如果用 p₀ 代替题目中的 2/3 ，则上面的式子变为了：

p = (1 – p₀) + p₀ · p²

解得 p = (1 – p₀) / p₀ 或 p = 1 。为了保证连续性，当 p₀ > 1/2 时，我们需要舍去 p = 1 。

你或许已经发现了，这一题和上一题非常相似。进一步考察两个问题的答案，你还会有更惊人的发现：在有限步之后掉下悬崖的概率是 (1 – p₀) / p₀ ，因此永远不会掉下悬崖的概率是 1 – (1 – p₀) / p₀ = (2 · p₀ – 1) / p₀ 。这正是上一题中阿米巴原虫无限繁殖下去的概率的表达式。

其实，这两道题的本质就是完全一样的。让我们把阿米巴原虫数量的变化想象成是数轴上不断左右移动的点。刚开始，这个点在 x = 1 的位置。考虑某个阿米巴原虫：如果它分裂了，那么数轴上的点会向右移动一个单位，这有 2/3 的概率；如果它死亡了，那么数轴上的点会向左移动一个单位，这有 1/3 的概率。上一题就相当于是问，数轴上的点更有可能会在有限步之后到达 x = 0 的位置，还是更有可能永远都到不了 x = 0 的位置。如果你把数轴上的点左移右移想成是在悬崖外前进后退，把 x = 0 的位置想象成掉下悬崖的位置，这就瞬间变成这一题的背景了。

 

25．A 、 B 两支球队之间要打 100 场比赛。初始时，两支球队的经验值都为 1 。在每一场比赛中，两支球队各自的获胜概率与它们的经验值成正比，随后获胜一方的经验值将会加 1 。那么，当 100 场比赛全部打完之后，下面哪种情况的可能性更大一些？

A．球队 A 在所有 100 场比赛中全部获胜
B．球队 A 在所有 100 场比赛中恰好有 50 场获胜
C．上述两种情况的出现概率相同

这是一个强者愈强，弱者愈弱的过程，因此其中一支球队完胜另一支球队的概率并不会太低，两支球队最终打成平手的概率也并不会太高。事实上，两种情况发生的概率是相同的，都是 1/101 。也就是说，这个题目的答案是 C 。

让我们把 A 、 B 两支球队打比赛的过程进一步抽象成下面这样：从字符串 AB 出发，不断选择某个字母并把它分裂成两个。也就是说，初始时的字符串为 AB ，每一次你需要随机选择一个字母，如果选中了 A ，就把它变成 AA ，如果选中了 B ，就把它变成 BB 。第一次操作之后， AB 有可能变成 AAB ，也有可能变成 ABB ；如果第一次操作之后的结果是 AAB ，那么第二次操作之后，结果就会概率均等地变成 AAAB 、 AAAB 和 AABB 之一。容易看出，字母 A 、 B 数量增加的模式，与原问题中 A 、 B 两支球队经验值增加的模式是完全一致的，因而我们要求的概率值就等价地变为了： 100 次操作之后，字符串变成 AAA…AAB 的概率是多少，字符串变成 AA…AABB…BB （两种字母各半）的概率又是多少。下面我们来说明，这两个概率值都是 1/101 。

先来看一个似乎与此无关的东西：把 0 到 100 之间的数随机排成一行的另类方法。首先，在纸上写下数字 0 ；然后，把数字 1 写在数字 0 的左边或者右边；然后，把数字 2 写在最左边，最右边，或者 0 和 1 之间……总之，把数字 k 概率均等地放进由前面 k 个数产生的（包括最左端和最右端在内的）共 k + 1 个空位中的一个。写完 100 之后，我们就得到了所有数的一个随机排列。

现在，让我们假设初始时的字符串是 A⁰B ，并且今后每次分裂时，都在分裂得到的两个字母之间标注这是第几次分裂。也就是说，下一步产生的字符串就是 A¹A⁰B 或者 A⁰B¹B 之一。如果下一步产生的字符串是 A¹A⁰B ，那么再下一步产生的字符串就会是 A²A¹A⁰B 、 A¹A²A⁰B 、 A¹A⁰B²B 之一……联想前面的讨论，你会发现，第 100 次操作结束后，所有数字实际上形成了一个 0 到 100 的随机排列，也就是说最开始的数字 0 最后出现在各个位置的概率是均等的。因此，最右边那个位置上的数字就是 0 的概率是 1/101 ，正中间那个位置上的数字就是 0 的概率也是 1/101 。这其实就是我们要比较的那两个概率值。

 

26．从全体正整数中随机选出两个正整数，则下面哪种情况的可能性更大一些？

A．这两个正整数互质（没有大于 1 的公约数）
B．这两个正整数不互质（有大于 1 的公约数）
C．上述两种情况的出现概率相同

这个问题的说法很不严谨。我们给出一个更加严谨的叙述方法。让我们用 P_N 来表示，从 1 到 N 中随机取出两个正整数，它们互质的概率是多少。我们的问题就是，当 N 趋于无穷时， P_N 的值究竟是大于 1/2 ，等于 1/2 ，还是小于 1/2 。

这是一个非常非常经典的问题。下面是最常见的一种解法。假设我们从全体正整数中随机选出了两个正整数 a 、 b 。其中， a 能被 2 整除的概率是 1/2 ， b 能被 2 整除的概率是 1/2 。因而，它们都能被 2 整除的概率就是 1 / 2² 。反过来，它们不都能被 2 整除的概率就是 1 – 1 / 2² 。类似地，它们不都能被 3 整除的概率就是 1 – 1 / 3² ，它们不都能被 5 整除的概率就是 1 – 1 / 5² ……于是，它们互质的概率就是：

(1 – 1 / 2²) · (1 – 1 / 3²) · (1 – 1 / 5²) · (1 – 1 / 7²) …

注意，这里用到了一个假设：如果 p 和 q 是两个质数，那么能否被 p 整除和能否被 q 整除，这是互相独立的。事实上也确实如此：一个数能被 p 整除的概率是 1 / p ，一个数能被 q 整除的概率是 1 / q ；一个数能同时被两个质数 p 和 q 整除，当且仅当它能被 p · q 整除，其概率是 1 / (p · q)。

为了求出上面这个式子的值，我们考虑它的倒数。 1 – 1 / 2² 的倒数是 1 / (1 – 1 / 2²) ，而由无穷等比级数的求和公式（见本文中的第 4 题），它又可以被我们写成 1 + 1 / 2² + 1 / 2⁴ + 1 / 2⁶ + … 。类似地，其他几项也都变成了 1 + 1 / 3² + 1 / 3⁴ + 1 / 3⁶ + … ，1 + 1 / 5² + 1 / 5⁴ + 1 / 5⁶ + … ，等等。现在，想象一下，如果把所有的括号全都展开，把所有的项全都乘开来，会得到什么？我们会既无遗漏又无重复地得到所有的 1 / n² ！

  (1 + 1 / 2² + 1 / 2⁴ + 1 / 2⁶ + … ) · (1 + 1 / 3² + 1 / 3⁴ + 1 / 3⁶ + … )
  · (1 + 1 / 5² + 1 / 5⁴ + 1 / 5⁶ + … ) · …
= 1 + 1 / 2² + 1 / 3² + 1 / 4² + 1 / 5² + …

比方说， 40 = 2 × 2 × 2 × 5 ，那么等式右边的 1 / 40² 这一项，就是由等式左边的第一个括号里的 1 / 2⁶ ，乘以第二个括号里的 1 ，乘以第三个括号里的 1 / 5² ，乘以其余所有括号里的 1 得到的。

1 + 1 / 2² + 1 / 3² + 1 / 4² + 1 / 5² + … 究竟等于多少呢？我们来证明，它小于 2 。这是因为：

  1 + 1 / 2² + 1 / 3² + 1 / 4² + 1 / 5² + …
< 1 + 1 / (1 × 2) + 1 / (2 × 3) + 1 / (3 × 4) + 1 / (4 × 5) + …
= 1 + 1 – 1/2 + 1/2 – 1/3 + 1/3 – 1/4 + 1/4 – 1/5 + …
= 2

别忘了， 1 + 1 / 2² + 1 / 3² + 1 / 4² + 1 / 5² + … 是我们把所求的概率值取了倒数后的结果。因此，我们所求的概率值就应该大于 1/2 了。也就是说，这道题目的正确答案是 A 。

可以证明， 1 + 1 / 2² + 1 / 3² + 1 / 4² + 1 / 5² + … 实际上等于 π² / 6 。因此，任意两个正整数互质的概率就是 6 / π² ≈ 0.608 。神奇的数学常数 π 经常会出现在一些与圆形八竿子打不着的地方，比如我们之前提过的 Buffon 投针问题。而大家刚才看到互质概率问题，才是我觉得最为经典的例子之一。

 

这篇文章中的题目是我长期收集而来的。大部分题目都是非常经典的题目，它们可以在 The Colossal Book of Short Puzzles and Problems 、 Mathematical Puzzles: A Connoisseur’s Collection 、 Mathematical Mind-Benders 、 Problems for Mathematicians, Young and Old 、 40 Puzzles and Problems in Probability and Mathematical Statistics 、 Fifty Challenging Problems in Probability 等书中找到。有些题目是我很早以前就写过的，此处有所改写。部分文字直接摘自《浴缸里的惊叹： 256 道让你恍然大悟的趣题》。