为了随机地并且概率均等地生成一个 1 到 6 之间的整数,通常的做法就是抛掷一个正方体的骰子。不过,这并不是唯一的办法。如果你有一枚公正的、正反概率相同的硬币,以及一枚不公正的、正反概率之比为 1 : 2 的硬币,那么你也能概率均等地生成一个 1 到 6 之间的整数。首先抛掷那枚不公正的硬币,那么结果有 1/3 的概率是正面朝上,有 2/3 的概率是反面朝上。如果出现了正面朝上的情况,那么令 i = 1 ;如果出现了反面朝上的情况,那么就再抛掷那枚公正的硬币,掷出正面则令 i = 2 ,掷出反面则令 i = 3 。最后,再抛掷一次公正的硬币,如果正面朝上则令 j = 0 ,如果反面朝上则令 j = 3 。容易看出, i + j 的值有 1, 2, 3, 4, 5, 6 这六种可能,它们出现的概率是均等的,都是 1/6 。
有人或许会说,用硬币模拟骰子哪有那么复杂,只用一枚公正的硬币就能办到:连续抛掷三次硬币,并且规定掷出“正正正”代表数字 1 ,掷出“正正反”代表数字 2 ,“正反正”为 3 ,“正反反”为 4 ,“反正正”为 5 ,“反正反”为 6 ,掷出“反反正”和“反反反”则重来,这不就行了吗?不过,这种方法有一个局限性:它不能保证整个过程在有限步之内完成。而我们刚才的方法中,总的步骤数有一个上限:三步之内必然完成。
我们的问题是:是否对于所有的正整数 n ,都能找到两枚合适的硬币,使得借助它们便能在有限步之内概率均等地产生一个 1 到 n 之间的整数?
答案是肯定的。接下来,我们将会构造性地证明,不管 n 是多少,我们总能使用正反出现概率分别为 1:1 和 1:(n-1) 的两枚硬币,在有限的步数内达成目的。不妨先以 n = 11 时的做法为例,来说明我们的大致思路。
当 n = 11 时,首先把 1:1 的那枚硬币连续抛掷五次,这会出现 32 种等概率的正反组合,然后抛掷 1:10 的那枚硬币,出现正面和出现反面的概率分别为 1/11 和 10/11 。
抛完这六次硬币后,一共会产生 64 种不同的情况,其中 32 种情况出现的概率都是 (1/32) × (1/11) = 1/352 ,另外 32 种情况出现的概率则都是 (1/32) × (10/11) = 10/352 。我们可以在一个单位正方形里直观地表示出这 64 种情况:先用一系列横线把整个正方形划分成 32 个等宽横条,再在左起 1/11 的地方画一条竖线,把每个横条都分成 1:10 两份。图中的这 64 个区域就对应着可能出现的 64 种情况,每个区域的面积占整个正方形的多少,就表示与之对应的情况出现的概率是多少。我们可以把整个正方形看作是由 32 × 11 = 352 个小格子组成的,那么每个格子的面积都占整个正方形的 1/352 ,左边每个区域都只包含 1 个格子,右边每个区域则都包含 10 个格子。
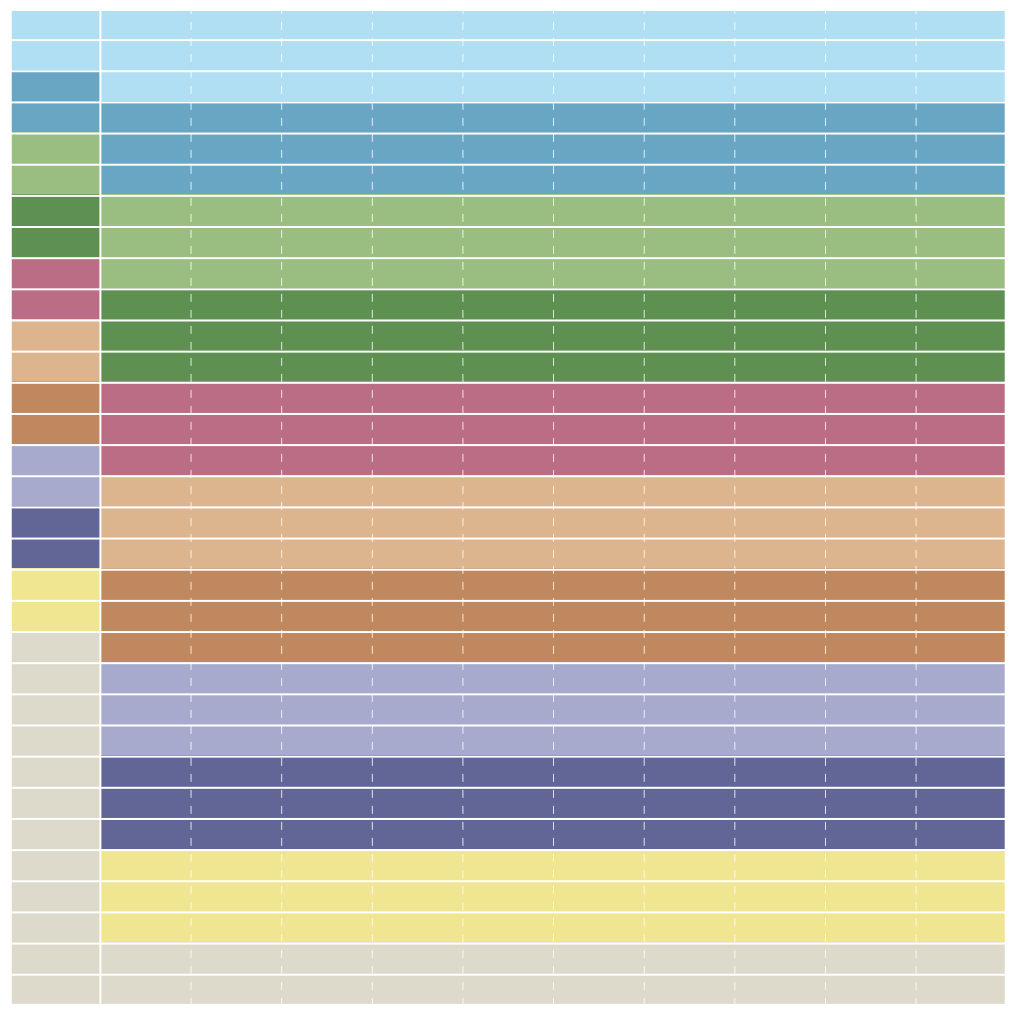
如果我们能把某些区域指派给数字 1 ,把另一些区域指派给数字 2 ,等等,最后把剩下的区域指派给 11 ,使得分给每个数字的区域都包含 32 个格子,即都占正方形总面积的 1/11 的话,问题就解决了。在上面这个图中,这件事情是可以办到的。每 2 个左边的区域和 3 个右边的区域加在一起,正好组成 32 个格子。这样推算下去,划分出 1, 2, 3, …, 10 的地盘,就会用掉左边的 20 个区域和右边的 30 个区域。最后,左边还剩下 12 个区域,右边还剩下 2 个区域,正好又组成了 32 个格子,它们正好成了 11 的地盘。像刚才所说的那样完成六次抛掷后,看看出现的情况位于哪个数的地盘里,便能等概率地产生 1 到 11 之间的整数了。
同样的思路可以适用于任意正整数 n 。取一枚公平的硬币并连续抛掷 k 次,再抛掷一枚正反概率为 1:(n-1) 的硬币,整个概率空间就被分成了 2k × 2 个区域,左边每个区域都占 1 小格,右边每个区域都占 n-1 小格,所有区域加在一起一共有 2k · n 个小格。我们的目标便是把这些区域重新组合成 n 份,使得每份正好都是 2k 个小格。令 q 等于 2k 除以 n-1 的商,令 r 等于 2k 除以 n-1 的余数,那么每次选择 q 个右边的区域和 r 个左边的区域相搭配,正好就是 2k 小格,可供 1 到 n 中的其中一个数使用。如果 q = r ,那么右边的区域和左边的区域会同时用完,于是大功告成。如果 q > r ,那么右边的区域会率先出现不够用的局面,不过这没有关系:右边的每一个区域都可以等效地用左边的 n-1 个区域来代替,因而不够的话总是能从左边找补回来的。如果 q < r 的话,这就真的不好办了,不过幸运的是,我们还留有一手:我们可以精心选择 k 的值,来避免 q < r 。
比方说,刚才 n = 11 时,我们选择的 k 值为 5 ,此时 2k 除以 n-1 的商 q = 3 ,余数 r = 2 。对于其他的正整数 n ,我们总能选择一个合适的 k ,使得 2k 除以 n-1 的商和余数满足 q ≥ r 吗?是的。我们至少可以这么做:注意到余数 r 始终小于除数 n-1 ,因此我们只需要让商数 q 至少是 n-1 即可;因而,选取足够大的 k ,使得 2k ≥ (n-1)2 ,便能保证 q ≥ r 了。