2008-04-22 4:32| 
13 Comments | 本文内容遵从 Stetson大学的一个非常可爱的MM（以后本Blog将简称她为Stetson MM）和我分享了一个很神奇的东西。她们正在做一个线性代数的课题研究，题目的大致意思是“用矩阵来构造分形图形”。Stetson MM叫我试着做下面这个实验：对于一个坐标点(x,y)，定义下面4个矩阵变换：
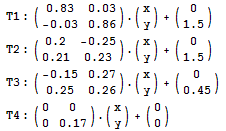
然后，初始时令(x,y)等于(0,0)，按照 T1 - 85%, T2 - 6%, T3 - 8%, T4 - 1% 的概率，随机选择一个变换对该点进行操作，生成的点就是新的(x,y)；把它画在图上后，再重复刚才的操作，并一直这样做下去。我心里觉得奇怪，这为什么会得到分形图形呢？于是我写了一个简单的Mathematica程序：
list = {{0, 0}};
last = {{0}, {0}};
For[i = 0, i < 50000, i++, r = Random[];
If[r < 0.85, last = {{0.83, 0.03}, {-0.03, 0.86}}.last + {{0}, {1.5}},
If[r < 0.91, last = {{0.2, -0.25}, {0.21, 0.23}}.last + {{0}, {1.5}},
If[r < 0.99, last = {{-0.15, 0.27}, {0.25, 0.26}}.last + {{0}, {0.45}},
last = {{0, 0}, {0, 0.17}}.last + {{0}, {0}}
]
]
];
list = Append[list, First[Transpose[last]]];
]
ListPlot[list, PlotStyle -> PointSize[0.002]]
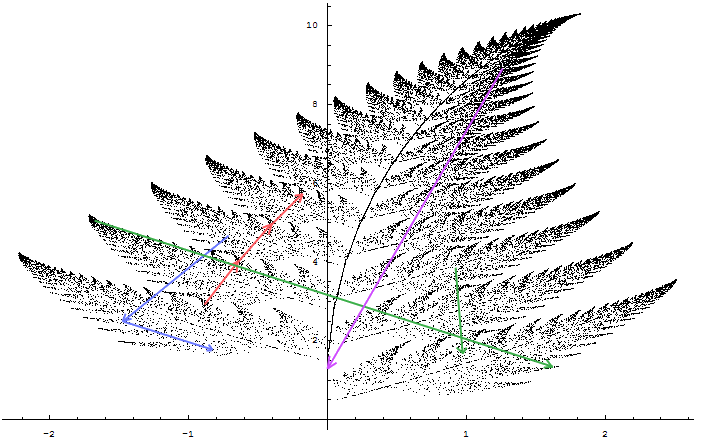
程序运行的结果真的是令我大吃一惊：竟然真的是一个分形图形！！我不禁再次对数学产生了一种崇敬和畏惧感！！
静下心来仔细研究了一下，其实这个东西的道理很简单：这些变换的实质就是把图形转移为另一个位置下的另一个尺度，经过变换以后的每个点都仍然在这个图形内。不同的变换有着不同的作用。T1的作用很明显：把该点移动到下一片小树叶上相同的位置。我们用红色的线条标注了对某个点连续三次T1变换的路径。T2, T3的作用是，把这个点在整个大叶子上的位置“投射”到最底部的叶片上对应的位置，其中T2负责投射到左边，T3负责投影到右边。我们分别用蓝色箭头和绿色箭头来演示T2和T3的轨迹。比如，对大叶片的左边第三叶的中间某个点进行T2变换，得到左边第一叶的左边第三个更小的叶片的中间；如果再进行一次变换，则就变到了左边第一叶的左边第一叶。T3的作用也基本上类似，我就不再多说了。最后， T4的作用是把某个点初始化到(0, 0.17y)，以后再经过一系列T1变换后就可以画出树叶中间的线条（的一部分）了，并等待某次T2或T3把该点变到最底层的叶片的中间线条上。有人会说，那这样变下去的话，岂不是所有点都只能在树叶中间的那根线条上？对！事实上，以后产生的每一个点都在某个“n级叶片”的中间那根线条上。
其实，我们之前是见过类似的东西的。例如，Sierpinski三角形也有相似的结论：给出三角形的三个顶点，然后从其中一个顶点出发，每次随机向任意一个顶点移动1/2的距离（走到与那个顶点的连线的中点上），并在该位置作一个标记；无限次操作后所有的标记就组成了Sierpinski三角形。
第500篇的沙发
4点……膜拜下
问下mathematica语言matrix67是在哪里学的
看来想做沙发一定要早啊
MM不是很漂亮到是很有味道
这个MM的Blog好像见过
Mathematica不是开源,我要赶紧删除.罚我我可负担不起
只能说……我什么都没看懂……
初三左右，我部文曲星就被人拿去做这类实验了～～
考虑买个Mathematica
我用matlab验证了一下，并估计了高度的增长趋势。
我觉得这就是生命--也许有一天，有机的生命形式会消失，但孕育于数学中的生命会一直存在下去。
你好，请问你的这段mathematica程序跑了多少时间？
我用mathematica6.0 需要跑很长很长时间。。。
不知道是不是哪里设置错了，我用C++写的代码很快就可以跑完了
还是因为mathematica本身就这么慢？
关于分形图形的几种最基本图形...
或许大家对分形还是没有最直观的概念，今天发几张基本分形图形（在go.....
[...] 用数学公式描绘自然界的图形，这就是分形的魅力把！这就是利用迭代绘出的树叶。按迭代公式绘制这个图的时候我发现和Matrix67的一篇内容完全一样..所以用了他的代码,换了迭代公式和次数一些的东西而已. [...]