最近沉迷于用 Mathematica 制作动画。受到这个动画的启发，我决定自己制作一些动画，来演示分形图形的进化过程。下面就是我这一周的成果。
分形
再谈Julia集与Mandelbrot集
很早以前，我简单介绍过 Julia 集和 Mandelbrot 集，文章在此。这可以说是数学中最神秘、最令人敬畏的研究对象之一。不过，那时我对这个话题了解还不太深。今天见到这个网页，让我对 Julia 集和 Mandelbrot 集有了更深的了解。我查阅了一些其他的资料，然后写下这篇长文，与大家一同分享。继续阅读以前，建议先看看我原来那篇文章（很短），那里面有很多漂亮的 Julia 集和 Mandelbrot 集的图片，这篇文章就不再展示了。
还是让我们先来简单复习一下复数吧。由于承认“负数也能开平方”将会带来很多幽雅和便利的结论，因此我们发明了虚数，用 i 来表示 -1 的平方根（即虚数单位），并把实数扩展为复数（即一切形如 a + b i 的数）。正如实数可以用数轴上的点来表示一样，复数可以用平面直角坐标系上的点来表示。令 x 轴表示复数的实数部分，令 y 轴表示复数的虚数部分，则 a + b i 就对应了平面上的点 (a, b) 。我们把这个平面直角坐标系叫做“复平面”。
经典证明：Cantor集中的元素两两相加可以遍历[0,2]
今天看到一个有趣的证明，来源在这里。
Cantor 集是一个简单而又神奇的分形图形。把 [0, 1] 三等分，挖去中间那一段（即挖去 (1/3, 2/3) ），然后把剩下两段也都分别进行三等分，并挖去各自中间的一段。这样无限地进行下去，最后得到的极限点集就是 Cantor 集了（上面那张图不是分割线，是 Cantor 集的一个示意图）。我们通常把 Cantor 集记作 C 。Cantor 集具有很多神奇的性质：它的 Lebesgue 测度为 0，但它却包含有不可数个点；它里面的每个点都不是孤点，但它却又是无处稠密的。你可以在这里看到一些具体的分析。
Cantor 集还有很多其他的性质。若 A 、 B 是两个集合，定义 A + B = {a + b | a ∈ A 并且 b ∈ B} ，也就是 A 中的某个元素与 B 中的某个元素相加可能得到的所有结果。下面我们将证明，C + C = [0, 2]。
兔年快乐，送大家分形兔子一只
考虑复数域上的迭代公式 zn+1 = zn^2 + (- 0.123 + 0.745 i) 。取不同的初始值 z0 ，迭代后 zi 的发散速度是不一样的。对于复平面上的每个点，以它为初始值的数列发散速度越快，就染越深的颜色表示；如果以它为初始值数列发散缓慢甚至收敛，则用相对较浅的颜色来表示。那么，整个图形将会是什么样子呢？本人纯手工打造 Mathematica 代码两行，为大家送上这幅神奇的图形：
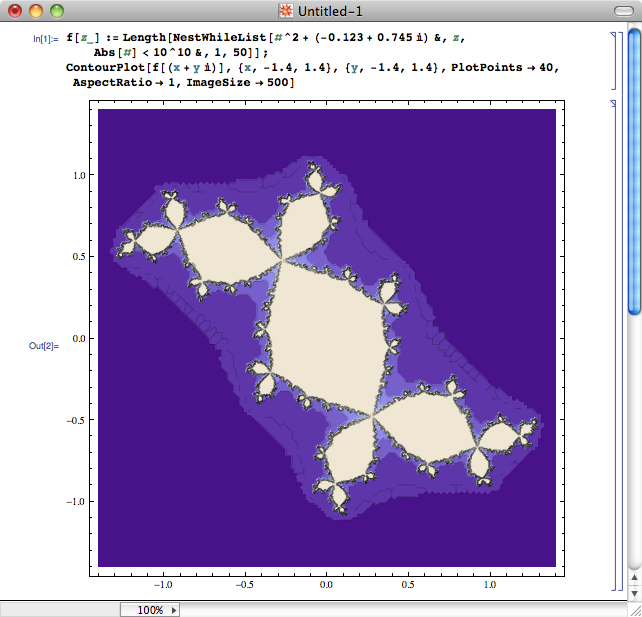
难以置信，简单的公式竟然生成了如此复杂的分形图形，看上去仿佛是大大小小的兔子竖着耳朵跳出来给大家拜年一样。这个图形叫做 Douady 兔子，是由法国数学家 Adrien Douady 发现的。它是一种 Julia 集。
徒手画分形图形，此MM乃神人也！
此 MM 叫做 Vi Hart 。她制作了一系列叫做 Doodling in Math Class 的视频，在 YouTube 上的观看人数都是好几万。在欣赏其无比强大的画图能力的同时，你也将会从一个全新的角度体验到数学的美妙。
Doodling in Math Class – Infinity Elephants