有一根不均匀的绳子，烧完正好需要 1 个小时。如何用这根绳子测出半个小时的时间呢？答案很巧妙：把这根绳子的两头同时点燃，绳子烧完时正好就过了半个小时。更妙的是下面这个加强版：如何用两根这样的绳子来计时 45 分钟？答案是，把其中一根绳子的两头都点燃，同时点燃另一根绳子的其中一头；待到前一根绳子烧完之后，再把第二根绳子的另一头也点燃，于是便能测出 30 + 15 = 45 分钟了。
一个有趣的问题自然而然地产生了：假如这样的绳子足够多，哪些时间能够用烧绳子的方法测出来呢？
为了解决这一问题，让我们先把这个问题本身理清楚——“烧绳子测量时间”的“游戏规则”究竟是什么？首先，一根绳子（的任意一头）可以在第 0 时刻或者另外某根绳子烧完的瞬间点燃。另外我们假设，在同一时刻，我们可以同时点燃任意多根绳子。而由此测出的时间段则定义为从点燃第一根绳子到最后一根绳子烧完的总时间。
用形式化的语言来描述，如果绳子两端分别在第 a 时刻和第 b 时刻点燃（其中 |a – b| < 1 ），那么绳子最终将在 (a + b + 1)/2 时刻烧尽。我们说某个时间点 x 是可以到达的，当且仅当存在两个可以到达的时间 a 、 b ，使得 x = (a + b + 1)/2 。显然，第 0 时刻是可以到达的。从第 0 时刻出发，不断用 (a + b + 1)/2 进行迭代，我们就能得到所有能够测出的时间了。
可以看到，随着迭代次数的增加，能够测量的时间越来越多，也越来越精确；不过，时间一去不复返，有些时间还是无法测量，绳子再多也没法弥补。
如果绳子充分多，能够测量的时间精确得吓人。最小的可测时间是 0 + 2^(-1) ，在时刻 1 之后最小的可测时间则是 1 + 2^(-3) ，超过 2 但最接近 2 的可测时间则是 2 + 2^(-10) 。
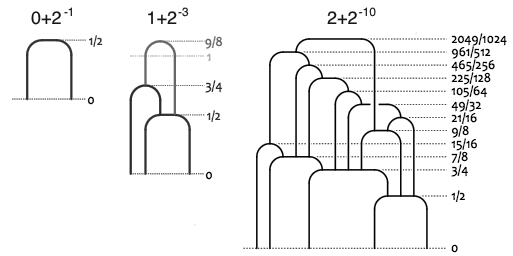
那么，在 3 之后最接近 3 的可测时间是 3 加上 2 的负多少次方呢？答案是 2 的 负 1 541 023 937 次方，可见烧绳子测量时间理论上有多精确。序列 1, 3, 10, 1 541 023 937 的增长速度之惊人，甚至可以说已经超过了指数级增长。那么，序列的下一项有多大呢？这个下一项真的可以说是大到难以想象了。即使说它有多少位，或者它的位数有多少位，也不能描述出它的大小。这个数必须用一些特殊的数学记号来表示，它大到甚至可以和 Graham 数 相提并论。
具体的一些结果还可以看这里：
http://mathpuzzle.com/fusible.pdf
大牛这么晚了还来更新~
板凳诶……
话说这儿还真有半夜来看的啊…
大牛你的图片都是用哪个软件画的啊…
好像没有考虑绳子只点燃一头的情况啊。不过修正也很简单，只要允许|a-b|=1就行了。不影响结论。
1/2能测出来，1/4就也能测了，1/8也能。。。。
@楼上: 绳子是不均匀的，1/4测不出来的
哈哈，The On-Line Encyclopedia of Integer Sequences上居然都没有 1, 3, 10, 1 541 023 937 这个序列
三体3里就有这个问题，^_^
首次抢到楼
这东西能不能烧了一段时间后才开始计时……？
@10楼：不能，因为你不知道它已经烧了多久
只要把一根绳子从两头和中间同时点燃，绳子会从中间烧断，这样绳子就变成了两根两头都被点燃的绳子，当有一条燃完后再迅速点燃另一根的中间，循环下去，理论上可以测出1/4，不过论可操作性的话就。。。
有一根不均匀的绳子，烧完正好需要 1 个小时。
这个假设有问题。。。
这并不意味着从两头烧就是30分钟啊。。。
非常有意思的题目啊。
谢谢，学习了
从两头烧就是30分钟，没有问题。
12楼
12a楼
14楼
这是blog服务器本身的玩意还是说m67迷信这个？
这个问题在大刘的《三体三-死神永生》里也问过，问的是测15分钟的。当时是一群小学生里只有三个能逃命 艾AA问了三个问题 答上来的就选他上飞船逃走。。。这是其中一个
12a。。。16楼说的对啊 都没在意 。。。
@12楼：附件那个pdf里更清晰地定义了游戏规则，这个是违反规则的
为什么不能这样呢：比如两根绳子，其中一根两头点燃，另一根一头点燃，第一根烧完之后立刻将第二根灭掉。这样就能得到剩下半小时的绳子。理论上，在快要接近1.0小时的时候，能得到无限短的绳子，也就是1.0左侧是无限稠密的。这样，将熄灭的绳子在1.0时刻重新燃起，不就能在1.0右侧复制出左侧的时刻了吗？
也就不存在“时刻 1 之后最小的可测时间则是 1 + 2^(-3) ”了。如果绳子一旦点燃就无法熄灭，当我白说。
#10 maa04,11 Maigo,19 morrowind:还有一点：原题要求从点燃第一根绳子起开始计时；如果允许从某根绳子烧完开始计时，那么任意小的时间间隔都可测出。
#地板 Maigo：1=1/2~1/2=(1/2+1/2+1)/2，见原文。一般地，在a时刻点燃一头相当于a->a+1，这可由b=a~a=(a+a+1)/2=(2a+1)/2,b~b=a+1来实现。原文的处理方式似乎使得形式更为统一，分析更为简单。
不过不得不说，作者得到的所有可测数的序类为epsilon_0这一事实、以及这个迅速增长的序列，都还是很有意思的。
@biohu 恩 之前想错了。。。
maxtrix大神，求这个问题在mathmatic的程序
大牛能不能介绍几本平面几何书
满地打滚求更新
请问那个pdf里面，关于margin的那一页上面的递推公式是不是有误？后面的code也出现了没有定义的函数margin2
不好意思，看错了。请教那个递推公式是怎么得到的
@19楼 说得对
听说今天是圣诞节，不知道我给博主评论我的枯木博客会收到什么礼物？祝博主，开心多一点
高智商的题啊
即使不能熄灭,1的左侧也应该是可以无穷接近的啊.假设N是1左侧的某个点,N可测.那么在0点燃一根绳的一端,时间到N的时候点燃它的另一端,这就得到了(1-N)/2的时间点.同理可得(1-(1-N)/2)/2.那就可以无限接近1了.
计算出来的1.X小时 1.X-1=0.X 就是从1个小时完结的时候开始计时 可以计算出来0.X小时 于是经过N次加减 理论上所有时间都可以计算出来 只是实际上……正如文末
恩 俩点间是这样的 有道理！
能测到什么呢？
32楼说法不对，按规则，不能在时间到N时才开始计时，因为绳子必须在开始计时后或开始计时的瞬间才能点燃。
比如两根绳子，其中一根两头点燃，另一根一头点燃，第一根烧完之后立刻将第二根灭掉。这样就能得到剩下半小时的绳子
今年的圣诞节也快到了，祝大家圣诞快乐
精彩~ 我有个问题，这些递归定义的数的集合是不是良序的，即每个数后面（即比这个数大）都存在一个最小的数？
恐怕很快不仅仅是和graham数相提并论了。
这个数列不是常规的那种通过正常的计算得到的，而是从无穷中抽出有限来
如果碰巧因为增长太快而不可计算的话，这伙计就可以直接拿去和繁忙海狸函数比较了，graham数什么的弱爆了
值得一提的是，这个数列的存在性并不是显然的，需要证明，很明显这篇日志没有注意到这一点
求大神证明这个数列存在……
燃烧速度不可能一样的，空想