目前,我正在《新知客》杂志上主持一个趣题栏目。每月杂志发行后,我将在 Blog 上同步更新。点击 这里 可以查看往期题目。
推理
1. 在每一个小题中,我们都按照某种属性把 26 个字母分成了两组。请你找出每个小题中的分组依据。
(1) CEFGHIJKLMNSTUVWXYZ ABDOPQR
(2) AEFHIKLMNTVWXYZ BCDGJOPQRSU
(3) COPSUVWXZ ABDEFGHIJKLMNQRTY
(4) ABCDEFGQRSTVWXZ HIJKLMNOPUY
(5) CDILMVX ABEFGHJKNOPQRSTUWYZ
2. 在面临二选一的情形犹豫不决时,很多人喜欢用抛硬币来解决问题。但是,由于硬币的两侧轻重不一,因此正反两面出现的几率并不是绝对均等的。这样的话,我们还能让硬币来帮助我们做决定吗?于是就有了下面这个有趣的问题:
假如你手中有一枚不公平的硬币,其中一面朝上的概率更大一些(但是你不知道具体大了多少)。你能想办法用这枚硬币“模拟”出一枚公平的硬币吗?
计算
1. 一根棍子的左端有 6 只间隔相等的蚂蚁,它们正以一个相同的速度向右爬行;棍子的右端也有 6 只蚂蚁,它们也在以同样的速度向左爬行。如果两个蚂蚁相向而行撞在了一起,它们会同时掉头往回爬行。如果某只蚂蚁爬出了棍子的端点,它会从棍子上掉下去。请问,到所有的蚂蚁都掉下棍子的时候,蚂蚁与蚂蚁之间一共发生了多少次碰撞?

2. 有这么一种赌博游戏:玩家选择 1 到 6 之间的一个数,并下 1 块钱的赌注。然后,庄家同时抛掷三颗骰子。如果这三颗骰子中都没有你选的数,你将输掉那 1 块钱;如果有一颗骰子的点数是你选的数,那么你不但能收回你的赌注,还能反赢 1 块钱;如果你选的数出现了两次,你将反赢 2 块钱;如果三颗骰子的点数都是你选的数,你将反赢 3 块钱。
这个赌博游戏对玩家有利还是对庄家有利?
填图
1. 左图的每个小方格内都填了一个不同的数,神奇的是方阵中的每一行、每一列和两条对角线上的三个数之和都相等(都等于 15 )。现在,你能否在右图的每个小方格内填入一个不同的数(不一定是九个连续的数),使得方阵中的每一行、每一列和两条对角线上的三个数之乘积都相等?
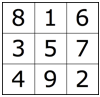
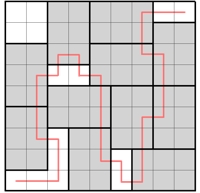
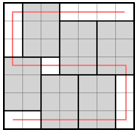
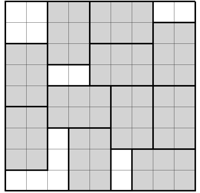
2. 从最左下角的小方格出发,画出一条到达右上角的路径。你的路径必须要经过每个灰色2×3方格中的其中两个小格。左图是一个示例。
推理
1. 在每一个小题中,我们都按照某种属性把 26 个字母分成了两组。请你找出每个小题中的分组依据。
(1) CEFGHIJKLMNSTUVWXYZ ABDOPQR
(2) AEFHIKLMNTVWXYZ BCDGJOPQRSU
(3) COPSUVWXZ ABDEFGHIJKLMNQRTY
(4) ABCDEFGQRSTVWXZ HIJKLMNOPUY
(5) CDILMVX ABEFGHJKNOPQRSTUWYZ
答案:(1) 字母中是否含有封闭区域 (2) 字母是否仅由直线笔划组成 (3) 字母的大小写形状是否一样 (4) 打字时用左手按键还是用右手按键 (5) 是否为罗马数字所用的字母
2. 在面临二选一的情形犹豫不决时,很多人喜欢用抛硬币来解决问题。但是,由于硬币的两侧轻重不一,因此正反两面出现的几率并不是绝对均等的。这样的话,我们还能让硬币来帮助我们做决定吗?于是就有了下面这个有趣的问题:
假如你手中有一枚不公平的硬币,其中一面朝上的概率更大一些(但是你不知道具体大了多少)。你能想办法用这枚硬币“模拟”出一枚公平的硬币吗?
答案:考虑连续抛掷两次硬币后的结果:如果结果是一正一反,那么先正后反和先反后正的概率一定是相同的(即使这枚硬币是不公平的)。借助这一点,我们就有了下面这个方案:连续抛掷两次硬币,如果两次抛掷的结果分别是“正”、“反”,就视作最终结果为“正”;如果两次抛掷的结果分别是“反”、“正”,就视作最终结果为“反”;如果是其它情况,就重新再来。
计算
1. 一根棍子的左端有 6 只间隔相等的蚂蚁,它们正以一个相同的速度向右爬行;棍子的右端也有 6 只蚂蚁,它们也在以同样的速度向左爬行。如果两个蚂蚁相向而行撞在了一起,它们会同时掉头往回爬行。如果某只蚂蚁爬出了棍子的端点,它会从棍子上掉下去。请问,到所有的蚂蚁都掉下棍子的时候,蚂蚁与蚂蚁之间一共发生了多少次碰撞?

答案: 36 次。我们不妨把两只蚂蚁相撞后双双调头往回走看作是它们互相穿过了对方的身体继续向前爬行,此时答案就很显然了。
2. 有这么一种赌博游戏:玩家选择 1 到 6 之间的一个数,并下 1 块钱的赌注。然后,庄家同时抛掷三颗骰子。如果这三颗骰子中都没有你选的数,你将输掉那 1 块钱;如果有一颗骰子的点数是你选的数,那么你不但能收回你的赌注,还能反赢 1 块钱;如果你选的数出现了两次,你将反赢 2 块钱;如果三颗骰子的点数都是你选的数,你将反赢 3 块钱。
这个赌博游戏对玩家有利还是对庄家有利?
答案:这个赌博游戏是真实存在的,它叫做“骰子掷好运” (Chuck-a-Luck) ,在美国很多赌场都能玩得到。对玩家而言,这个游戏看上去相当诱人:用三颗骰子掷出 6 个数中的一个,怎么也会有一半的概率砸中吧,那玩家起码有一半的时间是在赚钱,应当是稳赚不赔呀。这种直观的想法其实是错误的。一颗骰子的点数有 5/6 的概率不是你选的数,若三颗骰子的点数都不是你所选的数,其概率就应为 5/6 的 3 次方,大约是 57.87% 。也就是说,大多数时候你都是在赔钱的。
不过,考虑到赚钱时玩家有机会成倍地赢钱,这能否把输掉的钱赢回来呢?一些更为细致的计算可以告诉我们,即使考虑到这一点,游戏对玩家仍然是不利的:平均每赌 1 块钱就会让玩家损失大约 8 分钱。在这里,我们避免繁琐的计算,而是用一种简单而有趣的解释来说明,庄家的确是这个游戏的大赢家。
假设有 6 名玩家同时在玩这个游戏,这 6 个人分别赌 6 个不同的点数。抛掷骰子后,如果三颗骰子的点数都不一样,庄家赢 3 块亏 3 块;如果有两颗骰子点数一样,庄家赢 4 块亏 3 块;如果三颗骰子的点数全一样,庄家赢 5 块亏 3 块。也就是说,无论抛掷骰子的结果如何,庄家都不会赔钱!虽然一轮游戏下来有的玩家赚了,有的玩家亏了,但从整体来看这 6 名玩家是在赔钱的,因此平均下来每个玩家也是在不断输钱的。
填图
1. 左图的每个小方格内都填了一个不同的数,神奇的是方阵中的每一行、每一列和两条对角线上的三个数之和都相等(都等于 15 )。现在,你能否在右图的每个小方格内填入一个不同的数(不一定是九个连续的数),使得方阵中的每一行、每一列和两条对角线上的三个数之乘积都相等?
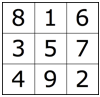

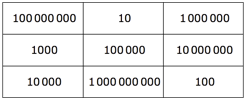
答案:满足要求的填法不是唯一的,但下面这个答案或许是最简单的一种。依次观察题目左图所给的方阵中的每个小方格:方格里的数是几,在新方阵的相应位置中就填入 1 后面加多少个 0 。显然,新方阵中的每一行、每一列和两条对角线上的三个数之乘积都是 1 后面 15 个 0 。
2. 从最左下角的小方格出发,画出一条到达右上角的路径。你的路径必须要经过每个灰色2×3方格中的其中两个小格。左图是一个示例。


答案: