2009-02-08 22:17| 
28 Comments | 本文内容遵从 概率论给我们带来了很多匪夷所思的反常结果，条件概率尤其如此。网络上每一次有人发帖提出与条件概率有关的悖论时，总会引来无数人的围观和争论，哪怕这些问题的实质都是相同的。
来看两道简单的组合数学问题：
1. 四个人打桥牌。其中一个人说，我手上有一个A。请问他手上有不止一个A的概率是多少？
2. 四个人打桥牌。其中一个人说，我手上有一个黑桃A。请问他手上有不止一个A的概率是多少？
这两个问题看起来很像，实际算法大不相同。在第一题问题中，
手上一个A也没有 有 C(48,13) 种情况
手上有至少一个A 有 C(52,13) - C(48,13) 种情况
手上恰好有一个A 有 C(48,12) * 4 种情况
手上有至少两个A 有 C(52,13) - C(48,13) - C(48,12) * 4 种情况
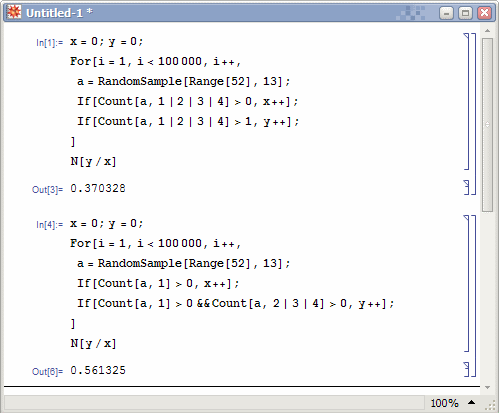
根据条件概率公式，手上有超过一个A的概率为(C(52,13) - C(48,13) - C(48,12) * 4) / (C(52,13) - C(48,13)) = 5359/14498 ≈ 37%
在第二个问题中，
手上有黑桃A 有 C(51,12) 种情况
手上没有其它花色的A 有 C(48,12) 种情况
手上还有其它花色的A 有 C(51,12) - C(48,12) 种情况
根据条件概率公式，手上有超过一个A的概率为(C(51,12) - C(48,12)) / C(51,12) = 11686/20825 ≈ 56%
有趣的事情出来了：如果这个人宣布了手中A的花色，他手中有一个以上A的概率竟然会大大增加。
这怎么可能呢？难道我们上面的计算结果是错误的？事实上，上面的计算并没有错：
沙发……
回复再看……
看了……
茫然了……
去年夏天去杭州数学夏令营的时候，讲组合数学的教授上来就拿这个问题做引子来着~
很容易理解……
因为有至少2个A的时候，就更可能其中一个是黑桃A……
令我想起了三门问题
回地毯：我们的教授怎么没有说……
借地方问道做不出的题
乒乓球单打比赛，选手A对选手B。
已知如果选手A发球，得分概率是a (0<a<1)，如果接对方发球，得分概率是b (0<b<1)。
有两种规则可供选择：
第一种规则两人每小分轮流发球。
第二种规则胜利者可以继续发球，失球后对手发球。
先得到n分的选手胜利。例如n ＝ 11，任何选手的得分先达到11就赢了。
一开始A选手发球。（所以如果两人轮流得1分，最后A赢）
求证：对于任何的a, b, n，两种规则下A选手的胜率一样。
拿到任意花色A的概率比单一花色的A的概率高 所以分母大了显得所求概率低了
虽然我知道算出的结果肯定没错，但如何来理解这个结论？想不通啊。
因为有至少2个A的时候，就更可能其中一个是黑桃A……
所以反过来，有一个黑桃A的条件下至少2个A的概率也比有任意A时大。
就比如说，A代表去研究某个问题的4个人，黑桃A代表最先解决的一个，
那么最先解决某问题的研究所很可能人手比较足。
这个其实很好理解嘛，只有手上确实是黑桃A的时候，才可能宣布自己手上有黑桃A嘛。
看了两天突然发现原来这个人说的一定是真话...
如果一副牌升级时无条件抢亮主3，那么有黑桃3的人和有主3的人手上有不止一个3的概率哪个大？
不妨设c=1-a，d=1-b。
假设按照第一种规则打的时候把2*n-1局打满，那么每一个最终小结果概率的形式都会是一串a和c（共n个）的连乘积乘以一串b和d（共n-1个）的连乘积，而且A胜当且仅当a和b的个数加起来>=n。
现在，按照第二种规则打时，树形图不是满的，接下来我们不继续用第二种规则，而用另外的规则把它补满：在某个终端结点处，如果A胜剩下的都让B发球，B胜都让A发球。
这样，小结果就可以一一对应了。我们把第一种规则下的一个小结果写成两行，一行n个a和c（A发球），一行n-1个b和d（B发球），将其对应于第二种规则补满后的小结果：
从第一行开始读。每次读到a或d（发球胜）就接着读，读到c或b（接球胜）就转到另一行，开始读第一个没读过的。
读到一方胜利后，剩下的一列的结果依次当作最后“补满”比赛的结果。
这样必然恰好有一列读完，因为如果最后A胜，那么A开始发了一次球，最后赢了一个球，中间的发球/赢球对应，恰把n个发球对应n分；B开始不发球，易知只发球n-1次。
接下来的证明就十分简单了。
理解起来还行吧
如果这个人宣布手里有黑桃A，那么剩下不多于三个A在另外三家的，肯定不会包括黑桃A了。
如果这个人宣布手里有A，那么剩下不多于三个A在另外三家的，却要在四个A里面随机。
稍微改一下：
四个人打桥牌。其中一个人说，我手上有一个A，并且说出来这个A的花色，请问他手上有不止一个A的概率是多少？
这是不是就跟第一个问题一样了？
不过如果他有2个A的话，“我有A”这句话只能说一遍
但是“我有黑桃A，我有红桃A”可以说两遍
18楼和问题1是一样的。问题2的主要不同就在于只能声明黑桃 而不能是其它花色 所以文章末段“ 有趣的事情出来了：如果这个人宣布了手中A的花色，他手中有一个以上A的概率竟然会大大增加。”是模糊的表达
其实这个问题让人混淆的原因在于概率被约分了，掩盖了本来庞大的情况总数。
.................................
不能说：如果这个人宣布了手中A的花色，他手中有一个以上A的概率竟然会大大增加。
参考那个门后边有羊的问题，概率不能简单的根据情况数算
.................................
如果你问他，是否有黑桃A，他说有，那结果应该按照第二种方法算
但是如果他宣布有至少一个A，之后再宣布有黑桃A，那概率不会变
因为他是从他有A之中选出一个宣布的，如果没有黑桃A，他不会宣布自己没有黑桃A，而是随便再宣布一个别的
.................................
请问，概率论有什么经典的教材吗？
典型的信息博弈，打牌双方的信息时不对称的，的确可以作为欺骗手段的！
[...] 3. 一个人有两个小孩儿，其中有一个生于星期二的男孩儿。问另一个是男孩儿的概率是多少？ 答案：13/27。这是“已知有一个男孩儿，问另一个是男孩儿的概率”的加强版，是一个非常精彩的条件概率问题。它非常直观地告诉我们，事先提供更准确的信息能给概率带来怎样的变化。另一个有趣的问题见这里。 [...]
20楼Jack点出了问题关键
就是说，如果游戏一开始大家规定好，四人中任何一人拿到黑桃A，就喊：“我拿到了黑桃A”，那么当某人喊出来时，他有两张以上的概率为56%
但是如果游戏一开始只是规定，四人中任何一人只要拿到A，就喊：“我拿到了A”并宣布花色，这样当某人喊出来时，他有两张以上的概率就只有37%
如果有人不懂，可以把命题简化一下，就用两张A，两张K来计算就可以了，组合分别为A1A2,A1K1,A1K2,A2K1,A2K2,K1K2,
如果只说有A，那么就是1/5，如果说有A1,那么就是1/3。