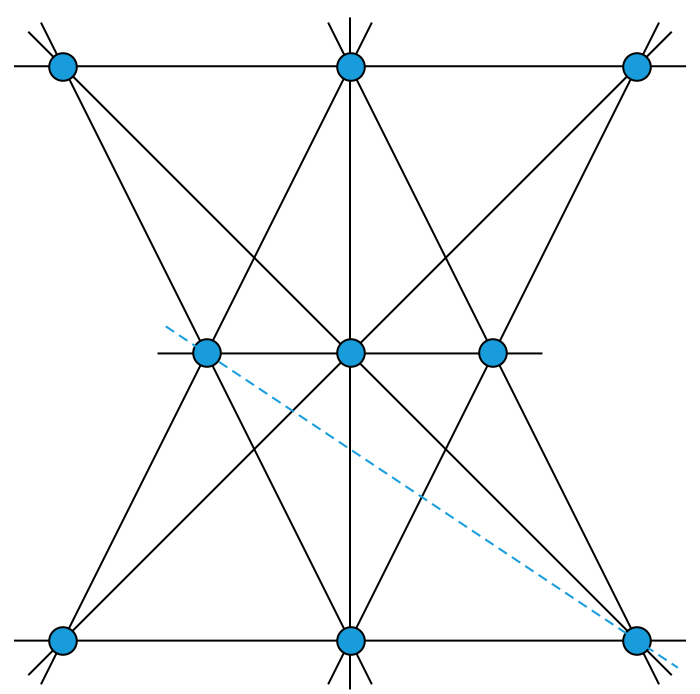
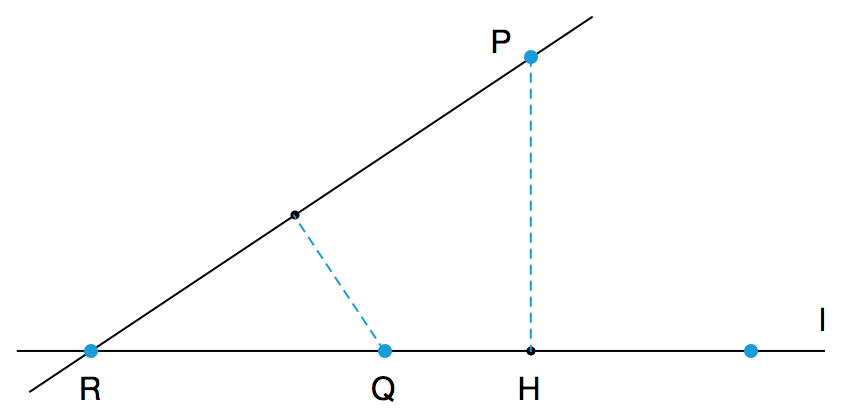
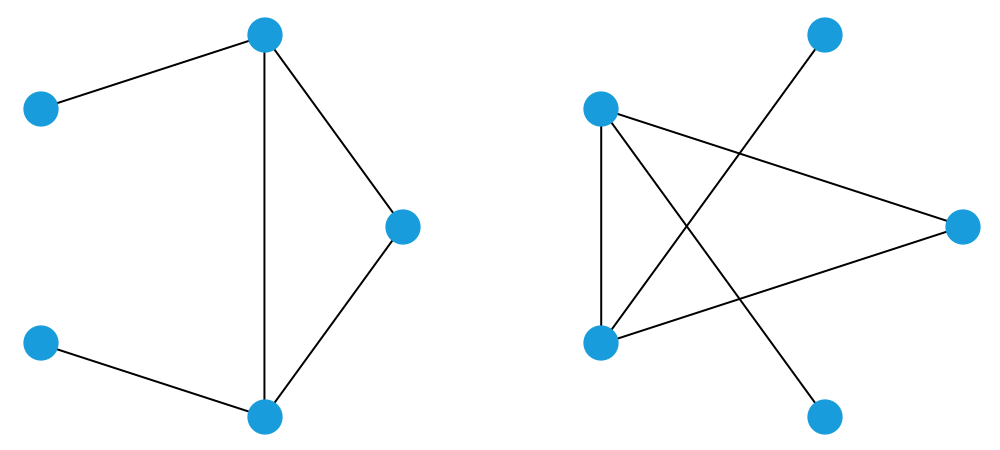
若干个顶点以及某些顶点和顶点之间的连线,就构成了一个“图”。如果对某个图进行变换,使得原来任意两个有连线的顶点之间都不再有连线,原来任意两个没有连线的顶点之间现在都有连线了,那么所得到的图就是原来那个图的“补图”。如果一个图和它的补图具有本质上完全相同的结构(这意味着,把其中一个图的顶点以适当的方式与另一个图的顶点建立一一对应的关系,那么对于谁和谁之间有连线、谁和谁之间没有连线这样的问题,两个图的情况是完全一样的),我们就说这个图和它自己是互补的。下图显示了一个顶点数为 5 的图以及它的补图,容易看出,它们的本质结构是相同的。这说明,顶点数为 5 的图有可能和自己互补。
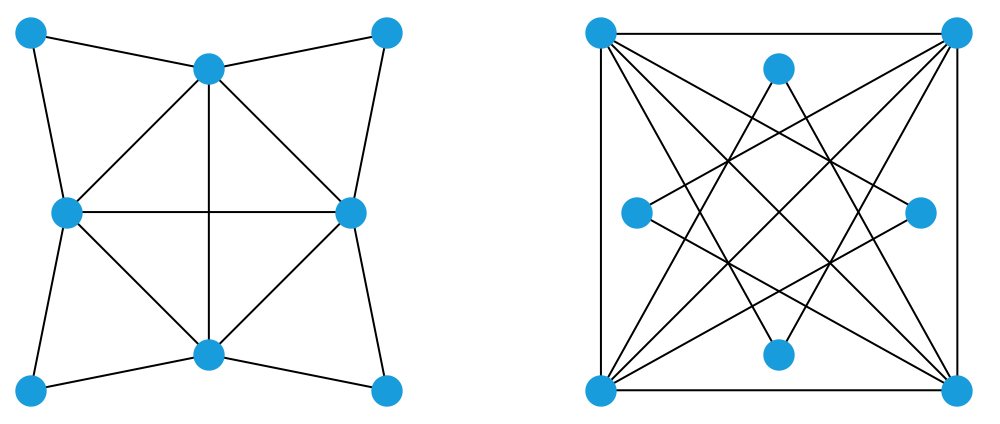
下图显示了一个顶点数为 8 的图,它和它的补图也具有同样的本质结构(你能看出来吗)。这说明,顶点数为 8 的图也有可能和自己互补。
我们今天的问题是:对于那些正整数 n ,存在顶点数为 n 的与自己互补的图?