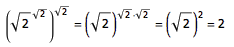数论,数学中的皇冠,最纯粹的数学。早在古希腊时代,人们就开始痴迷地研究数字,沉浸于这个几乎没有任何实用价值的思维游戏中。直到计算机诞生之后,几千年来的数论研究成果突然有了实际的应用,这个过程可以说是最为激动人心的数学话题之一。最近我在《程序员》杂志上连载了《跨越千年的 RSA 算法》,但受篇幅限制,只有一万字左右的内容。其实,从数论到 RSA 算法,里面的数学之美哪里是一万字能扯完的?在写作的过程中,我查了很多资料,找到了很多漂亮的例子,也积累了很多个人的思考,但最终都因为篇幅原因没有加进《程序员》的文章中。今天,我想重新梳理一下线索,把所有值得分享的内容一次性地呈现在这篇长文中,希望大家会有所收获。需要注意的是,本文有意为了照顾可读性而牺牲了严谨性。很多具体内容都仅作了直观解释,一些“显然如此”的细节实际上是需要证明的。如果你希望看到有关定理及其证明的严格表述,可以参见任意一本初等数论的书。把本文作为初等数论的学习读物是非常危险的。最后,希望大家能够积极指出文章中的缺陷,我会不断地做出修改。
======= 更新记录 =======
2012 年 12 月 15 日:发布全文。
2012 年 12 月 18 日:修改了几处表达。
2021 年 9 月 13 日:根据 Chang 的指正做了修改。
======== 目录 ========
(一)可公度线段
(二)中国剩余定理
(三)扩展的辗转相除
(四)Fermat 小定理
(五)公钥加密的可能性
(六)RSA 算法