经典证明：几乎所有有理数都是无理数的无理数次方

    一个无理数的无理数次方是否有可能是一个有理数？这是一个非常经典的老问题了。答案是肯定的，证明方法非常巧妙：考虑根号 2 的根号 2 次方。如果这个数是有理数，问题就已经解决了。如果这个数是无理数，那么就有：

      

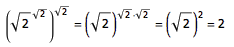
    我们同样会得到一个无理数的无理数次方是有理数的例子。

    这是一个典型的非构造性证明的例子：我们证明了无理数的无理数次方有可能等于有理数，但却并没有给出一个确凿的例子。毕竟我们也不知道，真实情况究竟是上述推理中的哪一种。那么，真实情况究竟是上述推理中的哪一种呢？ Gelfond-Schneider 定理告诉我们，假设 α 和 β 都是代数数，如果 α 不等于 0 和 1 ，并且 β 不是有理数，那么 α 的 β 次方一定是超越数。根据这一定理我们可以立即看出，根号 2 的根号 2 次方真的是一个无理数，实际情况应该是上述推理中的后者。

    那么，是否存在一个无理数 a ，使得 a 的 a 次方是有理数呢？最近， Stan Dolan 证明了这样一个结论：事实上，几乎所有 (1, ∞) 里的有理数都是某个无理数 a 的 a 次方。


    注意到当 x 大于 1 时，函数 f(x) = xx 是连续单调递增的，因而对于所有 (1, ∞) 里的有理数 r ，一定存在唯一的 a ，使得 aa = r 。不妨假设 a 是一个有理数，它的最简分数形式是 n / m 。如果 m = 1 ，那么我们会有平凡解 nn = r 。下面我们证明， m 是不可能大于 1 的，否则会产生矛盾。

    假设有理数 r 的最简分数形式是 c / b ，于是我们有：

      (n / m)n / m = c / b

    或者说：

      nn · bm = mn · cm

    注意到， mn 是 nn · bm 的约数。然而， m 和 n 是互质的， mn 与 nn 没有公共因子，因而 mn 一定是 bm 的约数。同理， bm 是 mn · cm 的约数，但由于 b 和 c 是互质的，因此 bm 一定是 mn 的约数。 mn 和 bm 怎么可能互为对方的约数呢？只有一种可能，就是 mn 等于 bm 。

    既然 mn = bm ，说明 m 和 b 肯定有大于 1 的公因数。假设 p 是 m 和 b 的某个公共质因数。我们把 m 和 b 中的所有质因数 p 都提出来，将它们写成 m = pi · k 和 b = pj · l ，其中 k 和 l 都不再含有质因数 p 。于是， mn = bm 就可以重新写为：

      pi·n · kn = pj·m · lm

    既然 mn 是等于 bm 的，它们一定含有相同数量的质因数 p ，因而 i·n = j·m ，可知 m 是 i·n 的约数。但是 m 和 n 是互质的，因此 m 一定是 i 的约数。最后，注意到 pi 是 m 的约数，从而也就是 i 的约数。于是矛盾产生了：由于 p ≥ 2 ，因此 pi 一定严格地大于 i ，不可能是它的约数。

    因此，对于所有大于 1 的有理数，除非它恰好等于某个整数 n 的 n 次方，否则它都将是某个无理数 a 的 a 次方。

 
来源：http://www.mathteacherctk.com/blog/2012/04/a-representation-of-rational-numbers/

38 条评论

发表评论

2  ×  2  =