数论，数学中的皇冠，最纯粹的数学。早在古希腊时代，人们就开始痴迷地研究数字，沉浸于这个几乎没有任何实用价值的思维游戏中。直到计算机诞生之后，几千年来的数论研究成果突然有了实际的应用，这个过程可以说是最为激动人心的数学话题之一。最近我在《程序员》杂志上连载了《跨越千年的 RSA 算法》，但受篇幅限制，只有一万字左右的内容。其实，从数论到 RSA 算法，里面的数学之美哪里是一万字能扯完的？在写作的过程中，我查了很多资料，找到了很多漂亮的例子，也积累了很多个人的思考，但最终都因为篇幅原因没有加进《程序员》的文章中。今天，我想重新梳理一下线索，把所有值得分享的内容一次性地呈现在这篇长文中，希望大家会有所收获。需要注意的是，本文有意为了照顾可读性而牺牲了严谨性。很多具体内容都仅作了直观解释，一些“显然如此”的细节实际上是需要证明的。如果你希望看到有关定理及其证明的严格表述，可以参见任意一本初等数论的书。把本文作为初等数论的学习读物是非常危险的。最后，希望大家能够积极指出文章中的缺陷，我会不断地做出修改。

======= 更新记录 =======

2012 年 12 月 15 日：发布全文。
2012 年 12 月 18 日：修改了几处表达。
2021 年 9 月 13 日：根据 Chang 的指正做了修改。

======== 目录 ========

（一）可公度线段
（二）中国剩余定理
（三）扩展的辗转相除
（四）Fermat 小定理
（五）公钥加密的可能性
（六）RSA 算法

 
 
（一）可公度线段

    Euclid ，中文译作“欧几里得”，古希腊数学家。他用公理化系统的方法归纳整理了当时的几何理论，并写成了伟大的数学著作《几何原本》，因而被后人称作“几何学之父”。有趣的是，《几何原本》一书里并不全讲的几何。全书共有十三卷，第七卷到第十卷所讨论的实际上是数论问题——只不过是以几何的方式来描述的。在《几何原本》中，数的大小用线段的长度来表示，越长的线段就表示越大的数。很多数字与数字之间的简单关系，在《几何原本》中都有对应的几何语言。例如，若数字 a 是数字 b 的整倍数，在《几何原本》中就表达为，长度为 a 的线段可以用长度为 b 的线段来度量。比方说，黑板的长度是 2.7 米，一支铅笔的长度是 18 厘米，你会发现黑板的长度正好等于 15 个铅笔的长度。我们就说，铅笔的长度可以用来度量黑板的长度。如果一张课桌的长度是 117 厘米，那么 6 个铅笔的长度不够课桌长， 7 个铅笔的长度又超过了课桌长，因而我们就无法用铅笔来度量课桌的长度了。哦，当然，实际上课桌长相当于 6.5 个铅笔长，但是铅笔上又没有刻度，我们用铅笔来度量课桌时，怎么知道最终结果是 6.5 个铅笔长呢？因而，只有 a 恰好是 b 的整数倍时，我们才说 b 可以度量 a 。

    给定两条长度不同的线段 a 和 b ，如果能够找到第三条线段 c ，它既可以度量 a ，又可以度量 b ，我们就说 a 和 b 是可公度的（ commensurable ，也叫做可通约的）， c 就是 a 和 b 的一个公度单位。举个例子： 1 英寸和 1 厘米是可公度的吗？历史上，英寸和厘米的换算关系不断在变，但现在，英寸已经有了一个明确的定义： 1 英寸精确地等于 2.54 厘米。因此，我们可以把 0.2 毫米当作单位长度，它就可以同时用于度量 1 英寸和 1 厘米： 1 英寸将正好等于 127 个单位长度， 1 厘米将正好等于 50 个单位长度。实际上， 0.1 毫米、 0.04 毫米 、 (0.2 / 3) 毫米也都可以用作 1 英寸和 1 厘米的公度单位，不过 0.2 毫米是最大的公度单位。

    等等，我们怎么知道 0.2 毫米是最大的公度单位？更一般地，任意给定两条线段后，我们怎么求出这两条线段的最大公度单位呢？在《几何原本》第七卷的命题 2 当中， Euclid 给出了一种求最大公度单位的通用算法，这就是后来所说的 Euclid 算法。这种方法其实非常直观。假如我们要求线段 a 和线段 b 的最大公度单位，不妨假设 a 比 b 更长。如果 b 正好能度量 a ，那么考虑到 b 当然也能度量它自身，因而 b 就是 a 和 b 的一个公度单位；如果 b 不能度量 a ，这说明 a 的长度等于 b 的某个整倍数，再加上一个零头。我们不妨把这个零头的长度记作 c 。如果有某条线段能够同时度量 b 和 c ，那么它显然也就能度量 a 。也就是说，为了找到 a 和 b 的公度单位，我们只需要去寻找 b 和 c 的公度单位即可。怎样找呢？我们故技重施，看看 c 是否能正好度量 b 。如果 c 正好能度量 b ，c 就是 b 和 c 的公度单位，从而也就是 a 和 b 的公度单位；如果 c 不能度量 b ，那看一看 b 被 c 度量之后剩余的零头，把它记作 d ，然后继续用 d 度量 c ，并不断这样继续下去，直到某一步没有零头了为止。

      

    我们还是来看一个实际的例子吧。让我们试着找出 690 和 2202 的公度单位。显然， 1 是它们的一个公度单位， 2 也是它们的一个公度单位。我们希望用 Euclid 的算法求出它们的最大公度单位。首先，用 690 去度量 2202 ，结果发现 3 个 690 等于 2070 ，度量 2202 时会有一个大小为 132 的零头。接下来，我们用 132 去度量 690 ，这将会产生一个 690 – 132 × 5 = 30 的零头。用 30 去度量 132 ，仍然会有一个大小为 132 – 30 × 4 = 12 零头。再用 12 去度量 30 ，零头为 30 – 12 × 2 = 6 。最后，我们用 6 去度量 12 ，你会发现这回终于没有零头了。因此， 6 就是 6 和 12 的一个公度单位，从而是 12 和 30 的公度单位，从而是 30 和 132 的公度单位，从而是 132 和 690 的公度单位，从而是 690 和 2202 的公度单位。

      

    我们不妨把 Euclid 算法对 a 和 b 进行这番折腾后得到的结果记作 x 。从上面的描述中我们看出， x 确实是 a 和 b 的公度单位。不过，它为什么一定是最大的公度单位呢？为了说明这一点，下面我们来证明，事实上， a 和 b 的任意一个公度单位一定能够度量 x ，从而不会超过 x 。如果某条长为 y 的线段能同时度量 a 和 b ，那么注意到，它能度量 b 就意味着它能度量 b 的任意整倍数，要想让它也能度量 a 的话，只须而且必须让它能够度量 c 。于是， y 也就能够同时度量 b 和 c ，根据同样的道理，这又可以推出 y 一定能度量 d ……因此，最后你会发现， y 一定能度量 x 。

    用现在的话来讲，求两条线段的最大公度单位，实际上就是求两个数的最大公约数——最大的能同时整除这两个数的数。用现在的话来描述 Euclid 算法也会简明得多：假设刚开始的两个数是 a 和 b ，其中 a > b ，那么把 a 除以 b 的余数记作 c ，把 b 除以 c 的余数记作 d ，c 除以 d 余 e ， d 除以 e 余 f ，等等等等，不断拿上一步的除数去除以上一步的余数。直到某一次除法余数为 0 了，那么此时的除数就是最终结果。因此， Euclid 算法又有一个形象的名字，叫做“辗转相除法”。

    辗转相除法的效率非常高，刚才大家已经看到了，计算 690 和 2202 的最大公约数时，我们依次得到的余数是 132, 30, 12, 6 ，做第 5 次除法时就除尽了。实际上，我们可以大致估计出辗转相除法的效率。第一次做除法时，我们是用 a 来除以 b ，把余数记作 c 。如果 b 的值不超过 a 的一半，那么 c 更不会超过 a 的一半（因为余数小于除数）；如果 b 的值超过了 a 的一半，那么显然 c 直接就等于 a – b ，同样小于 a 的一半。因此，不管怎样， c 都会小于 a 的一半。下一步轮到 b 除以 c ，根据同样的道理，所得的余数 d 会小于 b 的一半。接下来， e 将小于 c 的一半， f 将小于 d 的一半，等等等等。按照这种速度递减下去的话，即使最开始的数是上百位的大数，不到 1000 次除法就会变成一位数（如果算法没有提前结束的话），交给计算机来执行的话保证秒杀。用专业的说法就是，辗转相除法的运算次数是对数级别的。

    很长一段时间里，古希腊人都认为，任意两条线段都是可以公度的，我们只需要做一遍辗转相除便能把这个公度单位给找出来。事实真的如此吗？辗转相除法有可能失效吗？我们至少能想到一种可能：会不会有两条长度关系非常特殊的线段，让辗转相除永远达不到终止的条件，从而根本不能算出一个“最终结果”？注意，线段的长度不一定（也几乎不可能）恰好是整数或者有限小数，它们往往是一些根本不能用有限的方式精确表示出来的数。考虑到这一点，两条线段不可公度完全是有可能的。

    为了让两条线段辗转相除永远除不尽，我们有一种绝妙的构造思路：让线段 a 和 b 的比值恰好等于线段 b 和 c 的比值。这样，辗转相除一次后，两数的关系又回到了起点。今后每一次辗转相除，余数总会占据除数的某个相同的比例，于是永远不会出现除尽的情况。不妨假设一种最为简单的情况，即 a 最多只能包含一个 b 的长度，此时 c 等于 a – b 。解方程 a / b = b / (a – b) 可以得到 a : b = 1 : (√5 – 1) / 2 ，约等于一个大家非常熟悉的比值 1: 0.618 。于是我们马上得出：成黄金比例的两条线段是不可公度的。

      

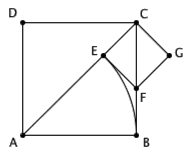
    更典型的例子则是，正方形的边长和对角线是不可公度的。让我们画个图来说明这一点。如图，我们试着用辗转相除求出边长 AB 和对角线 AC 的最大公度单位。按照规则，第一步我们应该用 AB 去度量 AC ，假设所得的零头是 EC 。下一步，我们应该用 EC 去度量 AB ，或者说用 EC 去度量 BC （反正正方形各边都相等）。让我们以 EC 为边作一个小正方形 CEFG ，容易看出 F 点将正好落在 BC 上，同时三角形 AEF 和三角形 ABF 将会由于 HL 全等。因此， EC = EF = BF 。注意到 BC 上已经有一段 BF 和 EC 是相等的了，因而我们用 EC 去度量 BC 所剩的零头，也就相当于用 EC 去度量 FC 所剩的零头。结果又回到了最初的局面——寻找正方形的边长和对角线的公度单位。因而，辗转相除永远不会结束。线段 AB 的长度和线段 AC 的长度不能公度，它们处于两个不同的世界中。

      

    如果正方形 ABCD 的边长 1 ，正方形的面积也就是 1 。从上图中可以看到，若以对角线 AC 为边做一个大正方形，它的面积就该是 2 。因而， AC 就应该是一个与自身相乘之后恰好等于 2 的数，我们通常把这个数记作 √2 。《几何原本》的第十卷专门研究不可公度量，其中就有一段 1 和 √2 不可公度的证明，但所用的方法不是我们上面讲的这种，而更接近于课本上的证明：设 √2 = p / q ，其中 p / q 已是最简分数，但推着推着就发现，这将意味着 p 和 q 都是偶数，与最简分数的假设矛盾。

    用今天的话来讲， 1 和 √2 不可公度，实际上相当于是说 √2 是无理数。因此，古希腊人发现了无理数，这确实当属不争的事实。奇怪的是，无理数的发现常常会几乎毫无根据地归功于一个史料记载严重不足的古希腊数学家 Hippasus 。根据各种不靠谱的描述， Hippasus 的发现触犯了 Pythagoras （古希腊哲学家）的教条，最后被溺死在了海里。

    可公度线段和不可公度线段的概念与有理数和无理数的概念非常接近，我们甚至可以说明这两个概念是等价的——它们之间有一种很巧妙的等价关系。注意到，即使 a 和 b 本身都是无理数， a 和 b 还是有可能被公度的，例如 a = √2 并且 b = 2 · √2 的时候。不过，有一件事我们可以肯定： a 和 b 的比值一定是一个有理数。事实上，可以证明，线段 a 和 b 是可公度的，当且仅当 a / b 是一个有理数。线段 a 和 b 是可公度的，说明存在一个 c 以及两个整数 m 和 n ，使得 a = m · c ，并且 b = n · c 。于是 a / b = (m · c) / (n · c) = m / n ，这是一个有理数。反过来，如果 a / b 是一个有理数，说明存在整数 m 和 n 使得 a / b = m / n ，等式变形后可得 a / m = b / n ，令这个商为 c ，那么 c 就可以作为 a 和 b 的公度单位。

    有时候，“是否可以公度”的说法甚至比“是否有理”更好一些，因为这是一个相对的概念，不是一个绝对的概念。当我们遇到生活当中的某个物理量时，我们绝不能指着它就说“这是一个有理的量”或者“这是一个无理的量”，我们只能说，以某某某（比如 1 厘米、 1 英寸、 0.2 毫米或者一支铅笔的长度等等）作为单位来衡量时，这是一个有理的量或者无理的量。考虑到所选用的单位长度本身也是由另一个物理量定义出来的（比如 1 米被定义为光在真空中 1 秒走过的路程的 1 / 299792458 ），因而在讨论一个物理量是否是有理数时，我们讨论的其实是两个物理量是否可以被公度。

 
（二）中国剩余定理

    如果两个正整数的最大公约数为 1 ，我们就说这两个数是互质的。这是一个非常重要的概念。如果 a 和 b 互质，这就意味着分数 a / b 已经不能再约分了，意味着 a × b 的棋盘的对角线不会经过中间的任何交叉点，意味着循环长度分别为 a 和 b 的两个周期性事件一同上演，则新的循环长度最短为 a · b 。

      

    最后一点可能需要一些解释。让我们来举些例子。假如有 1 路和 2 路两种公交车，其中 1 路车每 6 分钟一班，2 路车每 8 分钟一班。如果你刚刚错过两路公交车同时出发的壮景，那么下一次再遇到这样的事情是多少分钟之后呢？当然， 6 × 8 = 48 分钟，这是一个正确的答案，此时 1 路公交车正好是第 8 班， 2 路公交车正好是第 6 班。不过，实际上，在第 24 分钟就已经出现了两车再次同发的情况了，此时 1 路车正好是第 4 班， 2 路车正好是第 3 班。但是，如果把例子中的 6 分钟和 8 分钟分别改成 4 分钟和 7 分钟，那么要想等到两车再次同发，等到第 4 × 7 = 28 分钟是必须的。类似的，假如某一首歌的长度正好是 6 分钟，另一首歌的长度正好是 8 分钟，让两首歌各自循环播放， 6 × 8 = 48 分钟之后你听到的“合声”将会重复，但实际上第 24 分钟就已经开始重复了。但若两首歌的长度分别是 4 分钟和 7 分钟，则必须到第 4 × 7 = 28 分钟之后才有重复，循环现象不会提前发生。

    究其原因，其实就是，对于任意两个数，两个数的乘积一定是它们的一个公倍数，但若这两个数互质，则它们的乘积一定是它们的最小公倍数。事实上，我们还能证明一个更强的结论： a 和 b 的最大公约数和最小公倍数的乘积，一定等于 a 和 b 的乘积。在第四节中，我们会给出一个证明。

    很多更复杂的数学现象也都跟互质有关。《孙子算经》卷下第二十六问：“今有物，不知其数。三、三数之，剩二；五、五数之，剩三；七、七数之，剩二。问物几何？答曰：二十三。”翻译过来，就是有一堆东西，三个三个数余 2 ，五个五个数余 3 ，七个七个数余 2 ，问这堆东西有多少个？《孙子算经》给出的答案是 23 个。当然，这个问题还有很多其他的解。由于 105 = 3 × 5 × 7 ，因而 105 这个数被 3 除、被 5 除、被 7 除都能除尽。所以，在 23 的基础上额外加上一个 105 ，得到的 128 也是满足要求的解。当然，我们还可以在 23 的基础上加上 2 个 105 ，加上 3 个 105 ，等等，所得的数都满足要求。除了形如 23 + 105n 的数以外，还有别的解吗？没有了。事实上，不管物体总数除以 3 的余数、除以 5 的余数以及除以 7 的余数分别是多少，在 0 到 104 当中总存在唯一解；在这个解的基础上再加上 105 的整倍数后，可以得到其他所有的正整数解。后人将其表述为“中国剩余定理”：给出 m 个两两互质的整数，它们的乘积为 P ；假设有一个未知数 M ，如果我们已知 M 分别除以这 m 个数所得的余数，那么在 0 到 P – 1 的范围内，我们可以唯一地确定这个 M 。这可以看作是 M 的一个特解。其他所有满足要求的 M ，则正好是那些除以 P 之后余数等于这个特解的数。注意，除数互质的条件是必需的，否则结论就不成立了。比如说，在 0 到 7 的范围内，除以 4 余 1 并且除以 2 也余 1 的数有 2 个，除以 4 余 1 并且除以 2 余 0 的数则一个也没有。

    从某种角度来说，中国剩余定理几乎是显然的。让我们以两个除数的情况为例，来说明中国剩余定理背后的直觉吧。假设两个除数分别是 4 和 7 。下表显示的就是各自然数除以 4 和除以 7 的余数情况，其中 x mod y 表示 x 除以 y 的余数，这个记号后面还会用到。

i	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
i mod 4	0	1	2	3	0	1	2	3	0	1	2	3	0	1	2	3	0	1	2	3
i mod 7	0	1	2	3	4	5	6	0	1	2	3	4	5	6	0	1	2	3	4	5
i	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39
i mod 4	0	1	2	3	0	1	2	3	0	1	2	3	0	1	2	3	0	1	2	3
i mod 7	6	0	1	2	3	4	5	6	0	1	2	3	4	5	6	0	1	2	3	4

    i mod 4 的值显然是以 4 为周期在循环， i mod 7 的值显然是以 7 为周期在循环。由于 4 和 7 是互质的，它们的最小公倍数是 4 × 7 = 28 ，因而 (i mod 4, i mod 7) 的循环周期是 28 ，不会更短。因此，当 i 从 0 增加到 27 时， (i mod 4, i mod 7) 的值始终没有出现重复。但是， (i mod 4, i mod 7) 也就只有 4 × 7 = 28 种不同的取值，因而它们正好既无重复又无遗漏地分给了 0 到 27 之间的数。这说明，每个特定的余数组合都在前 28 项中出现过，并且都只出现过一次。在此之后，余数组合将产生长度为 28 的循环，于是每个特定的余数组合都将会以 28 为周期重复出现。这正是中国剩余定理的内容。

    中国剩余定理有很多漂亮的应用，这里我想说一个我最喜欢的。设想这样一个场景：总部打算把一份秘密文件发送给 5 名特工，但直接把文件原封不动地发给每个人，很难保障安全性。万一有特工背叛或者被捕，把秘密泄露给了敌人怎么办？于是就有了电影和小说中经常出现的情节：把绝密文件拆成 5 份， 5 名特工各自只持有文件的 1/5 。不过，原来的问题并没有彻底解决，我们只能祈祷坏人窃取到的并不是最关键的文件片段。因此，更好的做法是对原文件进行加密，每名特工只持有密码的 1/5 ，这 5 名特工需要同时在场才能获取文件全文。但这也有一个隐患：如果真的有特工被抓了，当坏人们发现只拿到其中一份密码没有任何用处的同时，特工们也会因为少一份密码无法解开全文而烦恼。此时，你或许会想，是否有什么办法能够让特工们仍然可以恢复原文，即使一部分特工被抓住了？换句话说，有没有什么密文发布方式，使得只要 5 个人中半数以上的人在场就可以解开绝密文件？这样的话，坏人必须要能操纵半数以上的特工才可能对秘密文件造成实质性的影响。这种秘密共享方式被称为 (3, 5) 门限方案，意即 5 个人中至少 3 人在场才能解开密文。

    利用中国剩余定理，我们可以得到一种巧妙的方案。回想中国剩余定理的内容：给定 m 个两两互质的整数，它们的乘积为 P ；假设有一个未知数 M ，如果我们已知 M 分别除以这 m 个数所得的余数，那么在 0 到 P – 1 的范围内，我们可以唯一地确定这个 M 。我们可以想办法构造这样一种情况， n 个数之中任意 m 个的乘积都比 M 大，但是任意 m – 1 个数的乘积就比 M 小。这样，任意 m 个除数就能唯一地确定 M ，但 m – 1 个数就不足以求出 M 来。 Mignotte 门限方案就用到了这样一个思路。我们选取 n 个两两互质的数，使得最小的 m 个数的乘积比最大的 m – 1 个数的乘积还大。例如，在 (3, 5) 门限方案中，我们可以取 53 、 59 、 64 、 67 、 71 这 5 个数，前面 3 个数乘起来得 200128 ，而后面两个数相乘才得 4757 。我们把文件的密码设为一个 4757 和 200128 之间的整数，比如 123456 。分别算出 123456 除以上面那 5 个数的余数，得到 19 、 28 、 0 、 42 、 58 。然后，把 (53, 19) 、 (59, 28) 、 (64, 0) 、 (67, 42) 、 (71, 58) 分别告诉 5 名特工，也就是说特工 1 只知道密码除以 53 余 19 ，特工 2 只知道密码除以 59 余 28 ，等等。这样，根据中国剩余定理，任意 3 名特工碰头后就可以唯一地确定出 123456 ，但根据 2 名特工手中的信息只能得到成百上千个不定解。例如，假设我们知道了 x 除以 59 余 28 ，也知道了 x 除以 67 余 42 ，那么我们只能确定在 0 和 59 × 67 – 1 之间有一个解 913 ，在 913 的基础上加上 59 × 67 的整倍数，可以得到其他满足要求的 x ，而真正的 M 则可以是其中的任意一个数。

    不过，为了让 Mignotte 门限方案真正可行，我们还需要一种根据余数信息反推出 M 的方法。换句话说，我们需要有一种通用的方法，能够回答《孙子算经》中提出的那个问题。我们会在下一节中讲到。

 
（三）扩展的辗转相除

    中国剩余定理是一个很基本的定理。很多数学现象都可以用中国剩余定理来解释。背九九乘法口诀表时，你或许会发现，写下 3 × 1, 3 × 2, …, 3 × 9 ，它们的个位数正好遍历了 1 到 9 所有的情况。 7 的倍数、 9 的倍数也是如此，但 2 、 4 、 5 、 6 、 8 就不行。 3 、 7 、 9 这三个数究竟有什么特别的地方呢？秘密就在于， 3 、 7 、 9 都是和 10 互质的。比如说 3 ，由于 3 和 10 是互质的，那么根据中国剩余定理，在 0 到 29 之间一定有这样一个数，它除以 3 余 0 ，并且除以 10 余 1 。它将会是 3 的某个整倍数，并且个位为 1 。同样地，在 0 到 29 之间也一定有一个 3 的整倍数，它的个位是 2 ；在 0 到 29 之间也一定有一个 3 的整倍数，它的个位是 3 ……而在 0 到 29 之间，除掉 0 以外， 3 的整倍数正好有 9 个，于是它们的末位就正好既无重复又无遗漏地取遍了 1 到 9 所有的数字。

    这表明，如果 a 和 n 互质，那么 a · x mod n = 1 、 a · x mod n = 2 等所有方程都是有解的。 18 世纪的法国数学家 Étienne Bézout 曾经证明了一个基本上与此等价的定理，这里我们姑且把它叫做“ Bézout 定理”。事实上，我们不但知道上述方程是有解的，还能求出所有满足要求的解来。

    我们不妨花点时间，把方程 a · x mod n = b 和中国剩余定理的关系再理一下。寻找方程 a · x mod n = b 的解，相当于寻找一个 a 的倍数使得它除以 n 余 b ，或者说是寻找一个数 M 同时满足 M mod a = 0 且 M mod n = b 。如果 a 和 n 是互质的，那么根据中国剩余定理，这样的 M 一定存在，并且找到一个这样的 M 之后，在它的基础上加减 a · n 的整倍数，可以得到所有满足要求的 M 。因此，为了解出方程 a · x mod n = b 的所有解，我们也只需要解出方程的某个特解就行了。假如我们找到了方程 a · x mod n = b 中 x 的一个解，在这个解的基础上加上或减去 n 的倍数（相当于在整个被除数 a · x 的基础上加上或者减去 a · n 的倍数，这里的 a · x 就是前面所说的 M ），就能得到所有的解了。

    更妙的是，我们其实只需要考虑形如 a · x mod n = 1 的方程。因为，如果能解出这样的方程， a · x mod n = 2 、 a · x mod n = 3 也都自动地获解了。假如 a · x mod n = 1 有一个解 x = 100 ，由于 100 个 a 除以 n 余 1 ，自然 200 个 a 除以 n 就余 2 ， 300 个 a 除以 n 就余 3 ，等等，等式右边余数不为 1 的方程也都解开了。

    让我们尝试求解 115x mod 367 = 1 。注意，由于 115 和 367 是互质的，因此方程确实有解。我们解方程的基本思路是，不断寻找 115 的某个倍数以及 367 的某个倍数，使得它们之间的差越来越小，直到最终变为 1 。由于 367 除以 115 得 3 ，余 22 ，因而 3 个 115 只比 367 少 22 。于是， 15 个 115 就要比 5 个 367 少 110 ，从而 16 个 115 就会比 5 个 367 多 5 。好了，真正巧妙的就在这里了： 16 个 115 比 5 个 367 多 5 ，但 3 个 115 比 1 个 367 少 22 ，两者结合起来，我们便能找到 115 的某个倍数和 367 的某个倍数，它们只相差 2 ： 16 个 115 比 5 个 367 多 5 ，说明 64 个 115 比 20 个 367 多 20 ，又考虑到 3 个 115 比 1 个 367 少 22 ，于是 67 个 115 只比 21 个 367 少 2 。现在，结合“少 2 ”和“多 5 ”两个式子，我们就能把差距缩小到 1 了： 67 个 115 比 21 个 367 少 2 ，说明 134 个 115 比 42 个 367 少 4 ，而 16 个 115 比 5 个 367 多 5 ，于是 150 个 115 比 47 个 367 多 1 。这样，我们就解出了一个满足 115x mod 367 = 1 的 x ，即 x = 150 。大家会发现，在求解过程，我们相当于对 115 和 367 做了一遍辗转相除：我们不断给出 115 的某个倍数和 367 的某个倍数，通过辗转对比最近的两个结果，让它们的差距从“少 22 ”缩小到“多 5 ”，再到“少 2 ”、“多 1 ”，其中 22, 5, 2, 1 这几个数正是用辗转相除法求 115 和 367 的最大公约数时将会经历的数。因而，算法的步骤数仍然是对数级别的，即使面对上百位上千位的大数，计算机也毫无压力。这种求解方程 a · x mod n = b 的算法就叫做“扩展的辗转相除法”。

    注意，整个算法有时也会以“少 1 ”的形式告终。例如，用此方法求解 128x mod 367 = 1 时，最后会得出 43 个 128 比 15 个 367 少 1 。这下怎么办呢？很简单， 43 个 128 比 15 个 367 少 1 ，但是 367 个 128 显然等于 128 个 367 ，对比两个式子可知， 324 个 128 就会比 113 个 367 多 1 了，于是得到 x = 324 。

    最后还有一个问题：我们最终总能到达“多 1 ”或者“少 1 ”，这正是因为一开始的两个数是互质的。如果方程 a · x mod n = b 当中 a 和 n 不互质，它们的最大公约数是 d > 1 ，那么在 a 和 n 之间做辗转相除时，算到 d 就直接终止了。自然，扩展的辗转相除也将在到达“多 1 ”或者“少 1 ”之前提前结束。那怎么办呢？我们有一种巧妙的处理方法：以 d 为单位重新去度量 a 和 n （或者说让 a 和 n 都除以 d ），问题就变成我们熟悉的情况了。让我们来举个例子吧。假如我们要解方程 24 · x mod 42 = 30 ，为了方便后面的解释，我们来给这个方程编造一个背景：说一盒鸡蛋 24 个，那么买多少盒鸡蛋，才能让所有的鸡蛋 42 个 42 个地数最后正好能余 30 个？我们发现 24 和 42 不是互质的，扩展的辗转相除似乎就没有用了。不过没关系。我们找出 24 和 42 的最大公约数，发现它们的最大公约数是 6 。现在，让 24 和 42 都来除以 6 ，分别得到 4 和 7 。由于 6 已经是 24 和 42 的公约数中最大的了，因此把 24 和 42 当中的 6 除掉后，剩下的 4 和 7 就不再有大于 1 的公约数，从而就是互质的了。好了，现在我们把题目改编一下，把每 6 个鸡蛋视为一个新的单位量，比如说“ 1 把”。记住， 1 把鸡蛋就是 6 个鸡蛋。于是，原问题就变成了，每个盒子能装 4 把鸡蛋，那么买多少盒鸡蛋，才能让所有的鸡蛋 7 把 7 把地数，最后正好会余 5 把？于是，方程就变成了 4 · x mod 7 = 5 。由于此时 4 和 7 是互质的了，因而套用扩展的辗转相除法，此方程一定有解。可以解出特解 x = 3 ，在它的基础上加减 7 的整倍数，可以得到其他所有满足要求的 x 。这就是改编之后的问题的解。但是，虽说我们对原题做了“改编”，题目内容本身却完全没变，连数值都没变，只不过换了一种说法。改编后的题目里需要买 3 盒鸡蛋，改编前的题目里当然也是要买 3 盒鸡蛋。 x = 3 ，以及所有形如 3 + 7n 的数，也都是原方程的解。

    大家或许已经看到了，我们成功地找到了 24 · x mod 42 = 30 的解，依赖于一个巧合： 24 和 42 的最大公约数 6 ，正好也是 30 的约数。因此，改用“把”作单位重新叙述问题，正好最后的“余 30 个”变成了“余 5 把”，依旧是一个整数。如果原方程是 24 · x mod 42 = 31 的话，我们就没有那么走运了，问题将变成“买多少盒才能让最后数完余 5 又 1/6 把”。这怎么可能呢？我们是整把整把地买，整把整把地数，当然余数也是整把整把的。因此，方程 24 · x mod 42 = 31 显然无解。

    综上所述，如果关于 x 的方程 a · x mod n = b 当中的 a 和 n 不互质，那么求出 a 和 n 的最大公约数 d 。如果 b 恰好是 d 的整倍数，那么把方程中的 a 、 n 、 b 全都除以 d ，新的 a 和 n 就互质了，新的 b 也恰好为整数，用扩展的辗转相除求解新方程，得到的解也就是原方程的解。但若 b 不是 d 的整倍数，则方程无解。

    扩展的辗转相除法有很多应用，其中一个有趣的应用就是大家小时候肯定见过的“倒水问题”。假如你有一个 3 升的容器和一个 5 升的容器（以及充足的水源），如何精确地取出 4 升的水来？为了叙述简便，我们不妨把 3 升的容器和 5 升的容器分别记作容器 A 和容器 B 。一种解法如下：

      1. 将 A 装满，此时 A 中的水为 3 升， B 中的水为 0 升；
      2. 将 A 里的水全部倒入 B ，此时 A 中的水为 0 升， B 中的水为 3 升；
      3. 将 A 装满，此时 A 中的水为 3 升， B 中的水为 3 升；
      4. 将 A 里的水倒入 B 直到把 B 装满，此时 A 中的水为 1 升， B 中的水为 5 升；
      5. 将 B 里的水全部倒掉，此时 A 中的水为 1 升， B 中的水为 0 升；
      6. 将 A 里剩余的水全部倒入 B ，此时 A 中的水为 0 升， B 中的水为 1 升；
      7. 将 A 装满，此时 A 中的水为 3 升， B 中的水为 1 升；
      8. 将 A 里的水全部倒入 B ，此时 A 中的水为 0 升， B 中的水为 4 升；

    这样，我们就得到 4 升的水了。显然，这类问题可以编出无穷多个来，比如能否用 7 升的水杯和 13 升的水杯量出 5 升的水，能否又用 9 升的水杯和 15 升的水杯量出 10 升的水，等等。这样的问题有什么万能解法吗？有！注意到，前面用 3 升的水杯和 5 升的水杯量出 4 升的水，看似复杂的步骤可以简单地概括为：不断将整杯整杯的 A 往 B 里倒，期间只要 B 被装满就把 B 倒空。由于 3 × 3 mod 5 = 4 ，因而把 3 杯的 A 全部倒进 B 里，并且每装满一个 B 就把水倒掉， B 里面正好会剩下 4 升的水。类似地，用容积分别为 a 和 b 的水杯量出体积为 c 的水，实际上相当于解方程 a · x mod b = c 。如果 c 是 a 和 b 的最大公约数，或者能被它们的最大公约数整除，用扩展的辗转相除便能求出 x ，得到对应的量水方案。特别地，如果两个水杯的容积互质，问题将保证有解。如果 c 不能被 a 和 b 的最大公约数整除，方程就没有解了，怎么办？不用着急，因为很显然，此时问题正好也没有解。比方说 9 和 15 都是 3 的倍数，那我们就把每 3 升的水视作一个单位，于是你会发现，在 9 升和 15 升之间加加减减，倒来倒去，得到的量永远只能在 3 的倍数当中转，绝不可能弄出 10 升的水来。这样一来，我们就给出了问题有解无解的判断方法，以及在有解时生成一种合法解的方法，从而完美地解决了倒水问题。

    最后，让我们把上一节留下的一点悬念给补完：怎样求解《孙子算经》中的“今有物，不知其数”一题。已知有一堆东西，三个三个数余 2 ，五个五个数余 3 ，七个七个数余 2 ，问这堆东西有多少个？根据中国剩余定理，由于除数 3 、 5 、 7 两两互质，因而在 0 到 104 之间，该问题有唯一的答案。我们求解的基本思路就是，依次找出满足每个条件，但是又不会破坏掉其他条件的数。我们首先要寻找一个数，它既是 5 的倍数，又是 7 的倍数，同时除以 3 正好余 2 。这相当于是在问， 35 的多少倍除以 3 将会余 2 。于是，我们利用扩展的辗转相除法求解方程 35x mod 3 = 2 。这个方程是一定有解的，因为 5 和 3 、 7 和 3 都是互质的，从而 5 × 7 和 3 也是互质的（到了下一节，这一点会变得很显然）。解这个方程可得 x = 1 。于是， 35 就是我们要找到的数。第二步，是寻找这么一个数，它既是 3 的倍数，又是 7 的倍数，同时除以 5 余 3 。这相当于求解方程 21x mod 5 = 3 ，根据和刚才相同的道理，这个方程一定有解。可以解得 x = 3 ，因此我们要找的数就是 63 。最后，我们需要寻找一个数，它能同时被 3 和 5 整除，但被 7 除余 2 。这相当于求解方程 15x mod 7 = 2 ，解得 x = 2 。我们想要找的数就是 30 。现在，如果我们把 35 、 63 和 30 这三个数加在一起会怎么样？它将会同时满足题目当中的三个条件！它满足“三个三个数余 2 ”，因为 35 除以 3 是余 2 的，而后面两个数都是 3 的整倍数，所以加在一起后除以 3 仍然余 2 。类似地，它满足“五个五个数余 3 ”，因为 63 除以 5 余 3 ，另外两个数都是 5 的倍数。类似地，它也满足“七个七个数余 2 ”，因而它就是原问题的一个解。你可以验证一下， 35 + 63 + 30 = 128 ，它确实满足题目的所有要求！为了得出一个 0 到 104 之间的解，我们在 128 的基础上减去一个 105 ，于是正好得到《孙子算经》当中给出的答案， 23 。

    已知 M 除以 m 个两两互质的数之后所得的余数，利用类似的方法总能反解出 M 来。至此，我们也就完成了 Mignotte 秘密共享方案的最后一环。

 
（四）Fermat 小定理

    很多自然数都可以被分解成一些更小的数的乘积，例如 12 可以被分成 4 乘以 3 ，其中 4 还可以继续地被分成 2 乘以 2 ，因而我们可以把 12 写作 2 × 2 × 3 。此时， 2 和 3 都不能再继续分解了，它们是最基本、最纯净的数。我们就把这样的数叫做“质数”或者“素数”。同样地， 2 、 3 、 5 、 7 、 11 、 13 等等都是不可分解的，它们也都是质数。它们是自然数的构件，是自然数世界的基本元素。 12 是由两个 2 和一个 3 组成的，正如水分子是由两个氢原子和一个氧原子组成的一样。只不过，和化学世界不同的是，自然数世界里的基本元素是无限的——质数有无穷多个。

    关于为什么质数有无穷多个，古希腊的 Euclid 有一个非常漂亮的证明。假设质数只有有限个，其中最大的那个质数为 p 。现在，把所有的质数全部乘起来，再加上 1 ，得到一个新的数 N 。也就是说， N 等于 2 · 3 · 5 · 7 · … · p + 1 。注意到， N 除以每一个质数都会余 1 ，比如 N 除以 2 就会商 3 · 5 · 7 · … · p 余 1 ， N 除以 3 就会商 2 · 5 · 7 · … · p 余 1 ，等等。这意味着， N 不能被任何一个质数整除，换句话说 N 是不能被分解的，它本身就是质数。然而这也不对，因为 p 已经是最大的质数了，于是产生了矛盾。这说明，我们刚开始的假设是错的，质数应该有无穷多个。需要额外说明的一点是，这个证明容易让人产生一个误解，即把头 n 个质数乘起来再加 1 ，总能产生一个新的质数。这是不对的，因为既然我们无法把全部质数都乘起来，那么所得的数就有可能是由那些我们没有乘进去的质数构成的，比如 2 · 3 · 5 · 7 · 11 · 13 + 1 = 30031 ，它可以被分解成 59 × 509 。

    从古希腊时代开始，人们就近乎疯狂地想要认识自然数的本质规律。组成自然数的基本元素自然地就成为了一个绝佳的突破口，于是对质数的研究成为了探索自然数世界的一个永久的话题。这就是我们今天所说的“数论”。

    用质数理论来研究数，真的会非常方便。 a 是 b 的倍数（或者说 a 能被 b 整除， b 是 a 的约数），意思就是 a 拥有 b 所含的每一种质数，而且个数不会更少。我们举个例子吧，比如说 b = 12 ，它可以被分解成 2 × 2 × 3 ， a = 180 ，可以被分解成 2 × 2 × 3 × 3 × 5 。 b 里面有两个 2 ，这不稀罕， a 里面也有两个 2 ； b 里面有一个 3 ，这也没什么， a 里面有两个 3 呢。况且， a 里面还包含有 b 没有的质数， 5 。对于每一种质数， b 里面所含的个数都比不过 a ，这其实就表明了 b 就是 a 的约数。

    现在，假设 a = 36 = 2 × 2 × 3 × 3 ， b = 120 = 2 × 2 × 2 × 3 × 5 。那么， a 和 b 的最大公约数是多少？我们可以依次考察，最大公约数里面可以包含哪些质数，每个质数都能有多少个。这个最大公约数最多可以包含多少个质数 2 ？显然最多只能包含两个，否则它就不能整除 a 了；这个最大公约数最多可以包含多少个质数 3 ？显然最多只能包含一个，否则它就不能整除 b 了；这个最大公约数最多可以包含多少个质数 5 ？显然一个都不能有，否则它就不能整除 a 了。因此， a 和 b 的最大公约数就是 2 × 2 × 3 = 12 。

    在构造 a 和 b 的最小公倍数时，我们希望每种质数在数量足够的前提下越少越好。为了让这个数既是 a 的倍数，又是 b 的倍数，三个 2 是必需的；为了让这个数既是 a 的倍数，又是 b 的倍数，两个 3 是必需的；为了让这个数既是 a 的倍数，又是 b 的倍数，那一个 5 也是必不可少的。因此， a 和 b 的最小公倍数就是 2 × 2 × 2 × 3 × 3 × 5 = 360 。

    你会发现， 12 × 360 = 36 × 120 ，最大公约数乘以最小公倍数正好等于原来两数的乘积。这其实并不奇怪。在最大公约数里面，每种质数各有多少个，取决于 a 和 b 当中谁所含的这种质数更少一些。在最小公倍数里面，每种质数各有多少个，取决于 a 和 b 当中谁所含的这种质数更多一些。因此，对于每一种质数而言，最大公约数和最小公倍数里面一共包含了多少个这种质数， a 和 b 里面也就一共包含了多少个这种质数。最大公约数和最小公倍数乘在一起，也就相当于是把 a 和 b 各自所包含的质数都乘了个遍，自然也就等于 a 与 b 的乘积了。这立即带来了我们熟悉的推论：如果两数互质，这两数的乘积就是它们的最小公倍数。

    第三节里，我们曾说到，“因为 5 和 3 、 7 和 3 都是互质的，从而 5 × 7 和 3 也是互质的”。利用质数的观点，这很容易解释。两个数互质，相当于是说这两个数不包含任何相同的质数。如果 a 与 c 互质， b 与 c 互质，显然 a · b 也与 c 互质。另外一个值得注意的结论是，如果 a 和 b 是两个不同的质数，则这两个数显然就直接互质了。事实上，只要知道了 a 是质数，并且 a 不能整除 b ，那么不管 b 是不是质数，我们也都能确定 a 和 b 是互质的。我们后面会用到这些结论。

    在很多场合中，质数都扮演着重要的角色。 1640 年，法国业余数学家 Pierre de Fermat （通常译作“费马”）发现，如果 n 是一个质数的话，那么对于任意一个数 a ， a 的 n 次方减去 a 之后都将是 n 的倍数。例如， 7 是一个质数，于是 2⁷ – 2 、 3⁷ – 3 ， 4⁷ – 4 ，甚至 100⁷ – 100 ，统统都能被 7 整除。但 15 不是质数（它可以被分解为 3 × 5 ），于是 a¹⁵ – a 除以 15 之后就可能会出现五花八门的余数了。这个规律在数论研究中是如此基本如此重要，以至于它有一个专门的名字—— Fermat 小定理。作为一个业余数学家， Fermat 发现了很多数论中精彩的结论， Fermat “小”定理只是其中之一。虽然与本文无关，但有一点不得不提：以 Fermat 的名字命名的东西里，最著名的要数 Fermat 大定理了（其实译作“ Fermat 最终定理”更贴切）。如果你没听说过，上网查查，或者看看相关的书籍。千万不要错过与此相关的一系列激动人心的故事。

    言归正传。 Fermat 小定理有一个非常精彩的证明。我们不妨以“ 3⁷ – 3 能被 7 整除”为例进行说明，稍后你会发现，对于其他的情况，道理是一样的。首先，让我来解释一下“循环移位”的意思。想象一个由若干字符所组成的字符串，在一块大小刚好合适的 LED 屏幕上滚动显示。比方说， HELLOWORLD 就是一个 10 位的字符串，而我们的 LED 屏幕不多不少正好容纳 10 个字符。刚开始，屏幕上显示 HELLOWORLD 。下一刻，屏幕上的字母 H 将会移出屏幕，但又会从屏幕右边移进来，于是屏幕变成了 ELLOWORLDH 。下一刻，屏幕变成了 LLOWORLDHE ，再下一刻又变成了 LOWORLDHEL 。移动到第 10 次，屏幕又会回到 HELLOWORLD 。在此过程中，屏幕上曾经显示过的 ELLOWORLDH, LLOWORLDHE, LOWORLDHEL, … ，都是由初始的字符串 HELLOWORLD 通过“循环移位”得来的。现在，考虑所有仅由 A 、 B 、 C 三个字符组成的长度为 7 的字符串，它们一共有 3⁷ 个。如果某个字符串循环移位后可以得到另一个字符串，我们就认为这两个字符串属于同一组字符串。比如说， ABBCCCC 和 CCCABBC 就属于同一组字符串，并且该组内还有其他 5 个字符串。于是，在所有 3⁷ 个字符串当中，除了 AAAAAAA 、 BBBBBBB 、 CCCCCCC 这三个特殊的字符串以外，其他所有的字符串正好都是每 7 个一组。这说明， 3⁷ – 3 能被 7 整除。

    在这个证明过程中，“ 7 是质数”这个条件用到哪里去了？仔细想想你会发现，正因为 7 是质数，所以每一组里才恰好有 7 个字符串。如果字符串的长度不是 7 而是 15 的话，有些组里将会只含 3 个或者 5 个字符串。比方说， ABCABCABCABCABC 所在的组里就只有 3 个字符串，循环移动 3 个字符后，字符串将会和原来重合。

    Fermat 小定理有一个等价的表述：如果 n 是一个质数的话，那么对于任意一个数 a ，随着 i 的增加， a 的 i 次方除以 n 的余数将会呈现出长度为 n – 1 的周期性（下表所示的是 a = 3 、 n = 7 的情况）。这是因为，根据前面的结论， aⁿ 与 a 的差能够被 n 整除，这说明 aⁿ 和 a 分别都除以 n 之后将会拥有相同的余数。这表明，依次计算 a 的 1 次方、 2 次方、 3 次方除以 n 的余数，算到 a 的 n 次方时，余数将会变得和最开始相同。另一方面， aⁱ 除以 n 的余数，完全由 a^i-1 除以 n 的余数决定。比方说，假如我们已经知道 3³ 除以 7 等于 3 余 6 ，这表明 3³ 里包含 3 个 7 以及 1 个 6 ；因此， 3⁴ 里就包含 9 个 7 以及 3 个 6 ，或者说 9 个 7 以及 1 个 18 。为了得到 3⁴ 除以 7 的余数，只需要看看 18 除以 7 余多少就行了。可见，要想算出 a^i-1 · a 除以 n 的余数，我们不需要完整地知道 a^i-1 的值，只需要知道 a^i-1 除以 n 的余数就可以了。反正最后都要对乘积取余，相乘之前事先对乘数取余不会对结果造成影响（记住这一点，后面我们还会多次用到）。既然第 n 个余数和第 1 个余数相同，而余数序列的每一项都由上一项决定，那么第 n + 1 个、第 n + 2 个余数也都会跟着和第 2 个、第 3 个余数相同，余数序列从此处开始重复，形成长为 n – 1 的周期。

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
3i	3	9	27	81	243	729	2187	6561	19683	59049	177147	531441	1594323	4782969	14348907
3i mod 7	3	2	6	4	5	1	3	2	6	4	5	1	3	2	6

    需要注意的是， n – 1 并不见得是最小的周期。下表所示的是 2ⁱ 除以 7 的余数情况，余数序列确实存在长度为 6 的周期现象，但实际上它有一个更小的周期， 3 。

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
2i	2	4	8	16	32	64	128	256	512	1024	2048	4096	8192	16384	32768
2i mod 7	2	4	1	2	4	1	2	4	1	2	4	1	2	4	1

    那么，如果除数 n 不是质数，而是两个质数的乘积（比如 35 ），周期的长度又会怎样呢？让我们试着看看， 3ⁱ 除以 35 的余数有什么规律吧。注意到 5 和 7 是两个不同的质数，因而它们是互质的。根据中国剩余定理，一个数除以 35 的余数就可以唯一地由它除以 5 的余数和除以 7 的余数确定出来。因而，为了研究 3ⁱ 除以 35 的余数，我们只需要观察 (3ⁱ mod 5, 3ⁱ mod 7) 即可。由 Fermat 小定理可知，数列 3ⁱ mod 5 有一个长为 4 的周期，数列 3ⁱ mod 7 有一个长为 6 的周期。 4 和 6 的最小公倍数是 12 ，因此 (3ⁱ mod 5, 3ⁱ mod 7) 存在一个长为 12 的周期。到了 i = 13 时， (3ⁱ mod 5, 3ⁱ mod 7) 将会和最开始重复，于是 3ⁱ 除以 35 的余数将从此处开始发生循环。

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22
3i mod 5	3	4	2	1	3	4	2	1	3	4	2	1	3	4	2	1	3	4	2	1	3	4
3i mod 7	3	2	6	4	5	1	3	2	6	4	5	1	3	2	6	4	5	1	3	2	6	4
3i mod 35	3	9	27	11	33	29	17	16	13	4	12	1	3	9	27	11	33	29	17	16	13	4
i	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44
3i mod 5	2	1	3	4	2	1	3	4	2	1	3	4	2	1	3	4	2	1	3	4	2	1
3i mod 7	5	1	3	2	6	4	5	1	3	2	6	4	5	1	3	2	6	4	5	1	3	2
3i mod 35	12	1	3	9	27	11	33	29	17	16	13	4	12	1	3	9	27	11	33	29	17	16

    类似地，假如某个整数 n 等于两个质数 p 、 q 的乘积，那么对于任意一个整数 a ，写出 aⁱ 依次除以 n 所得的余数序列， p – 1 和 q – 1 的最小公倍数将成为该序列的一个周期。事实上， p – 1 和 q – 1 的任意一个公倍数，比如表达起来最方便的 (p – 1) × (q – 1) ，也将成为该序列的一个周期。这个规律可以用来解释很多数学现象。例如，大家可能早就注意过，任何一个数的乘方，其个位数都会呈现长度为 4 的周期（这包括了周期为 1 和周期为 2 的情况）。其实这就是因为， 10 等于 2 和 5 这两个质数的乘积，而 (2 – 1) × (5 – 1) = 4，因此任意一个数的乘方除以 10 的余数序列都将会产生长为 4 的周期。

i	1	2	3	4	5	6	7	8	9	10
3i	3	9	27	81	243	729	2187	6561	19683	59049
3i的个位	3	9	7	1	3	9	7	1	3	9
4i	4	16	64	256	1024	4096	16384	65536	262144	1048576
4i的个位	4	6	4	6	4	6	4	6	4	6
5i	5	25	125	625	3125	15625	78125	390625	1953125	9765625
5i的个位	5	5	5	5	5	5	5	5	5	5

    1736 年，瑞士大数学家 Leonhard Euler （通常译作“欧拉”）对此做过进一步研究，讨论了当 n 是更复杂的数时推导余数序列循环周期的方法，得到了一个非常漂亮的结果：在 1 到 n 的范围内有多少个数和 n 互质（包括 1 在内）， a 的 i 次方除以 n 的余数序列就会有一个多长的周期。这个经典的结论就叫做“ Euler 定理”。作为历史上最高产的数学家之一， Euler 的一生当中发现的定理实在是太多了。为了把上述定理和其他的“ Euler 定理”区别开来，有时也称它为“ Fermat – Euler 定理”。这是一个非常深刻的定理，它有一些非常具有启发性的证明方法。考虑到在后文的讲解中这个定理不是必需的，因此这里就不详说了。

    这些东西有什么用呢？没有什么用。几千年来，数论一直没有任何实际应用，数学家们研究数论的动力完全来源于数字本身的魅力。不过，到了 1970 年左右，情况有了戏剧性的变化。

    有的朋友可能要说了，你怎么赖皮呢，“没有任何实际应用”，那刚才的 Mignotte 秘密共享方案算什么？其实， Mignotte 秘密共享方案已经是很后来的事了。秘密共享本来远没那么复杂，为了使得只要 5 个人中半数以上的人在场就可以解开绝密文件，总部可以把绝密文件锁进一个特殊的机械装置里，装置上有三个一模一样的锁孔，并配有 5 把完全相同且不可复制的钥匙。只有把其中任意 3 把钥匙同时插进钥匙孔并一起转动，才能打开整个装置。把 5 把钥匙分发给 5 名特工，目的就直接达到了。因而，通常情况下我们并不需要动用 Mignotte 秘密共享方案。那么，利用中国剩余定理费尽周折弄出的 Mignotte 秘密共享方案，意义究竟何在呢？这种新的秘密共享方案直到 1983 年才被提出，想必是为了解决某个以前不曾有过的需求。 20 世纪中后期究竟出现了什么？答案便是——计算机网络。锁孔方案只适用于物理世界，不能用于网络世界。为了在网络世界中共享秘密，我们需要一种纯信息层面的、只涉及数据交换的新方法， Mignotte 秘密共享方案才应运而生。

    数论知识开始焕发新生，一切都是因为这该死的计算机网络。

 
（五）公钥加密的可能性

    计算机网络的出现无疑降低了交流的成本，但却给信息安全带来了难题。在计算机网络中，一切都是数据，一切都是数字，一切都是透明的。假如你的朋友要给你发送一份绝密文件，你如何阻止第三者在你们的通信线路的中间节点上窃走信息？其中一种方法就是，让他对发送的数据进行加密，密码只有你们两人知道。但是，这个密码又是怎么商定出来的呢？直接叫对方编好密码发给你的话，密码本身会有泄漏的风险；如果让对方给密码加个密再发过来呢，给密码加密的方式仍然不知道该怎么确定。如果是朋友之间的通信，把两人已知的小秘密用作密钥（例如约定密钥为 A 的生日加上 B 的手机号）或许能让人放心许多；但对于很多更常见的情形，比方说用户在邮件服务提供商首次申请邮箱时，会话双方完全没有任何可以利用的公共秘密。此时，我们需要一个绝对邪的办法……如果说我不告诉任何人解密的算法呢？这样的话，我就可以公开加密的方法，任何人都能够按照这种方法对信息进行加密，但是只有我自己才知道怎样给由此得到的密文解密。然后，让对方用这种方法给文件加密传过来，问题不就解决了吗？这听上去似乎不太可能，因为直觉上，知道加密的方法也就知道了解密的方法，只需要把过程反过来做就行了。加密算法和解密算法有可能是不对称的吗？

    有可能。小时候我经常在朋友之间表演这么一个数学小魔术：让对方任意想一个三位数，把这个三位数乘以 91 的乘积的末三位告诉我，我便能猜出对方原来想的数是多少。如果对方心里想的数是 123 ，那么对方就计算出 123 × 91 等于 11193 ，并把结果的末三位 193 告诉我。看起来，这么做似乎损失了不少信息，让我没法反推出原来的数。不过，我仍然有办法：只需要把对方告诉我的结果再乘以 11 ，乘积的末三位就是对方刚开始想的数了。你可以验证一下， 193 × 11 = 2123 ，末三位正是对方所想的秘密数字！其实道理很简单， 91 乘以 11 等于 1001 ，而任何一个三位数乘以 1001 后，末三位显然都不变（例如 123 乘以 1001 就等于 123123 ）。先让对方在他所想的数上乘以 91 ，假设乘积为 X ；我再在 X 的基础上乘以 11 ，其结果相当于我俩合作把原数乘以了 1001 ，自然末三位又变了回去。然而， X 乘以 11 后的末三位是什么，只与 X 的末三位有关。因此，对方只需要告诉我 X 的末三位就行了，这并不会丢掉信息。站在数论的角度来看，上面这句话有一个更好的解释：反正最后都要取除以 1000 的余数，在中途取一次余数不会有影响（还记得吗，“反正最后都要对乘积取余，相乘之前事先对乘数取余不会对结果造成影响”）。知道原理后，我们可以构造一个定义域和值域更大的加密解密系统。比方说，任意一个数乘以 500000001 后，末 8 位都不变，而 500000001 = 42269 × 11829 ，于是你来乘以 42269 ，我来乘以 11829 ，又一个加密解密不对称的系统就构造好了。这是一件很酷的事情，任何人都可以按照我的方法加密一个数，但是只有我才知道怎么把所得的密文变回去。在现代密码学中，数论渐渐地开始有了自己的地位。

    不过，加密和解密的过程不对称，并不妨碍我们根据加密方法推出解密方法来，虽然这可能得费些功夫。比方说，刚才的加密算法就能被破解：猜出对方心里想的数相当于求解形如 91x mod 1000 = 193 的方程，这可以利用扩展的辗转相除法很快求解出来，根本不需要其他的雕虫小技（注意到 91 和 1000 是互质的，根据 Bézout 定理，方程确实保证有解）。为了得到一个可以公开加密钥匙的算法，我们还需要从理论上说服自己，在只知道加密钥匙的情况下构造出解密钥匙是非常非常困难的。

    1970 年左右，科学家们开始认真地思考“公钥加密系统”的可能性。 1977 年，来自 MIT 的 Ron Rivest 、 Adi Shamir 和 Leonard Adleman 三个人合写了一篇论文，给出了一种至今仍然安全的公钥加密算法。随后，该算法以三人名字的首字母命名，即 RSA 算法。

    RSA 算法为什么会更加安全呢？因为 RSA 算法用到了一种非常犀利的不对称性——大数分解难题。

    为了判断一个数是不是质数，最笨的方法就是试除法——看它能不能被 2 整除，如果不能的话再看它能不能被 3 整除，这样不断试除上去。直到除遍了所有比它小的数，都还不能把它分解开来，它就是质数了。但是，试除法的速度太慢了，我们需要一些高效的方法。 Fermat 素性测试就是一种比较常用的高效方法，它基于如下原理： Fermat 小定理对一切质数都成立。回想 Fermat 小定理的内容：如果 n 是一个质数的话，那么对于任意一个数 a ， a 的 n 次方减去 a 之后都将是 n 的倍数。为了判断 209 是不是质数，我们随便选取一个 a ，比如 38 。结果发现，38²⁰⁹ – 38 除以 209 余 114 （稍后我们会看到，即使把 209 换成上百位的大数，利用计算机也能很快算出这个余数来），不能被 209 整除。于是， 209 肯定不是质数。我们再举一个例子。为了判断 221 是不是质数，我们随机选择 a ，比如说还是 38 吧。你会发现 38²²¹ – 38 除以 221 正好除尽。那么， 221 是否就一定是质数了呢？麻烦就麻烦在这里：这并不能告诉我们 221 是质数，因为 Fermat 小定理毕竟只说了对一切质数都成立，但没说对其他的数成不成立。万一 221 根本就不是质数，但 a = 38 时碰巧也符合 Fermat 小定理呢？为了保险起见，我们不妨再选一个不同的 a 值。比方说，令 a = 26 ，可以算出 26²²¹ – 26 除以 221 余 169 ，因而 221 果然并不是质数。这个例子告诉了我们，如果运气不好的话，所选的 a 值会让不是质数的数也能骗过检测，虽然这个概率其实并不大。因此，我们通常的做法便是，多选几个不同的 a ，只要有一次没通过测试，被检测的数一定不是质数，如果都通过测试了，则被检测的数很可能是质数。没错， Fermat 素性测试的效率非常高，但它是基于一定概率的，有误报的可能。如果发现某个数 n 不满足 Fermat 小定理，它一定不是质数；但如果发现某个数 n 总能通过 Fermat 小定理的检验，只能说明它有很大的几率是质数。

    Fermat 素性测试真正麻烦的地方就是，居然有这么一种极其特殊的数，它不是质数，但对于任意的 a 值，它都能通过测试。这样的数叫做 Carmichael 数，最小的一个是 561 ，接下来的几个则是 1105, 1729, 2465, 2821, 6601, 8911… 虽然不多，但很致命。因此，在实际应用时，我们通常会选用 Miller-Rabin 素性测试算法。这个算法以 Gary Miller 的研究成果为基础，由 Michael Rabin 提出，时间大约是 1975 年。它可以看作是对 Fermat 素性测试的改良。如果选用了 k 个不同的 a 值，那么 Miller-Rabin 素性测试算法出现误判的概率不会超过 1 / 4^k ，足以应付很多现实需要了。

    有没有什么高效率的、确定性的质数判定算法呢？有，不过这已经是很后来的事情了。 2002 年， Manindra Agrawal 、 Neeraj Kayal 和 Nitin Saxena 发表了一篇重要的论文 PRIMES is in P ，给出了第一个高效判断质数的确定性算法，并以三人名字的首字母命名，叫做 AKS 素性测试。不过，已有的质数判断算法已经做得很好了，因此对于 AKS 来说，更重要的是它的理论意义。

    有了判断质数的算法，要想生成一个很大的质数也并不困难了。一种常见的做法是，先选定一串连续的大数，然后去掉其中所有能被 2 整除的数，再去掉所有能被 3 整除的数，再去掉所有能被 5 整除的数……直到把某个范围内（比如说 65000 以内）的所有质数的倍数全都去掉。剩下的数就不多了，利用判断质数的算法对它们一一进行测试，不久便能找出一个质数来。

    怪就怪在，我们可以高效地判断一个数是不是质数，我们可以高效地生成一个很大的质数，但我们却始终找不到高效的大数分解方法。任意选两个比较大的质数，比如 19394489 和 27687937 。我们能够很容易计算出 19394489 乘以 27687937 的结果，它等于 536993389579193 ；但是，除了试除法以外，目前还没有什么本质上更有效的方法（也很难找到更有效的方法）能够把 536993389579193 迅速分解成 19394489 乘以 27687937 。这种不对称性很快便成了现代密码学的重要基础。让我们通过一个有趣的例子来看看，大数分解的困难性是如何派上用场的吧。

    假如你和朋友用短信吵架，最后决定抛掷硬币来分胜负，正面表示你获胜，反面表示对方获胜。问题来了——两个人如何通过短信公平地抛掷一枚硬币？你可以让对方真的抛掷一枚硬币，然后将结果告诉你，不过前提是，你必须充分信任对方才行。在双方互不信任的情况下，还有办法模拟一枚虚拟硬币吗？在我们生活中，有一个常见的解决方法：考你一道题，比如“明天是否会下雨”、“地球的半径是多少”或者“《新华字典》第 307 页的第一个字是什么”，猜对了就算你赢，猜错了就算你输。不过，上面提到的几个问题显然都不是完全公平的。我们需要一类能快速生成的、很难出现重复的、解答不具技巧性的、猜对猜错几率均等的、具有一个确凿的答案并且知道答案后很容易验证答案正确性的问题。大数分解为我们构造难题提供了一个模板。比方说，让对方选择两个 90 位的大质数，或者三个 60 位的大质数，然后把乘积告诉你。无论是哪种情况，你都会得到一个大约有 180 位的数。你需要猜测这个数究竟是两个质数乘在一起得来的，还是三个质数乘在一起得来的。猜对了就算正面，你赢；猜错了就算反面，对方赢。宣布你的猜测后，让对方公开他原先想的那两个数或者三个数，由你来检查它们是否确实都是质数，乘起来是否等于之前给你的数。

    大数分解难题成为了 RSA 算法的理论基础。

 
（六）RSA 算法

    所有工作都准备就绪，下面我们可以开始描述 RSA 算法了。

    首先，找两个质数，比如说 13 和 17 。实际使用时，我们会选取大得多的质数。把它们乘在一起，得 221 。再计算出 (13 – 1) × (17 – 1) = 192。根据前面的结论，任选一个数 a ，它的 i 次方除以 221 的余数将会呈现长度为 192 的周期（虽然可能存在更短的周期）。换句话说，对于任意的一个 a，a, a¹⁹³, a³⁸⁵, a⁵⁷⁷, … 除以 221 都拥有相同的余数。注意到， 385 可以写成 11 × 35 ……嘿嘿，这下我们就又能变数学小魔术了。叫一个人随便想一个不超过 221 的数，比如 123 。算出 123 的 11 次方除以 221 的余数，把结果告诉你。如果他的计算是正确的，你将会得到 115 这个数。看上去，我们似乎很难把 115 还原回去，但实际上，你只需要计算 115 的 35 次方，它除以 221 的余数就会变回 123 。这是因为，对方把他所想的数 123 连乘了 11 次，得到了一个数 X ；你再把这个 X 乘以自身 35 次，这相当于你们合作把 123 连乘了 385 次，根据周期性现象，它除以 221 的余数仍然是 123 。然而，计算 35 个 X 连乘时，反正我们要取乘积除以 221 的余数，因此我们不必完整地获知 X 的值，只需要知道 X 除以 221 的余数就够了。因而，让对方只告诉你 X 取余后的结果，不会造成信息的丢失。

    不过这一次，只知道加密方法后，构造解密方法就难了。容易看出， 35 之所以能作为解密的钥匙，是因为 11 乘以 35 的结果在数列 193, 385, 577, … 当中，它除以 192 的余数正好是 1 。因此，攻击者可以求解 11x mod 192 = 1 ，找出满足要求的密钥 x 。但关键是，他怎么知道 192 这个数？要想得到 192 这个数，我们需要把 221 分解成 13 和 17 的乘积。当最初所选的质数非常非常大时，这一点是很难办到的。

    根据这个原理，我们可以选择两个充分大的质数 p 和 q ，并算出 n = p · q 。接下来，算出 m = (p – 1)(q – 1) 。最后，找出两个数 e 和 d ，使得 e 乘以 d 的结果除以 m 余 1 。怎么找到这样的一对 e 和 d 呢？很简单。首先，随便找一个和 m 互质的数（这是可以做到的，比方说，可以不断生成小于 m 的质数，直到找到一个不能整除 m 的为止），把它用作我们的 e 。然后，求解关于 d 的方程 e · d mod m = 1（就像刚才攻击者想要做的那样，只不过我们有 m 的值而他没有）。 Bézout 定理将保证这样的 d 一定存在。

    好了，现在， e 和 n 就可以作为加密钥匙公之于众， d 和 n 则是只有自己知道的解密钥匙。因而，加密钥匙有时也被称作公钥，解密钥匙有时也被称作私钥。任何知道公钥的人都可以利用公式 c = a^e mod n 把原始数据 a 加密成一个新的数 c ；私钥的持有者则可以计算 c^d mod n ，恢复出原始数据 a 来。不过这里还有个大问题： e 和 d 都是上百位的大数，怎么才能算出一个数的 e 次方或者一个数的 d 次方呢？显然不能老老实实地算那么多次乘法，不然效率实在太低了。好在，“反复平方”可以帮我们快速计算出一个数的乘方。比方说，计算 a³⁵ 相当于计算 a³⁴ · a ，也即 (a¹⁷)² · a ，也即 (a¹⁶ · a)² · a，也即 ((a⁸)² · a)² · a……最终简化为 ((((a²)²)²)² · a)² · a ，因而 7 次乘法操作就够了。在简化的过程中， a 的指数以成半的速度递减，因而在最后的式子当中，所需的乘法次数也是对数级别的，计算机完全能够承受。不过，减少了运算的次数，并没有减小数的大小。 a 已经是一个数十位上百位的大数了，再拿 a 和它自己多乘几次，很快就会变成一个计算机内存无法容纳的超级大数。怎么办呢？别忘了，“反正最后都要对乘积取余，相乘之前事先对乘数取余不会对结果造成影响”，因此我们可以在运算过程中边算边取余，每做一次乘法都只取乘积除以 n 的余数。这样一来，我们的每次乘法都是两个 n 以内的数相乘了。利用这些小窍门，计算机才能在足够短的时间里完成 RSA 加密解密的过程。

    RSA 算法实施起来速度较慢，因此在运算速度上的任何一点优化都是有益的。利用中国剩余定理，我们还能进一步加快运算速度。我们想要求的是 a³⁵ 除以 n 的余数，而 n 是两个质数 p 和 q 的乘积。由于 p 和 q 都是质数，它们显然也就互质了。因而，如果我们知道 a³⁵ 分别除以 p 和 q 的余数，也就能够反推出它除以 n 的余数了。因此，在反复平方的过程中，我们只需要保留所得的结果除以 p 的余数和除以 q 的余数即可，运算时的数字规模进一步降低到了 p 和 q 所在的数量级上。到最后，我们再借助“今有物，不知其数”的求解思路，把这两条余数信息恢复成一个 n 以内的数。更神的是，别忘了， aⁱ 除以 p 的余数是以 p – 1 为周期的，因此为了计算 a³⁵ mod p ，我们只需要计算 a^{35 mod (p-1)} mod p 就可以了。类似地，由于余数的周期性现象，计算 a³⁵ mod q 就相当于计算 a^{35 mod (q-1)} mod q 。这样一来，连指数的数量级也减小到了和 p 、 q 相同的水平， RSA 运算的速度会有明显的提升。

    需要注意的是， RSA 算法的安全性并不完全等价于大数分解的困难性（至少目前我们还没有证明这一点）。已知 n 和 e 之后，不分解 n 确实很难求出原始数据 a 。但我们并不能排除，有某种非常巧妙的方法可以绕过大数分解，不去求 p 和 q 的值，甚至不去求 m 的值，甚至不去求 d 的值，而直接求出原始数据 a 。不过，即使考虑到这一点，目前人们也没有破解原始数据 a 的好办法。 RSA 算法经受住了实践的考验，并逐渐成为了行业标准。如果 A 、 B 两个人想要建立会话，那么我们可以让 A 先向 B 索要公钥，然后想一个两人今后通话用的密码，用 B 的公钥加密后传给 B ，这将只能由 B 解开。因此，即使窃听者完全掌握了双方约定密码时传递的信息，也无法推出这个密码是多少来。

    上述方案让双方在不安全的通信线路上神奇地约定好了密码，一切看上去似乎都很完美了。然而，在这个漂亮的解决方案背后，有一个让人意想不到的、颇有些喜剧色彩的漏洞——中间人攻击。在 A 、 B 两人建立会话的过程中，攻击者很容易在线路中间操纵信息，让 A 、 B 两人误以为他们是在直接对话。让我们来看看这具体是如何操作的吧。建立会话时， A 首先呼叫 B 并索要 B 的公钥，此时攻击者注意到了这个消息。当 B 将公钥回传给 A 时，攻击者截获 B 的公钥，然后把他自己的公钥传给 A 。接下来， A 随便想一个密码，比如说 314159 ，然后用他所收到的公钥进行加密，并将加密后的结果传给 B 。 A 以为自己加密时用的是 B 的公钥，但他其实用的是攻击者的公钥。攻击者截获 A 传出来的信息，用自己的私钥解出 314159 ，再把 314159 用 B 的公钥加密后传给 B 。 B 收到信息后不会发现什么异样，因为这段信息确实能用 B 的私钥解开，而且确实能解出正确的信息 314159 。今后， A 、 B 将会用 314159 作为密码进行通话，而完全不知道有攻击者已经掌握了密码。

    怎么封住这个漏洞呢？我们得想办法建立一个获取对方公钥的可信渠道。一个简单而有效的办法就是，建立一个所有人都信任的权威机构，由该权威机构来储存并分发大家的公钥。这就是我们通常所说的数字证书认证机构，英文是 Certificate Authority ，通常简称 CA 。任何人都可以申请把自己的公钥放到 CA 上去，不过 CA 必须亲自检查申请者是否符合资格。如果 A 想要和 B 建立会话，那么 A 就直接从 CA 处获取 B 的公钥，这样就不用担心得到的是假的公钥了。

    新的问题又出来了：那么，怎么防止攻击者冒充 CA 呢？ CA 不但需要向 A 保证“这个公钥确实是 B 的”，还要向 A 证明“我确实就是 CA ”。

    把加密钥匙和解密钥匙称作“公钥”和“私钥”是有原因的——有时候，私钥也可以用来加密，公钥也可以用来解密。容易看出，既然 a 的 e 次方的 d 次方除以 n 的余数就回到了 a ，那么当然， a 的 d 次方的 e 次方除以 n 的余数也会变回 a 。于是，我们可以让私钥的持有者计算 a 的 d 次方除以 n 的余数，对原文 a 进行加密；然后公钥的持有者取加密结果的 e 次方除以 n 的余数，这也能恢复出原文 a 。但是，用我自己的私钥加密，然后大家都可以解密，这有什么用处呢？不妨来看看这样“加密”后的效果吧：第一，貌似是最荒谬的，大家都可以用我的公钥解出它所对应的原始文件；第二，很关键的，大家只能查看它背后的原文件，不能越过它去修改它背后的原文件；第三，这样的东西是别人做不出来的，只有我能做出来。

    这些性质正好完美地描述出“数字签名”的实质，刚才的 CA 难题迎刃而解。 CA 首先生成一个自己的公钥私钥对，然后把公钥公之于众。之后， CA 对每条发出去的消息都用自己的私钥加个密作为签名，以证明此消息的来源是真实的。收到 CA 的消息后，用 CA 的公钥进行解密，如果能恢复出 CA 的原文，则说明对方一定是正宗的 CA 。因为，这样的消息只有私钥的持有者才能做出来，它上面的签名是别人无法伪造的。至此为止，建立安全的通信线路终于算是有了一个比较完美的方案。

    实际应用中，建立完善的安全机制更加复杂。并且，这还不足以解决很多其他形式的网络安全问题。随便哪个简单的社交活动，都包含着非常丰富的协议内涵，在互联网上实现起来并不容易。比方说，如何建立一个网络投票机制？这里面的含义太多了：我们需要保证每张选票确实都来自符合资格的投票人，我们需要保证每个投票人只投了一票，我们需要保证投票人的选票内容不会被泄露，我们需要保证投票人的选票内容不会被篡改，我们还需要让唱票环节足够透明，让每个投票人都确信自己的票被算了进去。作为密码学与协议领域的基本模块， RSA 算法随时准备上阵。古希腊数学家对数字执着的研究，直到今天也仍然绽放着光彩。