这个 Blog 已经不止一次提到过难倒犹太人的“棺材问题”了。很多年以前，要想进入莫斯科国立大学的数学系，你必须通过四项入学考试；头两个都是数学考试，一个笔试，一个面试。在面试中，学生和考官都是一对一的，考官可以自由向学生提出任何他喜欢的问题。考官们都准备了很多“棺材问题”，这些问题的答案非常简单，但由于思路太巧妙了，以至于学生很难想到。考官便可以以“你连这个都没想到”为理由，光明正大地拒绝学校不想要的人（主要是犹太人）。之前我们曾经介绍过一个典型的“棺材问题”：空间四边形外切于给定球，求证四切点共面。去年的这个时候，我们还介绍了同样机智巧妙的 11 个问题。

    民间还流传着很多其他的“棺材问题”列表。 Ilan Vardi 曾经写过一篇题为 Mekh-Mat Entrance Examinations Problems 的论文，收集了 25 个“棺材问题”，并给出了解答。这篇论文被收录进了 You Failed Your Math Test, Comrade Einstein 一书中。 Ilan Vardi 发现，这 25 个问题的“难法”有所不同。虽然其中不乏思路奇巧的好题，但也有不少步骤繁琐（当然也有可能是还没找到好的解法）、题意不清甚至结论错误的题目。这里，我选择了其中五个有趣的题目，写下来和大家一同分享。

 

问题：是否存在无穷多个正整数对 (m, n) ，使得 m 和 n 用到的质因数完全相同，并且 m + 1 和 n + 1 用到的质因数也完全相同？

 

答案：存在无穷多对这样的 (m, n) 。令 m = 2^k – 2 ，不难看出 m 一定是偶数。再令 n = (m + 1)² – 1 。下面我们说明，这样的 (m, n) 是满足要求的。首先，由于 n + 1 = (m + 1)² ，显然 m + 1 和 n + 1 拥有完全相同的质因数。另外， n = (m + 1)² – 1 = m(m + 2) ，这表明 n 不但拥有 m 的所有质因数，还拥有 m + 2 的所有质因数。然而， m + 2 的所有质因数 m 都已经有过了，因为 m + 2 恰好是 2 的幂，所含的唯一质因数就是 2 ，而 m 是一个偶数，已经有质因数 2 了。因此， m 和 n 也拥有完全相同的质因数。
 
大家或许想问，除了这种形式以外，还有别的 (m, n) 也满足要求吗？有，不过不太好找了。例如， (m, n) = (75, 1215) 就是其中一个解。

 
 

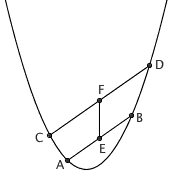
问题：给出 y = x² 的函数图像，用直尺和圆规画出两条坐标轴。

 

在函数图像上任取两点 A(a, a²) 和 B(b, b²) ，那么线段 AB 的斜率就是 (b² – a²) / (b – a) = a + b 。再在函数图像上取一个点 C(c, c²) ，过点 C 作 AB 的平行线，与函数图像交于另一点 D(d, d²) 。那么，线段 CD 的斜率也就是 c + d 。由于 CD 和 AB 平行，因而两条线段的斜率相同，由此可知 a + b = c + d 。现在，作出 AB 的中点 E ，作出 CD 的中点 F 。显然， E 和 F 的坐标分别为 ((a + b) / 2, (a² + b²) / 2) 和 ((c + d) / 2, (c² + d²) / 2) ，它们的横坐标是相同的。因此，线段 EF 和 y 轴平行。
 
   
 
接下来就容易了。作一条垂直于 EF 的直线，与函数图像交于 P 、 Q 两点。取 PQ 的中点 M 。过 M 作 EF 的平行线，这就是我们 y 轴。假设它与函数图像交于点 N ，则过 N 且垂直于 EF 的直线就是 x 轴了。

 
 

问题：证明，如果 a 、 b 、 c 分别是三角形的三边， A 、 B 、 C 分别是它们所对的角，那么一定有 (a + b – 2c) / sin(C / 2) + (b + c – 2a) / sin(A / 2) + (a + c – 2b) / sin(B / 2) ≥ 0 。

 

答案：不等式可以重新整理为 (a – b)(1 / sin(B / 2) – 1 / sin(A / 2)) + (a – c)(1 / sin(C / 2) – 1 / sin(A / 2)) + (b – c)(1 / sin(C / 2) – 1 / sin(B / 2)) ≥ 0 。下面我们说明不等式左边的每一项都是非负数，从而证明不等式恒成立。考虑到对称性，我们只说明不等式左边的第一项是非负的即可。由于三角形中大边对大角，小边对小角，因而若 a ≥ b ，则 ∠A ≥ ∠B ；另外注意到 ∠A 、 ∠B 的取值都在 0° 到 180° 之间，从而 A / 2 和 B / 2 都在 0° 到 90° 的范围内，于是 ∠A ≥ ∠B 可以推出 sin(A / 2) ≥ sin(B / 2) 。反过来， a < b 就说明 ∠A < ∠B ，也即 sin(A / 2) < sin(B / 2) 。因此， a – b 和 1 / sin(B / 2) – 1 / sin(A / 2) 一定是同号的，它们的乘积一定大于等于 0 。

 
 

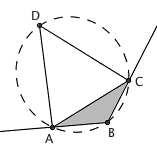
问题：已知三角形 ABC ， ∠A 和 ∠C 的外角的角平分线恰好交于该三角形的外接圆上。给定 AB 和 BC 的长度，求三角形外接圆的半径。注意，这是一个“有点特别”的问题。

 
   
 

 

答案：这是一个错题，题目中的条件根本不可能达到。一个三角形的两条角平分线根本不可能交在外接圆上。原因很简单，注意到 ∠BAD = (180° – ∠A) / 2 + ∠A = 90° + ∠A / 2 > 90° ，类似地 ∠BCD = (180° – ∠C) / 2 + ∠C = 90° + ∠C / 2 > 90° ，因此 ∠BAD + ∠BCD > 180° 。然而，如果 A 、 B 、 C 、 D 真的四点共圆，那么 ∠BAD + ∠BCD 应该等于 180° 才对，于是产生矛盾。

 
 

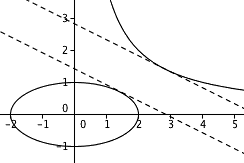
问题：已知 a² + 4 · b² = 4 ，c · d = 4 。求证： (a – d)² + (b – c)² ≥ 1.6 。

 

答案：我们要证明的其实就是，平面直角坐标系中的 (a, b) 和 (d, c) 两点的距离的平方大于等于 1.6 ，其中点 (a, b) 在椭圆 a² + 4 · b² = 4 上，点 (d, c) 在双曲线 c · d = 4 上。由于整个图像关于原点中心对称，我们只看椭圆与双曲线的其中一支即可。
 
   
 
不难验证，直线 y = – x/2 + √2 与椭圆相切，直线 y = – x/2 + 2 · √2 与双曲线相切。这两条直线的斜率相同，说明它们是平行的；这看上去就好像一条公路一样，椭圆位于公路的一侧，双曲线位于公路的另一侧。不难求出这条公路的宽度（即两条平行线之间的距离）为 2 · √2 / √5 ，从椭圆上的一点走到双曲线上的一点无论如何都必须要经过这条公路，因此其路程一定大于 2 · √2 / √5 。这说明 (a, b) 和 (d, c) 之间的距离不会小于 2 · √2 / √5 。这说明 (a, b) 和 (d, c) 之间的距离的平方不会小于 8 / 5 ，即 1.6 。