如果一个矩形可以分割为若干个小矩形，每个小矩形都有至少一边为整数长，则原矩形同样有至少一个长度为整数的边。换句话说，用至少有一边的长度是整数的小矩形拼成一个大矩形，大矩形也有至少一条整数长的边。

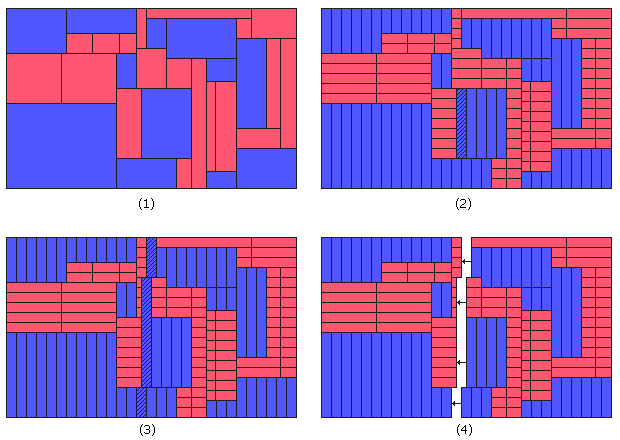
    我们首先把每个小矩形都分割成单位长或单位宽的长条。这样的话，大矩形里就只有两种小矩形：宽为1的（图(2)中的蓝色矩形）和高为1的（图(2)中的红色矩形）。我们对蓝色矩形的个数施归纳。随便选择一个蓝色的矩形（例如图(2)中的阴影矩形）。增加它的高度，让它“穿过”它头顶上的红色矩形（把它正上方的红色矩形截成左右两段），直到这根竖条状矩形的顶端碰到了另一个蓝色矩形的底端。把那个矩形作为新的操作对象，继续增加其高度（并可能再次更换“当前矩形”），直到达到整个大矩形的上边界。我们用同样的方法让最初所选的阴影矩形向下“生长”到大矩形的下边界。注意到在此过程中，蓝色矩形始终保持着单位宽度，红色矩形始终保持着单位高度。整个过程结束后，红色矩形变多了，但蓝色矩形的个数不变。此时我们得到了一条上下贯穿整个大矩形的蓝色矩形链。把它们擦掉，将右半部分左移一个单位，重新拼成一个大矩形。新的大矩形高度不变，宽度减一（因此原来的整数边还是整数，非整数边仍然不是整数），并且最关键的是蓝色矩形的个数减少了。反复进行这样的操作，总有一个时候大矩形里只剩下红色的矩形（则原大矩形高度显然为整），或者某次操作后所有矩形都被去掉了（则原大矩形宽度为整）。
    借用这种方法我们还可以得到一个有点搞笑的反证法。假设大矩形的横边竖边都不是整数。每一步操作后，这两个边仍然是非整数，这表明大矩形里不可能只剩一种颜色的小矩形，于是我们可以无限制地调用上面的操作。最后的结果是：我们得到了一个用整数长或整数宽的小矩形拼接而成的一个横边竖边都小于1的大矩形！这显然是荒谬的。

参考资料：http://www.cut-the-knot.org/Curriculum/Algebra/IntRectRobinson.shtml