我正在餐桌前吃早餐。餐桌上有一张圆形的大饼，有一个方形的蛋糕，还有一个甜甜圈。我依次思考了下面三个问题。你能帮我想出它们的答案吗？

• 3 刀切一张圆形的大饼，最多能把它分成多少块？或者说，3 条直线最多能把一个圆盘分成多少个区域？
• 4 刀切一个方形的蛋糕，最多能把它分成多少块？或者说，4 个平面最多能把一个正方体分成多少个区域？
• 3 刀切一个甜甜圈，最多能把它分成多少块？或者说，3 个平面最多能把一个（实心的）环面分成多少个区域？

提示：上一个问题的答案总会为下一个问题提供线索。

• 3 刀切一张圆形的大饼，最多能把它分成多少块？或者说，3 条直线最多能把一个圆形分成多少个区域？

​

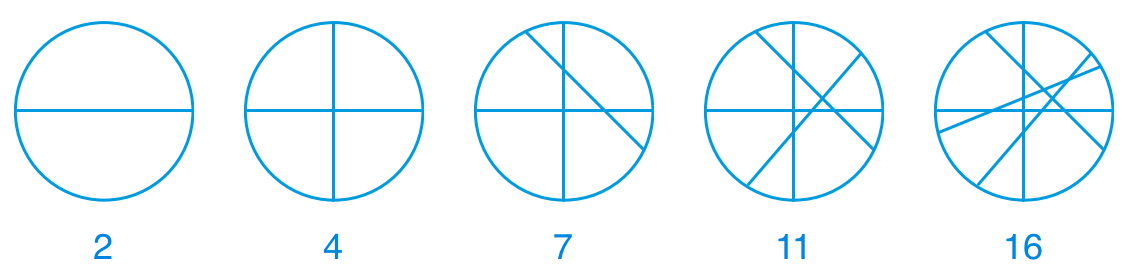
这是一个经典的小学问题。答案是 7 块。如图所示，事实上，当直线数分别为 1, 2, 3, 4, 5, …时，最多产生的区域数对应地是 2, 4, 7, 11, 16, …。这背后的规律是：1 条直线能把圆盘分成 2 个区域；第 2, 3, 4, 5, …条直线，则会让区域数增加 2, 3, 4, 5, …个。

1 条直线最多能把圆盘分成 2 个区域，这事儿很显然。为什么第 n 条直线会让区域数增加 n 呢？这背后有一个非常简单的解释。前 n − 1 条直线会与第 n 条直线产生最多 n − 1 个交点，把第 n 条直线切成最多 n 段。仔细想想第 n 条直线上的每一段意味着什么——意味着某一个原有区域被细分成了两个新的区域，它们以这条线段为公共边界，分居这条线段两侧。所以，第 n 条直线最多被切成 n 段，就说明总的区域数在原来的基础上最多会增加 n。

• 4 刀切一个方形的蛋糕，最多能把它分成多少块？或者说，4 个平面最多能把一个正方体分成多少个区域？

​

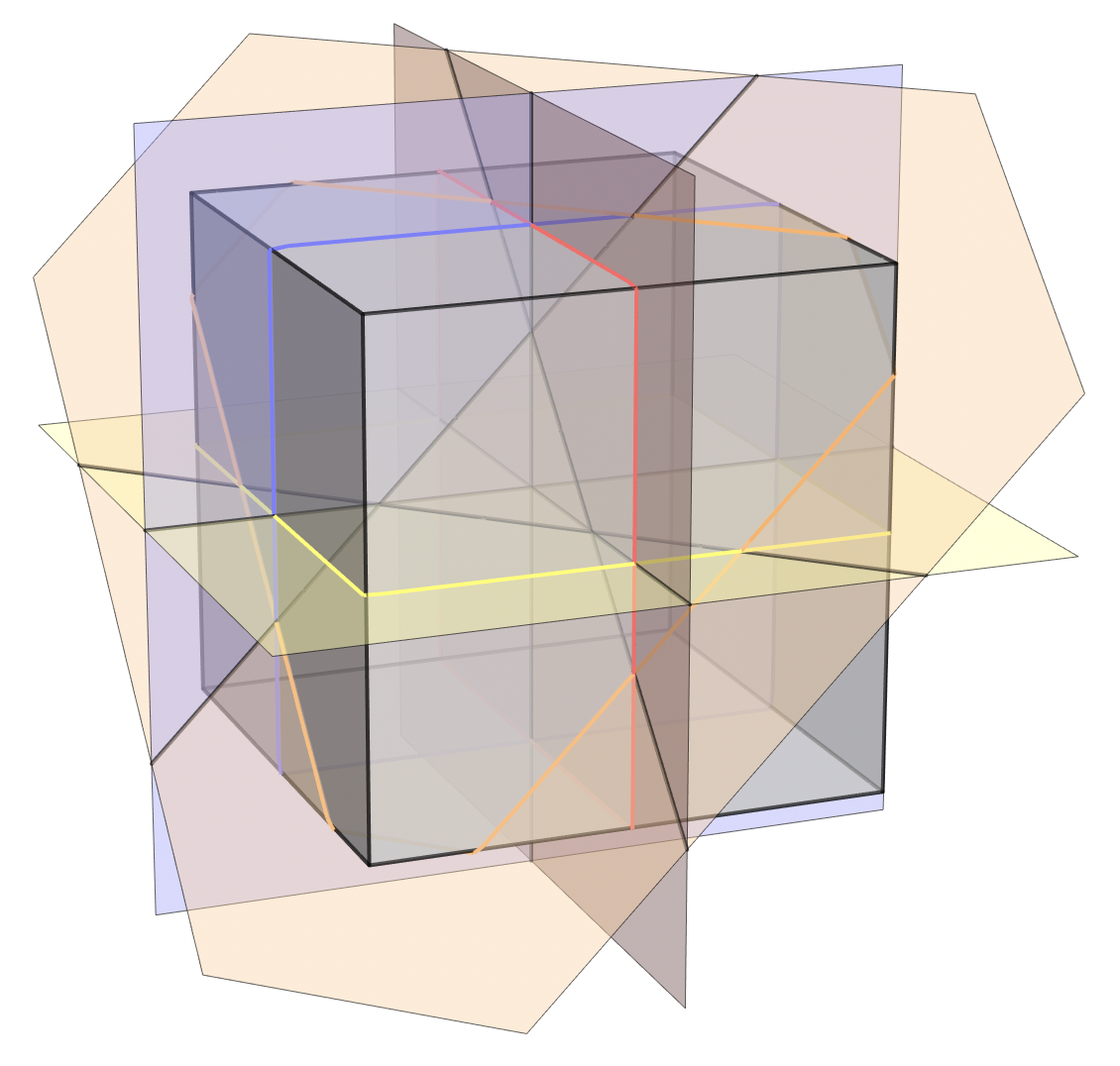
答案是 15。其中一种构造方案如下。前 3 个平面是三个两两垂直的平面，它们交于正方体的中心。整个正方体就被切成了 8 块小正方体，其中上层有 4 块，下层有 4 块。第 4 个平面不过整个正方体的中心，并且跟前 3 个平面都不平行，如图所示。

​

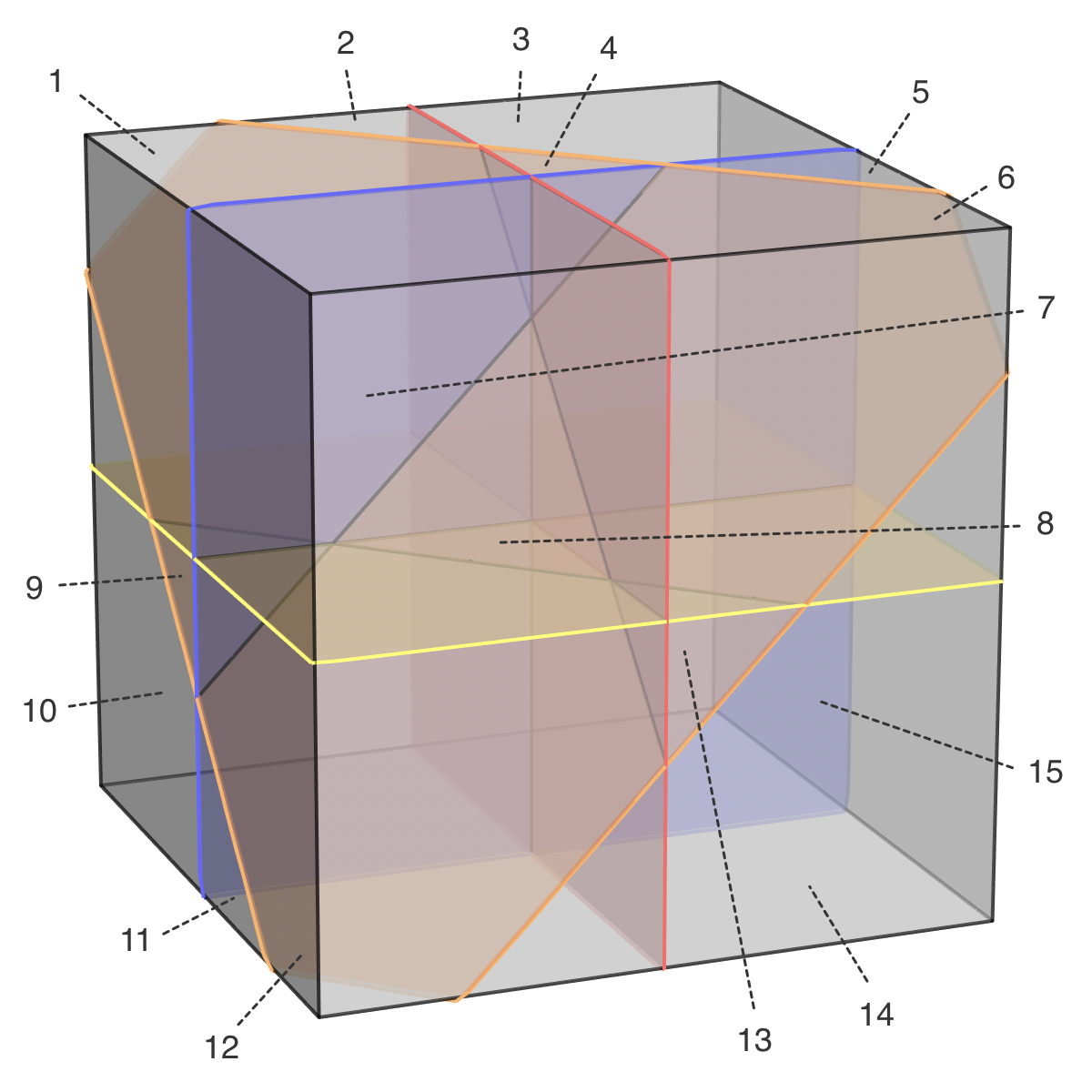
于是，上层的每个小正方体都被分成了两个小的区域。位于“上左前方”的那个小正方体有些特殊，它被分成 7 号、8 号区域，其中 8 号区域是一个位于内部的四面体区域，它的四个面都是新切出来的。但是，下层只有其中三个小正方体被分成了两个小的区域。第 4 个平面错过了位于“下右后方”的那个小正方体，它没有被细分成两个小的区域，在图中我们用 15 号区域来标记。

通过这个例子，我们看到，4 个平面有可能把正方体分成 15 个区域，但为什么这就是最多的了呢？首先，3 个平面最多把正方体分成 8 个区域，这事儿应该还是挺直观的，我们干脆就把它直接当结论了。关键的问题就是，第 4 个平面为什么最多只能让区域数增加 7。前面那个切大饼的思路和答案，在这里都会派上用场。

​

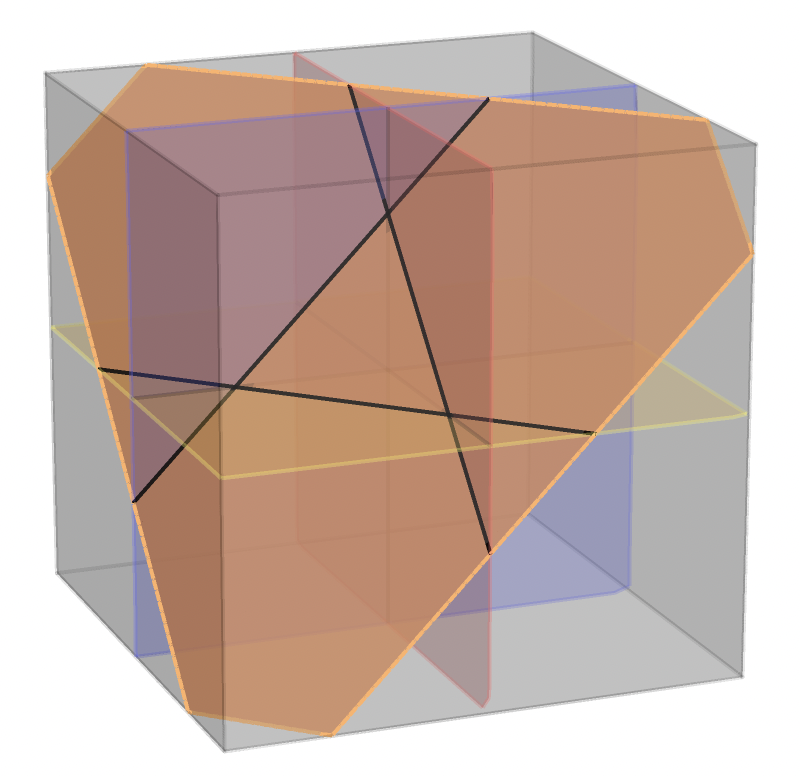
分析切大饼时，我们的思路是，把目光集中在最后这条直线上；受此启发，在这里，也让我们看一看第 4 个平面上发生了什么。前 3 个平面在第 4 个平面上产生了 3 条交线，这 3 条线在该平面上最多划分出 7 个多边形（这算是直接用到了切大饼问题的答案）。每一个多边形都意味着，大正方体中原来的某个区域，现在被分成了两个小区域。有 7 个多边形，就意味着新增了 7 个区域。

据此容易得出，只要这 4 个平面满足任意两个平面不平行，任意两条交线不平行，且 4 个平面不过同一点，分出的区域数都能达到最大值。当然，这有个前提：这些平面必须得交在正方体内才行。

• 3 刀切一个甜甜圈，最多能把它分成多少块？或者说，3 个平面最多能把一个（实心的）环面分成多少个区域？

​

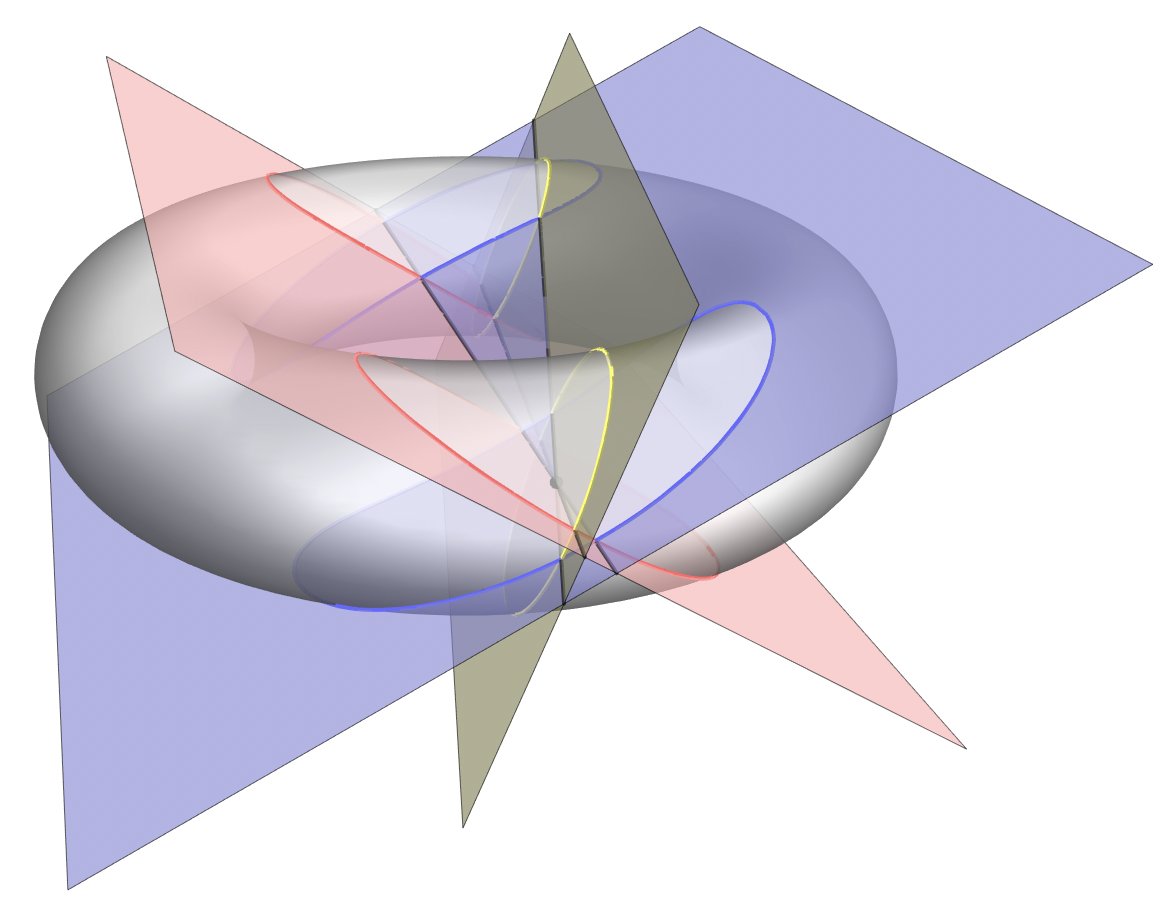
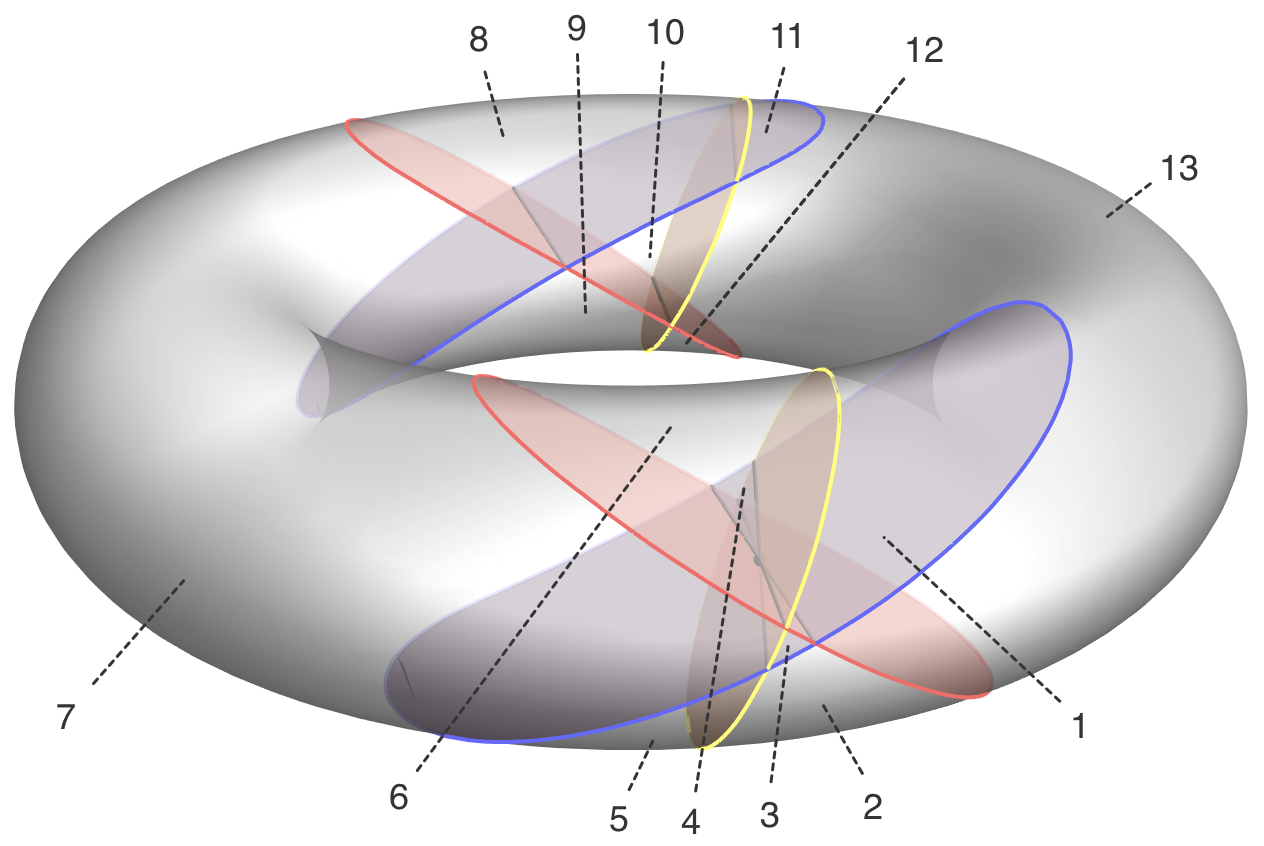
答案是 13。其中一种构造方案如下。过位于实心部分内的某一点 P 作 3 个方向互不相同的平面，平面之间产生 3 条不同的交线，每个平面都把环面切成了两个 C 字形。这就会带来 13 个不同的区域。其中 3 号区域和 4 号区域是两个近似的小三棱锥，它们都以 P 为顶点，侧面都是新切出来的，“底面”实际上都是曲面。

​

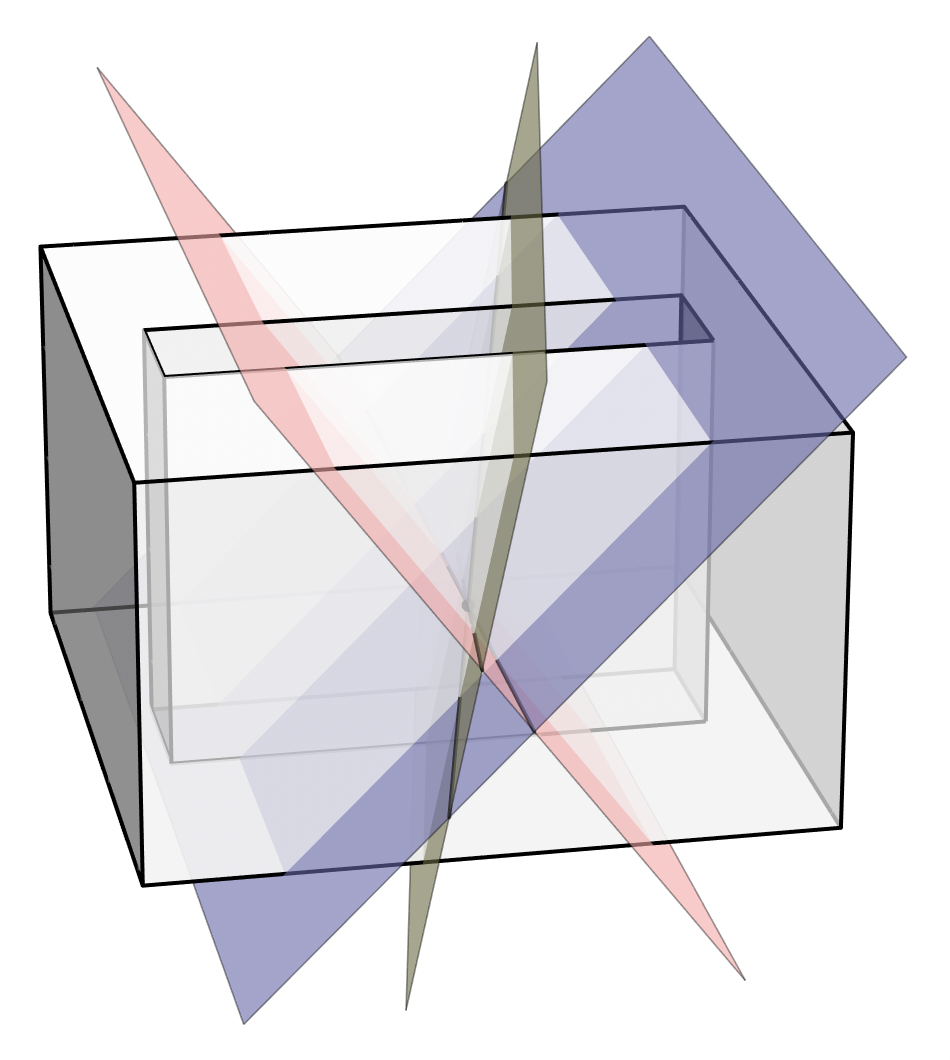
3 刀切甜甜圈的问题，和之前 4 刀切蛋糕的问题，之间有着直接的联系。事实上，前者的答案一定等于后者的答案减 2。理由很简单。我们可以把实心的环面想成是一个中间有孔的蛋糕，而这个孔又可以想象成是预先在蛋糕上切了特别粗但是没通到边儿上的一刀。所以，3 刀切甜甜圈的问题，等价于 4 刀切蛋糕的问题，只不过其中一刀没有把蛋糕切断。如果这一刀两头向外延伸，真的把蛋糕切断了，会在两头各增加一个新的区域，得到 15 个区域；但是，这一刀并没有把蛋糕切断，所以所得的区域数要减 2，只有 13 个区域。

​

切大饼和切蛋糕问题都是经典问题。我最近在这里看到了切甜甜圈的问题。看到这个问题之后，我的第一反应就是，切甜甜圈也是一个非常自然的问题，为什么我就没有提出来过呢？这个问题的一个比较早的出处是 Martin Gardner 所著的 The 2nd Scientific American Book of Mathematical Puzzles and Diversions。书中给出了一个 3 刀切甜甜圈切出 13 块的示意图：

​

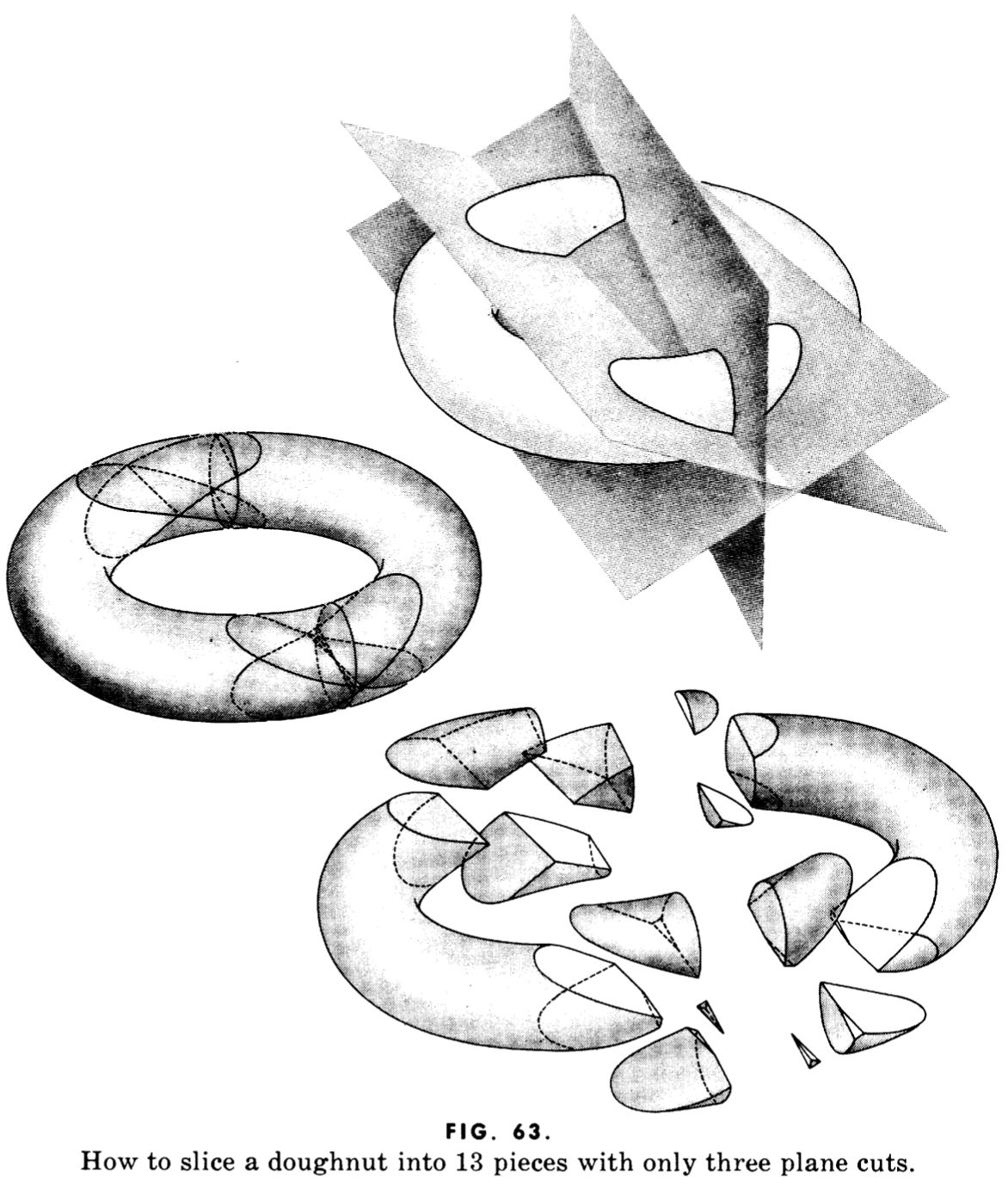
书中还给出了 n 刀切甜甜圈最多能切出多少块的公式：(n³ + 3n² + 8n) / 6。但书中没有说明背后的道理。本文讲到了切甜甜圈和切蛋糕之间的神奇联系。这是我在这里看到的。利用这种联系，不难推出上述公式。这个问题显然还有很多进一步扩展、推广的空间。有空我会继续思考，并查阅更多的资料。

2021 年 9 月 13 日更新：其中一个插图有误，已更换
2021 年 9 月 16 日更新：补充了切蛋糕问题中区域数达到最大值的条件