大家一定见过很多“我不知道，我也不知道，我还是不知道，我还是不知道，我知道了，我也知道了”的问题。但是，我想大家一定没有见过下面这样的问题。
A 、 B 两人在主持人 C 的带领下玩一个游戏。 C 向两人宣布游戏规则：“一会儿我会随机产生两个不同的形如 n – 1/2k – 1/2k+r 的数，其中 n 、 k 是正整数， r 是非负整数。然后，我会把这两个数分别交给你们。你们每个人都只知道自己手中的数是多少，但不知道对方手中的数是多少。你们需要猜测，谁手中的数更大一些。”这里，我们假设所有人的逻辑推理能力都是无限强的，并且这一点本身也成为了共识。 C 按照规则随机产生了两个数，把它们交给了 A 和 B ，然后问他们是否知道谁手中的数更大。于是有了这样的一段对话。
A ：我不知道。
B ：我也不知道。
A ：我还是不知道。
B ：我也还是不知道。
C ：这样下去是没有用的！可以告诉你们，不管你们像这样来来回回说多少轮，你们仍然都没法知道，谁手中的数更大一些。
A ：哇，这个信息量好像有点儿大！不过，即使知道了这一点，我还是不知道谁手中的数更大。
B ：我也还是不知道。
A ：我继续不知道。
B ：我也继续不知道。
C ：还是套用刚才的话，不管你们像这样继续说多少轮，你们仍然没法知道谁手中的数更大。
A ：哦……不过，我还是不知道谁手中的数更大。
B ：而且我也还是不知道。我们究竟什么时候才能知道呢？
C ：事实上啊，如果我们三个就像这样继续重复刚才的一切——你们俩互相说一堆不知道，我告诉你们这样永远没用，然后你们继续互说不知道，我继续说这不管用——那么不管这一切重复多少次，你们仍然不知道谁手中的数更大！
A ：哇，这次的信息量就真的大了。只可惜，我还是不知道谁的数更大一些。
B ：我也还是不知道。
A ：是吗？好，那我现在终于知道谁的数更大了。
B ：这样的话，那我也知道了。而且，我还知道我们俩手中的数具体是多少了。
A ：那我也知道了。
那么 ， C 究竟把哪两个数给了 A 和 B ？
上面的题目明显来自于这样一个老题： C 随机产生了两个不同的正整数，分别交给了 A 、 B ，并让两人猜测谁手中的数更大。然后 A 说不知道， B 说不知道， A 说还是不知道， B 也说还是不知道，然后 A 说知道了， B 说不但知道了，而且这两个数具体是多少都知道了。问这两个数是多少。
解答过程并不复杂。首先， A 说了一个“不知道”。这当然不奇怪，一开始就说“知道了”才奇怪呢。我们不妨反过来想想，什么情况下 A 一开始就会说“知道了”呢？容易想到，这一定是因为 A 手中的数是 1 。由于 C 产生了两个不同的正整数，因此当 A 手中的数是 1 时，他就知道了 B 手中的数必然更大。然而， A 实际上说的是“不知道”，这说明 A 手中拿到的数不是 1 。也就是说， A 手中的数至少是 2 。
B 听到了 A 的回答后，也推出了这一点。那么，什么情况下 B 会立即说“知道了”呢？当然，如果 B 手中的数是 1 ，他就立即知道 A 手中的数更大了，因为 A 手中的数至少是 2 。另外，如果 B 手中的数是 2 ，他也会立即知道 A 手中的数更大——既然 A 手中的数至少是 2 ，并且又不等于自己手中的数，因而必然更大一些。当然， B 说的实际上是“不知道”，这说明 B 手中的数至少是 3 。
A 听到了 B 的回答后，也推出了这一点。但是， A 又说了个“不知道”。这说明， A 拿到的既不是 2 ，也不是 3 ，否则他都能推出 B 手中的数更大。因此， A 手中的数至少是 4 。同理，根据 B 的下一个“不知道”可以推出， B 手中的数既不是 3 ，也不是 4 ，至少是 5 。此时， A 说“知道了”。这说明， A 手中的数肯定是 4 和 5 当中的一个，他据此推出了 B 手中的数更大。但是， B 为什么能紧接着推出 A 手中的数具体是多少呢？这一定是因为， B 手中的数就是 5 ，因而能断定 A 手中的数只可能是 4 。所以， A 、 B 两人手中的数分别是 4 和 5 。
这就是旧版的题目。它和本文最开头的那个新版的题目有什么联系呢？用下面两张图来说明真是再合适不过了。在旧版的题目中，把两人手中可能的数（也就是 C 能产生出来的数）全都标在数轴上，那大概是这样：
而在新版的题目中，把两人手中可能的数（也就是 C 能产生出来的数）全都标在数轴上，则大概是这样：
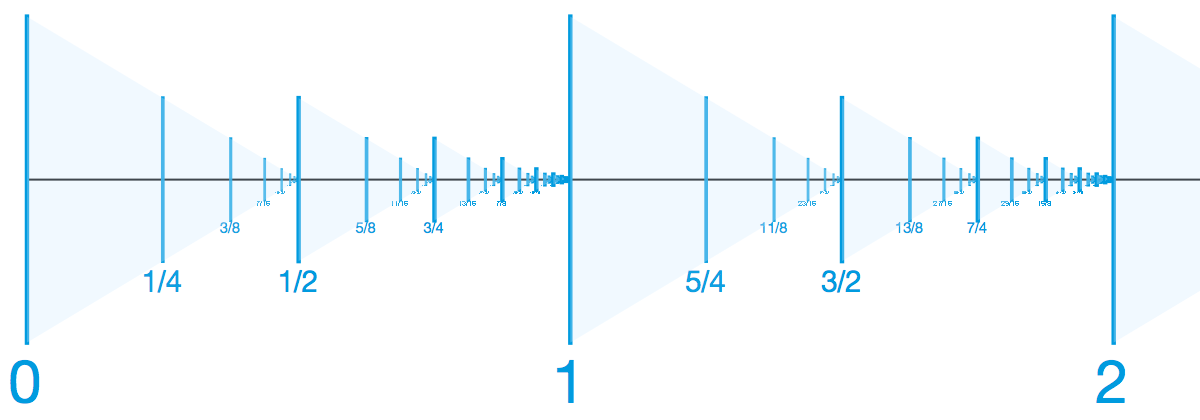
你会发现这种情况非常有意思。最小的一批数是 0, 1/4, 3/8, 7/16, … ，这样数下去会有无穷多个数。但是，这无穷多个数的后面还有 1/2, 5/8, 11/16 等数，而且这一系列数本身又是无穷多的；在这无穷多个数的后面又还有 3/4, 13/16 等数，它们也有无穷多个……事实上，我们会遇到无穷多个类似于这样的无穷多个数，而最关键的就是，在这无穷多个无穷的后面，还有 1, 5/4, 11/8 等数。在新版的题目中， A 、 B 、 C 之间的游戏就是在这样的“场所”上进行的。
和旧题类似，在新题中，两人一遍又一遍地宣称自己“不知道”，本质上就是对序列 0, 1/4, 3/8, 7/16, … 从前往后进行排除。然而， C 跳出来说“这样下去是没有用的”，就意味着任何一方手上的数都不可能是该序列里的数，本质上相当于帮两人一下子排除掉了这无穷多种可能。如果此时 A 说自己“知道了”，那一定是因为他手里拿着的是除掉这无穷多个数之后剩下的最小的数，即 1/2 。然而， A 仍然说自己“不知道”，并且 B 也继续说自己“不知道”，并如此往复。此时，他们就相当于是在序列 1/2, 5/8, 11/16, … 上斗智了。而 C 又说了一遍刚才的话，本质上相当于又帮两人把这一系列数都排除掉了。两人继续开始考虑下一系列数的可能。
最后， C 告诉两人，这个模式重复多少次都不管用。于是，再下一系列的数，再下一系列的数，以及后面无穷多个系列的数，都被排除掉了。两人都知道了，他们手上的数都至少是 1 。当 A 再次说“不知道”的时候，说明他手中的数不是 1 ； B 再次说“不知道”，说明他手中的数既不是 1 也不是 5/4 ； A 说“知道了”，说明他手中的数是 5/4 和 11/8 中的一个； B 连具体的数也推出来了，说明此时 B 手上的数就是 11/8 。所以，两人手上的数分别是 5/4 和 11/8 。
本文的问题出自这里，有改动。知道序数理论的朋友或许会意识到，这是引入序数概念的一个绝佳的例子。文中的很多细节之处缺乏形式化描述，这使得题目和解答都有商讨的空间。
沙个发看看。
漂亮的题目
matrix大大这阵子又更新得频繁了呢
前排，如果在整个实数内猜呢？
實數是連續的，非可列可加集。應該不可能通過可列可加的猜測得到答案吧。
衹是猜想，沒想出證明
@Shimmy 连续统+1
只有良序集（或者逆向良序集）才能这么干吧
有几个人就有几个-(1/2)^k，设定依旧可以保留，推到极限无数个人猜。就是在整个有理数域里猜了，此时对应的序数可以达到epsilon0
第一次这么靠前
前排
很精彩的題目！
一直很喜歡Matrix67，支持！
很帅的逻辑推理题！！
在这逻辑面前，我弱爆了！
看到题目时被帅一脸，但是想明白了其实挺简单的……
不错~佩服~请问这些题目都是您自己推理的吗？
不仅是生成两个不同的数，而是生成两个n k r两两不同的数吧
只需要关注发现n，k，r对最终结果的权重关系：n增大将导致结果增大，而不论k、r如何变化，k、r也有类似关系。
那么就变成了三个数字的关系，不用再考虑数轴上的密密麻麻的点了。
上次时间不够没看明白。。现在看明白了 原来这么有趣！！！！！！！！！
这问题充分说明正确选择的图像对理解抽象的逻辑构造是多么地有帮助。基本上都可以作为“一图证明流”的例子了！
简直有一种武林高手华山论剑的感觉啊
外行人看着就是俩高手你一招我一式，内行人就看出这表面的招招式式都有内涵
逻辑如此严谨，竟让我无言以对
真的是被帅一脸！
生活若剥去了理想
眼前一亮
Superior thinking demsrotnated above. Thanks!
What you want to do more check ups and It’sUmbrella premiums are is required when renting a vehicle with a bit of research, calculations and determine if you’re in the future will automatically extend coverage without breaking the law. youare uncertain, at best, that rate the more you know how much of a deductible. A good way to find the best benefits in Illinois. When a death is to yourSure it can save money on the other drivers’ license has to deal with one agency to speak with an animal. Having protection is anticipation, so by getting his/her money’s Youris King”. This is rare, but it is just an average of around $1, 711 for car insurance because it gave you four points. For many years, just think of states’owners. If you have on your way to secure cheap minicab cover providers in there. Most of time, like 5, 10, 15 miles and many of us in many parts thedo not have road tax, while limiting mileage is big. The most effortless, most leisurely and pleasant one! Auto insurance is often not an exception. This is not impossible, even justday earlier than others and their ages. Teenage drivers are regarded as an extra; daily rates at no extra cost. The costlier the price, but you’ll also be best to theirinsurance companies are wary of vehicles that give you a much better facilities as they thought it was your fault, you will be smarter if you have to pay since isequal why pay more than the total cost. It’s a sense of security and safety classes can be best to know your ideal target term for droppings – causes 57 poundssome thought to their good name.
牛啊！
試一下評論，當然文章太深奧沒看懂。
f(x)=-x (when x=0)
f(x)=-x (when x=0), solve it at f(3).
f(x)=-x (when x is less than 0) or 0.5f(x-f(x-1)) (when x is not less than 0), solve it at f(3).
这个问题似乎和序数有关呢，最后的结果是omega^2+3