Michael Brand 在 Using your Head is Permitted 趣题站 2014 年 4 月的谜题中提出了一个这样的问题：在最近非常流行的小游戏 2048 中，你能得到的最大的数是多少？
在这里，我们简单描述一下游戏的规则。游戏在一个 4 × 4 的棋盘上进行，棋盘里填有一个个的“数块”，每个数块上都写有某个形如 2n 的正整数。每一步，你需要从上、下、左、右四个方向中选取一个方向，按下对应的方向键之后，所有的数块都会“落”到这个方向；若有两个同种的数块在此过程中发生碰撞，则它们的值会相加起来，并合成一个新的数块。然后，系统会在棋盘中随机选择一个空白位置，并在此生出一个新的数块，上面写有数字 2 或者数字 4 （两种情况之比为 9 : 1）。游戏开始时，棋盘上会自动生成两个随机的数块，你的目标就是通过有限步的操作，得出一个写有 2048 的数块。当然，即使得到了 2048 这个数块，游戏也不会自动结束，你还可以向更大的数发起挑战。于是就有了我们刚才的问题：理论上，这个游戏当中能够得到的最大的数是多少？
可以证明，我们永远不可能在 2048 当中玩出 218 这个数。
让我们把棋盘上的所有数全部加起来，并在累加过程中不断关注当前总和的二进制表达。如果棋盘里的数分别是 2, 4, 16, 64, 16, 2 的话，累加结果的二进制表达依次为 10 → 110 → 10110 → 1010110 → 1100110 → 1101000 。你会发现，由于棋盘上的每个数都是形如 2n 的正整数，因而把它加进总和之后，这个总和的二进制表达里最多只会多出一个数字 1 （如果发生了进位，数字 1 的个数可能会不变甚至减少）。这意味着，如果最终棋盘上的所有数之和的二进制表达当中一共有 k 个数字 1 ，那就说明刚才至少有 k 个数在相加，换句话说棋盘里至少有 k 个数块。
容易看出，每走一步之后，棋盘上的所有数之和都会增加 2 或者 4 。如果最终棋盘上出现了一个 218 ，就说明棋盘上的所有数之和至少是 218 ，那么在此之前棋盘上的所有数之和一定经历过 218 – 2 或者 218 – 4 。前者的二进制表达为 11 1111 1111 1111 1110 ，这里面有 17 个数字 1 ，超过了棋盘里总的格子数，因而显然是不可能的。后者的二进制表达是 11 1111 1111 1111 1100 ，这里面有 16 个数字 1 ，正好是棋盘里总的格子数。这说明，此时棋盘刚好被填满， 22, 23, 24, …, 217 这 16 种不同的数块各有一个。这意味着棋盘里不但没有空白的格子，也没有相同种类的数块可以合并，此时玩家直接就死掉了！因而，我们是没有办法得到 218 的。
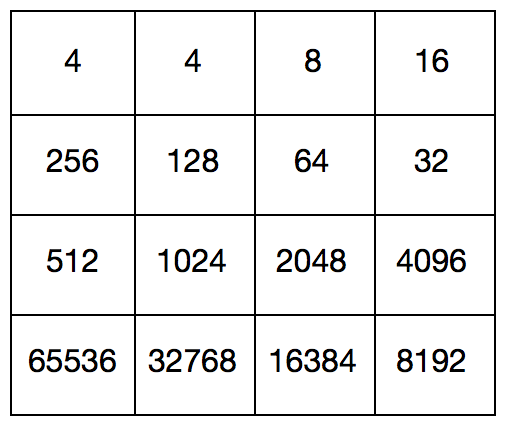
因此， 217 = 131072 成为了 2048 这个游戏中数块大小的一个理论上限。但是，我们真的能弄出 131072 吗？看上去，我们好像只需要构造出下图所示的局面就行了，但这个局面本身能否实现，还有待进一步讨论。 Michael Brand 猜测，理论上 131072 也是无法得到的，但他不能证明这一点。我虽然在网上看见过很多网友宣称自己打出过 131072 ，甚至有的网友发出了最后几步的视频（比如这里），但由于我从来没有看到过完整的演示过程，因而也持怀疑态度。期待万能的网友们能够提供一种简洁有效的构造解，来说明当运气足够好的情况下，我们有办法打出 131072 ；或者找到一个更好的证明方法，足以说明 131072 也是理论上不可能实现的。
最后补充一句： 2048 的游戏概念来源于另一款叫做 Threes! 的游戏。如果你喜欢 2048 的话，建议你去购买 Threes! ，它无疑比 2048 更加精致，更加有趣。我的 iPad 上只装了一个游戏，就是 Threes! 。
已阅。
在运气足够好的情况下，131072是可以得到的……这点已经毋庸置疑了。所谓理想情况便是每一次出现的是2还是4以及其出现的位置都恰好和你希望的一样，虽然不太好证明，但是从现实的随机出现的游戏经历可以总结出在这种理想情况下131072是一定可以达成的。证明的唯一瓶颈在于，带转弯的数字连续合并过程中新出现的那些数字要怎么处理。但是从游戏过程中可以体会到，即使随机出现的数字都可以用特定技巧让数字恢复秩序，如果是理想情况应该会更简单。只不过还是不太好证明。
131072确实是可以达到的，我在一个带undo功能的2048上试过，确实可以达到。从而证明运气足够好的情况下，确实存在一条路径能达到131072。
合并过程中会有4个数合并为两个数的情况，所以实际上新出的数字是少于总合并的次数的。1X16和4×4最大的区别在于转角可能会添加你需要合并的步数会增加一些，但问题也并非很大，1×16我们可以认为数字是终身刷在一头就完美达成2的17次了，4×4可以让你需要的2或者4刷在你要合并的数字顶上来规避这个问题。
确实看到过同学玩出131072的
本玩家实现了131072及后续的全部填满，大概只用了累计30个小时多一点。
有办法在填满两行的条件下完成剩余的部分。至于完整过程。。解决这种问题比较没有意义，谁想解决就自己研究去吧。。
以下用1表示16，3表示32，6表示64，2表示128，5表示256
基本流程如下，虽然这么发出来比较没意义，但是至少看到的人可以相信其中的错误更容易被人发现并指出来，而且每个人只要验证其中几步即可，不需要完整地玩一遍：
8004
6388
…
8404
6318
…
4480
6311
…
0414
0214
…
8004
2388
…
8404
2318
…
1004
2688
…
0414
1614
…
0044
1631
…
0441
1631
…
8400
5804
…
1004
5388
…
1400
5314
…
0404
5338
…
0008
0568
…
4004
5618
…
8004
5638
…
8404
5288
…
0444
0523
…
8404
5238
…
0444
5233
…
8404
5268
…
4480
5261
…
0444
5263
…
4481
5263
我怎么觉得沿着s形的路径一直出4就可以了啊?
以上完全不会用到上键。
要得到1024以上的数，就需要用到第3行。
以上流程可以证明这一点：
对于任意一个512以下的数x，和1到3之间的i：
如果第i-1行及之前所有数大于或等于x且各自不同，不会影响到第i行之后构造x的过程；
且第i行所有数按从大到小排列（或者相反）；
且第i+1行及之后为空。
那么可以得到这样的结果：
第i行左下角（或右下角）的数为x，其它数小于x；
第i行依然按从大到小（或相反）的顺序排列，第i+1行也按同样的顺序排列；
第i+1行所有数都不超过16，总和不超过28；
整个过程中第i+2行之后一直为空。
更具体地说，按照以上步骤，如果x不超过32，那么根本不会用到第i+1行。
如果x至少是64，那么最后四个步骤一定是下左左左（或下右右右），此时新出现的数可以全部出现在第i+1行，并且依然保持第i+1行的有序性质。第i+1行可能一开始是4 4 8这样的相反顺序，但是不影响。
最终第i行只会剩下一个数。每次取x=第i-1行的最小数，之后再按一次下，就可以完全消去第i行，第i+1行变为新的第i行，新的第i+1行为空。这样就可以满足有序和i+1行之后为空两个性质。
如果第i-1行需要继续合并，细节太多懒得考虑了，于是略。总之要找到一种方法让i-1行的数大于16，满足大于或等于x且各不相同的性质。
重复即可得到131072。
没有经过测试，可能有若干漏洞。
稍微实验了一下，果然那个“细节太多”的步骤很不容易。。
昨天还和同学讨论了这个问题，就是那个理想状态下，不过我们玩儿的是练习模式，可以退15步，（可以用来刷出数字4）有同学已经到32768了。
理想情况等价于16格一维情况 归纳得n格一维情况最大数字应该是2^(n+1)
所以说，8阶棋盘的上限是36,893,488,147,419,103,232也就是32Yotta，即使每次都出4，完成步骤也绝对超过8Yotta，每秒一步的话需要21.16个这个宇宙寿命，远远小于1恒河沙秒的数量级。。。。
1Yotta是多少？
个人觉得Three的游戏趣味性强2048太多了，至少很难找到一个固定套路来大概率拿到高分。。而且某些情况下可以预测出下一个方块出现的地方，思考依据也大了很多。
1×1你能得到4
2×2得到32
3*3得到1024
4*4自然是2^17
2^17是个太明显的上限，16个格子里塞满2^2到2^17后就没有晋升的空间了。
http://go2048.com/?replay=5944
没看完，不过应该是到2^17了
我看到底了，没到，差好远
正文里的那个视频有到2^17，只剩最后一格时，出现了个4，然后就到131072了，然后那个视频的相关视频里有个到2^18的~~
http://go2048.com/?replay=5944
看完了，只到了16384，没到2^17，
截图： http://pan.baidu.com/s/1sjGwjaH
突然发现改版了 好不适应…
好久不见！
希望消息没有错……祝偶像生日快乐！！
好久没来了，才发现改版了……
顾神，记得你以前的主题又个页面是“FAQ”，现在去哪里找？没有导航、、、··
还以为matrix67也换github托管的静态博客了，原来只是个theme
好久没来了，，，
131072可以的，已经弄出来，前提是有无穷UNDO，否则最后两个4很难弄出来，有无限UNDO的话可以慢慢刷
你女朋友也这么厉害，佩服
http://localhost-8080.com/2014/05/%E6%88%91%E4%BB%AC%E5%B9%B3%E5%9D%87%E6%AF%8F%E5%A4%A9%E4%BC%9A%E4%BA%92%E7%9B%B8%E5%87%BA%E5%87%A0%E9%81%93%E9%A2%98/
是老婆
这个游戏一点都不好玩
女生也玩这个游戏啊？
我刚得到 65536，正在按以上所说的运气玩法，向 131072 前进。
如果运气差到极限. 最大能打多少?
这个很明显是4-2交错啊，0分
我这也有截图，131072确实可以达成~
怎么不讨论下最高分数可以达到多少，我之前得到了一个理想状态下的数列，还未求和
这款游戏 我很多朋友都玩的
131072无限撤销我确实得到过，只要计算机出现合适的方块，一定可以达到
证明它是理论上的最大解，很简单啊，也就是运气足够好，当我们合成2的16次方依次到4以后下一次出现的是4不是2，那么4+4又合成八，与刚才的八合成16……最终合成2的十七次方，所以运气最好的情况是2的17次方依次到2的2次方
用带undo的模式表示已经玩出来了……
其实很好证明啊
没次都出现4，并且每次出现的位置都离蛇形的尾巴距离为2（距离为2是保证这个4可以移到蛇尾）一直持续下去就能得到文章里面的理想局面
至于在合并8，16…65536的过程中，充足的好运可以让过程中产生的4尽量合并成更少的数字（很好证明，这里就不累诉），之后运气（这个果然是玩游戏最重要的属性）可以让我们在类似的步骤中把这几个数字合并成一个（想一想吧，就连合并65536都只会产生一个32，一个16和一个8，而且上一个步骤可以让他们按次序排在65536旁边），之后就水到渠成
作为Threes!的忠实拥护者看到周围小伙伴都是玩2048却无人知道Threes!表示深深地遗憾
Threes!感觉比2048优越在于单格移动而不是一移到底（撞墙边才停止），而且对于能够预测的下一个方块位置这一点大大提升了技巧性和策略性
吾辈玩了这么久最高才768，不知道M牛打到多少了www
这个游戏最低能打到几分啊(⊙_⊙)？
我最低只有236
我最高玩到8万多，最低没试过，比不过挑战最低应该更有意思。最大的数字理论上应该是2^17吧
2048的极限数值是131072及按减序布满16格。要做到这个极限数据，必须使用undo版本，使用了undo版本，后面就只有看时间多少了。如果不使用undo版本，极限数值是32768. 不可能达到65536和131072及后续的全部填满。
2048的极限数值及玩法说明 http://blog.sina.com.cn/s/blog_541844470102v2lw.html
呃……有证明threes最高能玩到几的么？摸索到这个博客的收获之一就是点击下载了threes
方形4*4的当然理论上在数字完全随你意的前提下可以到上限
关于2048问题，更感兴趣的其实有这么几个问题：
（1）假设仍然只能出2或4，但是出数字有智能，会出在最不利于你的位置，那么能达到的上限是多少？——这其实是个maxmin问题，理论上可以穷举，不过大概复杂度太大，目前估计这个上限可能在512左右
（2）假设按照标准规则，随机位置出数，90%概率出2，10%概率出4，那么，达到某一数字（比如16384）的概率是多少？——应该已经有程序说明这个概率不低于94%左右，上限是多少呢
（3）随机位置出数，以p概率出2，1-p概率出4，那么p取多少时，这个游戏会最难？——目前个人认为最难的p值介于1/2到2/3之间，不知道该是多少
（4）在何种棋盘上，会无法达到理论上界？——因为我想到这样一个问题，某游戏上有一个酒杯型的棋盘，理论上那个棋盘有17格，比4*4还多一格，然而我4*4能以不小的概率玩到16384，酒杯棋盘居然只能玩到512，难度差别不可以道里计
好像根本不需要这么复杂的证明。
假设最终可以合并出2^n，那么这一步之前一定是从至少２个2^(n-1)的格子合并出来。我们固定期一个2^(n-1)，那么就只剩下15个格子，要在这15个格子里合出一个2^(n-1)。同理，这必须在14个格子内合出一个2^(n-2)，如此累推。直到最后，要求在1个空格子里出现2^(n-15)，而空格子出现的数字最多是2^2=4。所以n最大可能是17，即最多可能在16个格子合出2^17。