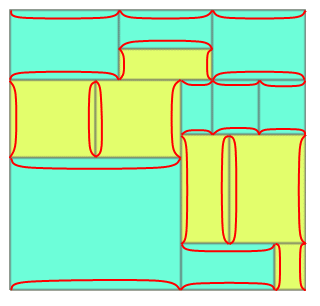
接下来，我们用图论方法来证明：一个由小矩形拼接而成的大矩形，若每个小矩形都有至少一条整数长的边，则大矩形也有至少一条整数长的边。考虑图中每个矩形的每个顶点，把它们作为图G的顶点集（相邻矩形重合的顶点并作一个点）；对于每一个小矩形，把它整数边方向的两对顶点分别用一条边连接起来（相邻矩形公共边上的重边不合并）。如果哪个小矩形四条边都是整数，无妨随意把它当作横向整数边的或者纵向整数边的，连接任一种方向上的边。这样的话，每个矩形恰好产生两条边。注意这个图的一些很显然的性质：度为1的点只有4个（大矩形的四个角），其余的顶点的度都是偶数（只能是2或者4）。下面，我们把这个矩形放在平面坐标系上，大矩形的左下角对齐原点(0,0)。从原点开始沿着图G的边走（每条边最多走一次，不走走过的边），显然走到的每个点都满足这个性质：它的两个坐标均为整数。但我们的出发点是一个度为1的点，在走到另一个度为1的点之前，我们遇到的所有顶点的度都是偶数。因此只要没走到另一个度为1的点，我们就不可能走死。但是，图G总的边数有限，总有一个时候我们将不能再走。因此，这次旅程的终点必然落在另一个度为1的点上。这个终点是大矩形的另一个角，它的两个坐标值均为整数。命题得证。

    以上两个证明均来自http://www.cs.toronto.edu/~mackay/rectangles/

    Andrei Gnepp曾给出一个更简单的证明：显然，一个小矩形的四个顶点中，两个坐标值均为整数的顶点只可能有0个、2个或者4个。把它们全部加起来，符合条件的总顶点数S仍然是偶数。但是，这S个顶点中有些点是重复算过的。假如我们有S1个（两坐标值均为整的）顶点只算过一次，有S2个这样的点被算过两次，有S4个这样的点被加了4次。则有S = S1 + 2*S2 + 4*S4。我们立即得出，S1也是偶数。但我们已经有一个满足条件的点只算过一次（最左下角的点(0,0) ），那么S1至少为2，也即至少还有一个点，它的两个坐标均为整数。它即是大矩形的另一个角。