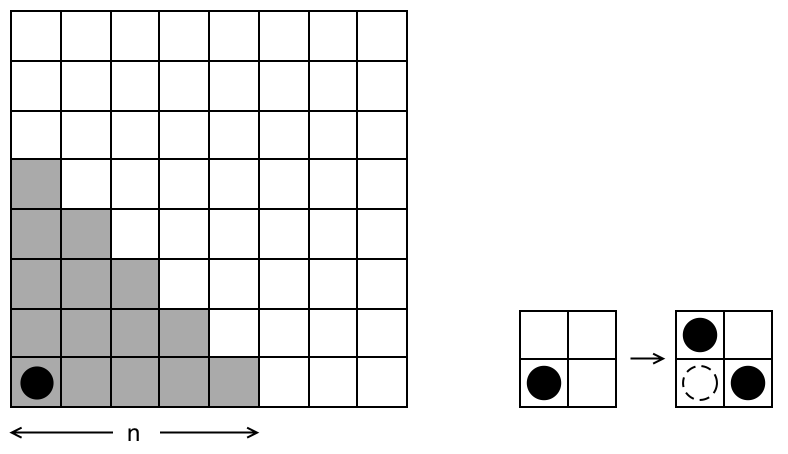
有一个无限大的棋盘，棋盘左下角有一个大小为 n 的阶梯形区域，其中最左下角的那个格子里有一枚棋子，如左图所示。你每次可以把一枚棋子“分裂”成两枚棋子，分别放在原位置的上边一格和右边一格。你的目的是通过有限次的操作，让整个阶梯里不再有任何棋子。下图所示的是 n = 2 时的一种解法。我们的问题是：对于那些 n ，这个游戏是有解的？

 
 
 
 
 
 
 
 
 
 
 
 
 
    当 n = 1 时，第一步直接就解了。刚才我们已经展示了 n = 2 时的解法。不可思议的是，对于其他所有的 n ，这个游戏都是无解的！下面我们就来证明这一点。

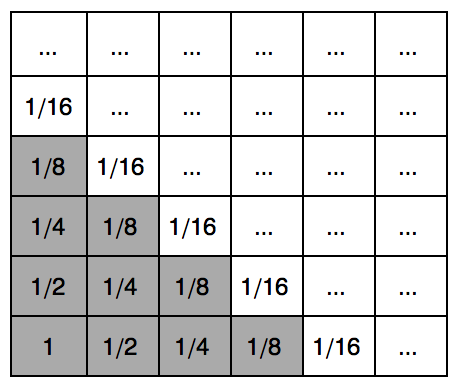
    像上图那样给棋盘中的格子赋值，这样的话，每一步操作都会把棋子从赋值为 x 的格子裂变到两个赋值为 x/2 的格子里，这不会改变所有棋子所在格子的数字之和。因此，所有棋子所在格子的数字之和就是一个不变量，这个值初始时是 1 ，今后则永远都是 1 。接下来，我们能立即得出，所有 n ≥ 4 的情况都是无解的。容易看出第一行所有格子的数字之和是 2 ，第二行所有格子的数字之和是 1 ，接下来几行的数字之和则依次为 1/2, 1/4, 1/8, …，因而整个棋盘上的所有数字之和是 2 + 1 + 1/2 + 1/4 + 1/8 + … = 4 。然而，当 n = 4 时，阶梯区域里的所有数之和为 1 + (1/2) × 2 + (1/4) × 3 + (1/8) × 4 = 13/4 ，空白区域里的所有数之和仅为 4 – 13/4 = 3/4 。因此，我们不可能把所有棋子都移到空白区域里。当然，当 n > 4 时，空白区域里的数字之和会更小，把所有棋子都移到空白区域里就更不可能了。

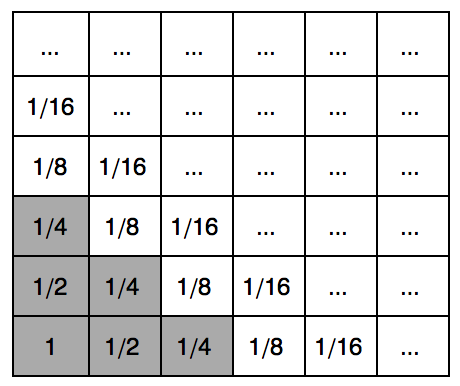
    但是，上面的推理并不能直接适用于 n = 3 时的情况：所有空白区域的数字之和为 4 – 1 – (1/2) × 2 – (1/4) × 3 = 5/4 > 1 ，这么看上去，把所有棋子都移到空白区域似乎是有可能的。然而注意到，不管怎么操作，第一行都只有一枚棋子，第一列也只能有一枚棋子。考虑到这一点，空白区域里的数字之和似乎就又不够了。为了让棋局所对应的数值尽可能地大，最理想的情况便是，第一行的那个棋子正好位于标有 1/8 的格子里，第一列的那个棋子也位于标有 1/8 的格子里，此时第一行和第一列的其他格子都不能再有棋子了，因而我们还得从 5/4 当中减去两个 (1/16 + 1/32 + … ) ，结果等于 5/4 – (1/8) × 2 = 1 。另外，有限次操作不可能让棋子占满中间那片无限大的空白区域，因而棋局可以达到的数字之和严格地小于 1 。如果第一行的那个棋子更靠右，或者第一列的那个棋子更靠上，棋局可以达到的数字之和还会更小。因此，当 n = 3 时，游戏是保证无解的。

    上述游戏是由 Maxim Kontsevich 在 1981 年提出的。有一个类似的跳棋游戏叫做 Conway 的士兵，解决方法也是赋值法，并且更神奇的是，在赋值的过程当中竟然出现了黄金分割 φ 的身影！