2008-07-04 0:02| 
12 Comments | 本文内容遵从 曾经看到过自动扫雷软件，当时我就在想，扫雷游戏是否有什么牛B的多项式算法。最近才看到，扫雷问题居然是一个NP完全问题，并且这个定理有一个简单、直观而又神奇的证明。在这里和大家分享一下整个证明过程。
首先，扫雷一定是NP问题，它显然可以在多项式的时间里验证一个解。接下来，我们需要把一个已知的NP完全问题归约到扫雷问题上去。我们将给出一种把逻辑电路问题归约到扫雷问题的方法，这样的话我们就可以利用扫雷问题解决逻辑电路问题，从而说明逻辑电路问题不比扫雷难。我们将把逻辑电路问题转换成一种对应的扫雷布局，就像画画一样把逻辑电路画在扫雷的棋盘上。如果你还不知道什么叫NP完全问题，什么叫逻辑电路问题，你可以看一看我的这篇文章。
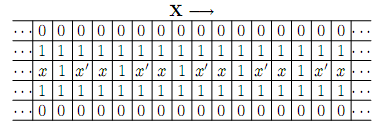
上图就是一条带有Boolean值的线路。注意到x和x'中有且仅有一个有雷。如果（沿线路方向）前一个格子有雷，我们就说这条线路状态为True；反之如果后一个格子有雷，那么这条线路所传递的Boolean值就是False。每条线路的起始端都如下图左所示，其中符号*表示该格里必然有雷，x和x'中同样是有且仅有一个有雷，但到底是哪一个里面有雷谁也说不清楚。线路是可以拐弯的，如下图右所示，这可以保证转角后Boolean值相同。
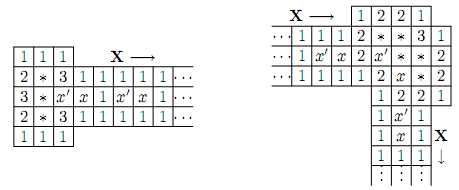
我们需要构造一些特殊的扫雷布局来解释NOT门、AND门和OR门。构造NOT门最为简单，下图就是一个NOT门，注意经过了中间的NOT门后，x和x'的位置互换，True变成了False，False也将变成True。
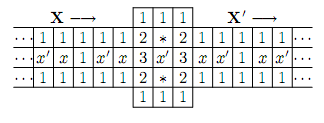
AND门和OR门的构造就比较复杂了。下面是AND门的构造，U和V是输入的两条线路，T是输出的线路。为了说明这确实是一个AND门，我们将说明：在下面的构造中，如果线路T是True（即最右边那个格子t有雷）的话，那么格子u和v必须都有雷才行。如果最右边的格子t有雷，我们可以很快推断出，图中所有其它的t格都是有雷的，所有t'都是无雷的。观察a3正上方的那个"3"，我们立即看出a2,a3都必须有雷，于是继续推得a1无雷，s有雷。类似地，我们可以知道r也是有雷的。在中间一行的*4t处，4的上下左右都已经有雷了，那么u'和v'必然无雷，于是继续往左推得u和v都有雷。
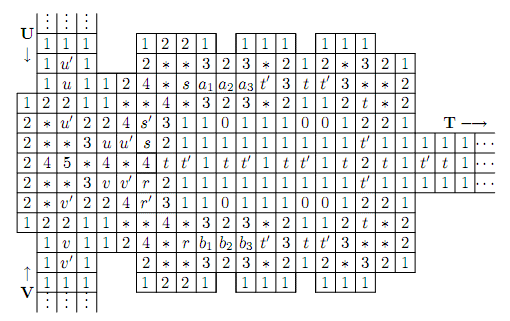
OR门的构造比较类似，如下图。如果r无雷的话，可知a2,a3有雷，a1无雷，s'有雷，进而s无雷。观察"6"可知u'和v'都有雷，于是u和v均无雷。
不断套用这几个逻辑门的构造图来连接电路，直到输出线路只剩下唯一的一条。把最后的输出线路从x或者x'处截断（相当于把最终输出的Boolean值定下来）后，整个布局就成了一个“扫雷版SAT问题”了。
最后还有一个容易忽略的问题：要是线路交叉了该咋办？下图的构造可以保证线路交叉后仍不改变原线路所带的Boolean值。至此，我们已经可以把任一逻辑电路布局到扫雷棋盘上，解决这个扫雷问题就相当于要解一个逻辑电路问题，因此扫雷问题至少和逻辑电路问题一样难。
沙发…
很早以前就知道这个结论了～
呃，什么是扫雷问题呢？
从文中来看，扫雷问题似乎是“给定一个地图的初始状态，求满足这个初始状态的一个解”？
以前我还打算过编一个自动解扫雷的程序，没想到竟然是NPC
在http://zhiqiang.org/blog/上见过
我们需要把一个已知的NP完全问题规约到扫雷问题上去。
“规约”是不是应该是“归约”
PS:麻烦Matrix67牛再指点我DROD LV12关，我在和一个分身破蓝色怪物时卡住了，就是你要左边走一下，右边走一下，我先第一次向右走时卡住了……
回复：谢谢指正，已经改了
你说的是1E房间？把怪物引到箭头上，分身就踩不进去了
好……好……好简单的证明-.-~~~
太……强了，我完全拜倒在您的智慧之下了……
编写自动扫雷的软件可以先读取软件的数据,然后再用软件控制扫雷,不用自己求雷的位置.
楼层: 地幔 | 2008-7-06 22:42 | 阿健 说：
编写自动扫雷的软件可以先读取软件的数据,然后再用软件控制扫雷,不用自己求雷的位置.
=========================================
喂喂喂我们在讨论算法算法～不是这种技巧～
厉害
不错。不过有一点，这里minesweeper实际上是由planar-3-sat而不是一般的3-sat归约过去的。由这个问题建立归约也是证明平面几何问题np-completeness的常用思路。
"下图的构造可以保证线路交叉后仍不改变原线路所带的Boolean值"
没看到这句，是我想当然了。