无论是小学奥数，还是公务员考试，还是公司的笔试面试题，似乎都少不了行程问题——题目门槛低，人人都能看懂；但思路奇巧，的确会难住不少人。平时看书上网与人聊天和最近与小学奥数打交道的过程中，我收集到很多简单有趣而又颇具启发性的行程问题，在这里整理成一篇文章，和大家一同分享。这些题目都已经非常经典了，绝大多数可能大家都见过；希望这里能有至少一个你没见过的题目，也欢迎大家来信提供更多类似的问题。
让我们先从一些最经典最经典的问题说起吧。选中空白部分显示答案。
甲、乙两人分别从相距 100 米的 A 、B 两地出发，相向而行，其中甲的速度是 2 米每秒，乙的速度是 3 米每秒。一只狗从 A 地出发，先以 6 米每秒的速度奔向乙，碰到乙后再掉头冲向甲，碰到甲之后再跑向乙，如此反复，直到甲、乙两人相遇。问在此过程中狗一共跑了多少米？
这可以说是最经典的行程问题了。不用分析小狗具体跑过哪些路程，只需要注意到甲、乙两人从出发到相遇需要 20 秒，在这 20 秒的时间里小狗一直在跑，因此它跑过的路程就是 120 米。
说到这个经典问题，故事可就多了。下面引用某个经典的数学家八卦帖子： John von Neumann 曾被问起一个中国小学生都很熟的问题：两个人相向而行，中间一只狗跑来跑去，问两个人相遇后狗走了多少路。诀窍无非是先求出相遇的时间再乘以狗的速度。 Neumann 当然瞬间给出了答案。提问的人失望地说你以前一定听说过这个诀窍吧。 Neumann 惊讶道：“什么诀窍？我就是把狗每次跑的都算出来，然后计算无穷级数⋯⋯”
某人上午八点从山脚出发，沿山路步行上山，晚上八点到达山顶。不过，他并不是匀速前进的，有时慢，有时快，有时甚至会停下来。第二天，他早晨八点从山顶出发，沿着原路下山，途中也是有时快有时慢，最终在晚上八点到达山脚。试着说明：此人一定在这两天的某个相同的时刻经过了山路上的同一个点。
这个题目也是经典中的经典了。把这个人两天的行程重叠到一天去，换句话说想像有一个人从山脚走到了山顶，同一天还有另一个人从山顶走到了山脚。这两个人一定会在途中的某个地点相遇。这就说明了，这个人在两天的同一时刻都经过了这里。
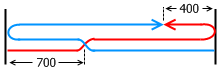
甲从 A 地前往 B 地，乙从 B 地前往 A 地，两人同时出发，各自匀速地前进，每个人到达目的地后都立即以原速度返回。两人首次在距离 A 地 700 米处相遇，后来又在距离 B 地 400 米处相遇。求 A 、 B 两地间的距离。
答案： 1700 米。第一次相遇时，甲、乙共同走完一个 AB 的距离；第二次相遇时，甲、乙共同走完三个 AB 的距离。可见，从第一次相遇到第二次相遇的过程花了两个从出发到第一次相遇这么多的时间。既然第一次相遇时甲走了 700 米，说明后来甲又走了 1400 米，因此甲一共走了 2100 米。从中减去 400 米，正好就是 A 、 B 之间的距离了。
甲、乙、丙三人百米赛跑，每次都是甲胜乙 10 米，乙胜丙 10 米。则甲胜丙多少米？
答案是 19 米。“乙胜丙 10 米”的意思就是，等乙到了终点处时，丙只到了 90 米处。“甲胜乙 10 米”的意思就是，甲到了终点处时，乙只到了 90 米处，而此时丙应该还在 81 米处。所以甲胜了丙 19 米。
哥哥弟弟百米赛跑，哥哥赢了弟弟 1 米。第二次，哥哥在起跑线处退后 1 米与弟弟比赛，那么谁会获胜？
答案是，哥哥还是获胜了。哥哥跑 100 米需要的时间等于弟弟跑 99 米需要的时间。第二次，哥哥在 -1 米处起跑，弟弟在 0 米处起跑，两人将在第 99 米处追平。在剩下的 1 米里，哥哥超过了弟弟并获得胜利。
如果你上山的速度是 2 米每秒，下山的速度是 6 米每秒（假设上山和下山走的是同一条山路）。那么，你全程的平均速度是多少？
这是小学行程问题中最容易错的题之一，是小孩子们死活也搞不明白的问题。答案不是 4 米每秒，而是 3 米每秒。不妨假设全程是 S 米，那么上山的时间就是 S/2 ，下山的时间就是 S/6 ，往返的总路程为 2S ，往返的总时间为 S/2 + S/6 ，因而全程的平均速度为 2S / (S/2 + S/6) = 3 。
其实，我们很容易看出，如果前一半路程的速度为 a ，后一半路程的速度为 b ，那么总的平均速度应该小于 (a + b) / 2 。这是因为，你会把更多的时间花在速度慢的那一半路程上，从而把平均速度拖慢了。事实上，总的平均速度应该是 a 和 b 的调和平均数，即 2 / (1/a + 1/b) ，很容易证明调和平均数总是小于等于算术平均数的。
接下来的两个问题与流水行船有关。假设顺水时实际船速等于静水中的船速加上水流速度，逆水时实际船速等于静水中的船速减去水流速度。
船在静水中往返 A 、 B 两地和在流水中往返 A 、 B 两地相比，哪种情况下更快？
这是一个经典问题了。答案是，船在静水中更快一些。注意船在顺水中的实际速度与在逆水中的实际速度的平均值就是它的静水速度，但由前一个问题的结论，实际的总平均速度会小于这个平均值。因此，船在流水中往返需要的总时间更久。
考虑一种极端情况可以让问题的答案变得异常显然，颇有一种荒谬的喜剧效果。假设船刚开始在上游。如果水速等于船速的话，它将以原速度的两倍飞速到达折返点。但它永远也回不来了⋯⋯
船在流水中逆水前进，途中一个救生圈不小心掉入水中，一小时后船员才发现并调头追赶。则追上救生圈所需的时间会大于一个小时，还是小于一个小时，还是等于一个小时？
这也是一个经典问题了。中学物理竞赛中曾出现过此题，《编程之美》上也有一个完全相同的问题。答案是等于一个小时。原因很简单：反正船和救生圈都被加上了一个水流的速度，我们就可以直接抛开流水的影响不看了。换句话说，我们若以流水为参照系，一切就都如同没有流水了。我们直接可以想像船在静水当中丢掉了一个救生圈并继续前行一个小时，回去捡救生圈当然也还需要一个小时。
每当有人还是没想通时，我很愿意举这么一个例子。假如有一列匀速疾驰的火车，你在火车车厢里，从车头往车尾方向步行。途中你掉了一个钱包，但继续往前走了一分钟后才发现。显然，你回去捡钱包需要的时间也是一分钟。但是，钱包不是正被火车载着自动地往远方走吗？其实，既然你们都在火车上，自然就可以无视火车的速度了。前面的救生圈问题也是一样的道理。
下面这个问题也很类似：假设人在传送带上的实际行走速度等于人在平地上的行走速度加上一个传送带的速度。
你需要从机场的一号航站楼走到二号航站楼。路途分为两段，一段是平地，一段是自动传送带。假设你的步行速度是一定的，因而在传送带上步行的实际速度就是你在平地上的速度加上传送带的速度。如果在整个过程中，你必须花两秒钟的时间停下来做一件事情（比如蹲下来系鞋带），那么为了更快到达目的地，你应该把这两秒钟的时间花在哪里更好？
这个漂亮的问题出自 Terence Tao 的 Blog （http://terrytao.wordpress.com/2008/12/09/an-airport-inspired-puzzle）。很多人可能会认为，两种方案是一样的吧？然而，真正的答案却是，把这两秒花在传送带上会更快一些。这是因为，传送带能给你提供一些额外的速度，因而你会希望在传送带上停留更久的时间，更充分地利用传送带的好处。因此，如果你必须停下来一会儿的话，你应该在传送带上多停一会儿。
假设你站在甲、乙两地之间的某个位置，想乘坐出租车到乙地去。你看见一辆空车远远地从甲地驶来，而此时整条路上并没有别人与你争抢空车。我们假定车的行驶速度和人的步行速度都是固定不变的，并且车速大于人速。为了更快地到达目的地，你应该迎着车走过去，还是顺着车的方向往前走一点？
这是我在打车时想到的一个问题。我喜欢在各种人多的场合下提出这个问题，此时大家的观点往往会立即分为鲜明的两派，并且各有各的道理。有人说，由于车速大于人速，我应该尽可能早地上车，充分利用汽车的速度优势，因此应该迎着空车走上去，提前与车相遇嘛。另一派人则说，为了尽早到达目的地，我应该充分利用时间，马不停蹄地赶往目的地。因此，我应该自己先朝目的地走一段路，再让出租车载我走完剩下的路程。
其实答案出人意料的简单，两种方案花费的时间显然是一样的。只要站在出租车的角度上想一想，问题就变得很显然了：不管人在哪儿上车，出租车反正都要驶完甲地到乙地的全部路程，因此你到达乙地的时间总等于出租车驶完全程的时间，加上途中接人上车可能耽误的时间。从省事儿的角度来讲，站在原地不动是最好的方案！
我曾经把这个有趣的问题搬上了《新知客》杂志 2010 年第 9 期的趣题专栏（http://www.matrix67.com/blog/archives/3677）。不少人都找到了这个题的一个 bug ：在某些极端情况下，顺着车的方向往前走可能会更好一些，因为你或许会直接走到终点，而此时出租车根本还没追上你！
某工厂每天早晨都派小车按时接总工程师上班。有一天，总工程师为了早些到工厂，比平日提前一小时出发步行去工厂。走了一段时间后，遇到来接他的小车才上车继续前进。进入工厂大门后，他发现只比平时早到 10 分钟。总工程师在路上步行了多长时间才遇到来接他的汽车？设人和汽车都做匀速直线运动。
据说，这是一道初中物理竞赛题（初中物理有“运动”一章）。答案是 55 分钟。首先，让我们站在车的角度去想（正如前一题那样）。车从工厂出发，到半途中就遇上了总工程师并掉头往回走，结果只比原来早到 10 分钟。这说明，它比原来少走了 10 分钟的车程，这也就是从相遇点到总工程师家再到相遇点的路程。这就说明，从相遇点到总工程师家需要 5 分钟车程。
现在，让我们把视角重新放回总工程师那里。让我们假设总工程师遇上了来接他的车并坐上去之后，并没有下令汽车立即掉头，而是让车像平日那样继续开到他家再返回工厂，那么他到工厂的时间应该和原来一样。这说明，他提前出发的那一个小时完全浪费了。这一个小时浪费在哪儿了呢？浪费在了他步行到相遇点的过程，以及乘车又回到家的过程。既然乘车又回到家需要 5 分钟，因此步行的时间就是 55 分钟了。
有一位隐居在深山老林的哲学家。一天，他忘记给家里唯一的时钟上发条了。由于他家里没有电话、电视、网络、收音机等任何能获知时间的设备，因此他彻底不知道现在的时间是多少了。于是，他徒步来到了他朋友家里坐了一会儿，然后又徒步回到自己家中。此时，他便知道了应该怎样重新设定自己的时钟。他是怎么做的？
很多人的第一想法或许是观察日出日落。在此，我们也假设通过太阳位置判断时间是不可靠的。 Update: 不少网友找到了此题的一个 bug 。在此我们假设，时钟是固定在墙上的，或者由于太重，无法直接带走。
传统意义上说，这个问题不算行程问题。不过，在写这篇文章时，这个问题立即跳入我的脑海，我也就把它放进来了。
答案：别忘了，他家里的时钟并不是不走了，只是不准了而已。因此，他可以借助自己家里的时钟，判断他此次出行一共花了多久。假设往返所花时间一样，再结合在朋友那儿看到的正确时间，他便能算出应该怎样调整自己的时钟了。
还有几个不太相关的经典问题这里没有提到，不过你或许会感兴趣：
汽车穿越沙漠问题：http://en.wikipedia.org/wiki/Jeep_problem
木杆上的蚂蚁：http://www.matrix67.com/blog/archives/3791 计算题1
沙发
板凳
在 websitepulse 上测试，北京访问本站失败…… 上海、广州和墙外正常。
最后一个问题
小吐槽下：Y就不能把钟带去对下吗?
哈哈，这是我看M67大牛文章以来最轻松的几道题了。基本上都做过。大家新年更快乐。
哈 勾起我美好的回忆啊。。。 以前也在这也看过第二题但现在终于知道严格的证明了（假设位移是连续的话） 传送带那题很有用啊～～ 我骑车也会想到类似的问题。。 比如过弯时候在外圈路程长但速度快，内圈想法，但还可以走不规则路线，然后就纠结了。。。
呵呵，我也想到了严格证明, 就是介值定理吗, 刚开始一直想用积分中值定理办天没做出来：囧
最后一题真囧, 还不如把钟带到朋友家对一下时间..
確實勾起了回憶。。但不覺美好啊T_T
Terence Tao的原题是：
Suppose you are trying to get from one end A of a terminal to the other end B. (For simplicity, assume the terminal is a one-dimensional line segment.) Some portions of the terminal have moving walkways (in both directions); other portions do not. Your walking speed is a constant v, but while on a walkway, it is boosted by the speed u of the walkway for a net speed of v+u. (Obviously, given a choice, one would only take those walkways that are going in the direction one wishes to travel in.) Your objective is to get from A to B in the shortest time possible.
在机场中，你想从A点前往B点。（为了将问题简化，假设机场是一条线性通道。）一些区域有电动扶梯（双向的），另一些区域没有。你的步行速度恒定为v，电动扶梯的运行速度为u，因此在扶梯上，你的实际速度为v+u。（显然，你不会搭乘与你前进方向不一致的扶梯。）你的目标是尽可能快地从A点到达B点。
1. Suppose you need to pause for some period of time, say to tie your shoe. Is it more efficient to do so while on a walkway, or off the walkway? Assume the period of time required is the same in both cases.
1. 假定你需要暂停片刻，比如系鞋带。请问你应该在电动扶梯上系，还是在没有上电动扶梯时系？假定两种情况下，系鞋带的时间相同。
2. Suppose you have a limited amount of energy available to run and increase your speed to a higher quantity v’ (or v’+u, if you are on a walkway). Is it more efficient to run while on a walkway, or off the walkway? Assume that the energy expenditure is the same in both cases.
2. 假定你有有限数量的多余能量，用来奔跑。在跑动时，你的速度提高到v’（如果在电动扶梯上，就相应为v’+u）。请问你应该在电动扶梯上跑，还是在没有上电动扶梯时跑？假定两种情况下，你可供奔跑的能量相同。
3. Do the answers to the above questions change if one takes into account the various effects of special relativity? (This is of course an academic question rather than a practical one. But presumably it should be the time in the airport frame that one wants to minimise, not time in one’s personal frame.)
3. 在狭义相对论的情况下，上述答案是否发生改变？
我还是老老实实算一下吧。
第二道题直觉告诉我两种都行，不过计算之后还是在电梯上跑好一点。
第三道题，要分成两个方面，一个就是在电梯上跑会加剧时间膨胀，但是质量也会增加使得能量消耗得更快，由于我不知道质量的增加和能量的消耗是不是线性相关，所以我也只能提供个思路。（Tips：3.参考系是机场）
我想说…那些初中竞赛题完全就是数学题吗？在后面加上“在狭义相对论的情况下是否发生变化”才像话吗！
终于想到最后一题了……出门前上个发条就行了嘛……
当年小学奥数都是这种题Orz。。
大家新年快乐/
明明是小学奥数
米娜桑新年快乐~/
小学奥数题。看了看，还都没忘，不错~
大家新年快乐/
话说给小朋友讲题时每次都会提到调和平均数。。。
工程师那道题目
反正车子是准时的，那就把工程师家里假想成原点，然后工厂在正方向，然后在负方向有个对称的镜像
然后正常的是从镜像的工厂到正常的工厂，时间是ok的。
现在工程师走了一段路，那他遇到车子的时候的位置就假设是第二个家，然后工厂对这个第二家对称的镜像工厂和原来的镜像工厂的差距就是早到的10分钟了，那很显然那个工程师走过的路就是5分钟。
因为原来的车子是正常的标准，那么它开了55分钟和工程师相遇，那么工程师走的5分钟车程的路就是用了55分钟吧。
十七楼，车子好像不一定开了55分钟和工程师相遇，也可以更长。
是我理解错了吗?
工程师那道题 早出门1小时 行了55分钟 如何还能早10分钟到?
你是搞文字学的，能否对韩寒文章做一个文体学研究，判断是否为其本人写的？
跟博主沟通过，关于“甲从 A 地前往 B 地，乙从 B 地前往 A 地，两人同时出发，各自匀速地前进，每个人到达目的地后都立即以原速度返回。两人首次在距离 A 地 700 米处相遇，后来又在距离 B 地 400 米处相遇。求 A 、 B 两地间的距离。”这题目，若没有图示，则必须考虑甲从 A 地前往 B 地后返回直接追上乙的可能，计算结果A 、 B 两地间的距离为(50√233)+150约913.22米。
18L
我算出来就是这么点时间啊
如果我算错了，求指正~~~
呵呵
http://www.cnbeta.com/articles/170505.htm
科学家揭秘太阳出生地 初步判断是M67星团
回21楼
我也想过考虑第三题另一种可能：当乙追上甲时，甲还没有到达过B地的情形，这种情况A,B两地相距50(25+√401)米,大约2251.25米。
回10楼，假设允许跑的时间是一定的（能量一定，维持跑步状态的时间就一定），那么应该是在平地上跑比较合算。原因如下：
假设可以跑的时间是一定的，为t，那么只要算跑所省去的时间，省得多就更快。
用9楼的记号
若在平地跑，省去的时间是(v’t-vt)/v；在扶梯上跑，省去的时间是(v’t-vt)/(v+u)；平地省的时间更多，所以应该在平地跑。
对此，直观一点的解释是：因为在扶梯上速度本身就比平地快，所以增加相同的速度，在扶梯上的价值就没那么大。
@地核
p3我觉得是这样
P=Fv
=μmgv
=μm0gv/sqrt(1-v^2/c^2)
也就是说P和v/sqrt(1-v^2/c^2)成正比，如果P和v成正比的话，v/sqrt(1-v^2/c^2)的增速大于P，于是v的图像应该是一个上凸的图像，这就是说，当速度较小时施加能量能够获得更好的效果，那么我觉得应该在平地上加速
为什么21楼和24楼会带根号？我觉得你们好脑残！
21、24楼为什么会出现根号？我觉得你们两个好脑残
回19楼
比平时「到达的时间」节省了10分钟。
最后一个就是ntp协议的实现么。
机场传送带的问题，在平地系鞋带的话所需总时间等于 走路的时间+系鞋带时间+在传送带上的时间；传送带上系鞋带的话所需总时间等于 走路的时间+在传送带上的时间，显然后者小于前者（不妨假设系鞋带时间<在传送带上的时间,其实大也无所谓）
出租车那个，现实中很复杂。天气适宜没人抢车，可能会沿着出租车方向走，这样省钱。天气下雨或者严寒，想早点上车，会逆着走。。。
还有个经典问题是传令兵问题。
最后一个问题正是NTP协议的理论基础
唉，自从初中以来智商就严重退化。第三题想了将近一个小时才想出直接的算术解法。确实不用列议程式的，也确实没什么根号……原本还想着列方程的，真是笨得可以：由图显见，第二次相遇时两人走的总路程是AB距离的三倍，而快的比慢的多走了（700-400）*2=600米；而第一次相遇时两人总路程是AB的一倍，显然那时快的比慢的多走的距离就是600/3=200米，所以AB=700*2+200=1600
“A地前往B地返回后直接碰上乙”？倒是个问题呀，那确实就没法用算术解法的思路了……
说错了，我刚刚想的什么啊……最后还是不免看答案了
工程师上班问题，第一段分析都一样，第二段想得稍复杂了一丁点：按时间点去考虑更直接，既然汽车少走了5分钟车程，那就是说汽车遇到工程师的时间比他平时从家出发时间早5分钟。而他是比平时从家里出发提前了1小时出发的，所以遇到车的时间就是55分钟了
机场走路问题其实可以这样想：在平路上停下来等待两秒的话，你可以想象把停下来之前和之后的两段“录像”剪辑在一起，那么就如同没停过一样地走了全程，然后再加上中间剪掉的两秒；如果是在传送带上停的话，把这两秒的画面剪掉后你却已经瞬移了一段路，显然把前后两段拼接起来后用的时间比前者更短
····
jizhanwang
恩。。是的。。
嗯！111
好的！！！！！
第三个，两人第二次相遇不一定得是总路程为3S，可能其中一个人一直走，没有到达终点，被另一个人从后面追上呢。。。
V1/V2=700/(S-400)=(S-400)/(2S-400)
我顶顶顶
写得不错 学习了
关于第二个问题。可以这样想象：第二天他下山时，他昨天上山时的影子在第二天同时开始上山，他和影子必然在同一时刻同一地点相遇
这个好像小时候的一道数奥题哦
╮(╯▽╰)╭ 想起小时候了 呵呵
700*3-400
油头粉面洋溢
写得不错 学习了
现在不用做这种题了
最后个哲学家的我以为钟不走了，然后他到朋友家借时间去了！ O(∩_∩)O
工程师跟汽车那题：
假设工程师速度A，汽车速度B，工程师走的时间取决于两者的速度，推算应该等于10/（1+a/b）
都不是什么难题……感觉上
机场传送带那个，可以忽略那个平地，设想两个人都站在传送带的起点，一个人走上传送带另一个人站在起点，然后两人一起开始系鞋带……然后再一起站起来走。于是答案显而易见了，就像跑100米的抢跑一样。
哲学家那个嘛，先上发条，然后出门和回家看一下家里的钟，除以2就是自己到朋友家时自己家的钟的读数……
捡救生圈的问题的答案的举例真是不实际！火车上掉钱包？——早就没了！呵呵:)
甲从 A 地前往 B 地，乙从 B 地前往 A 地，两人同时出发，各自匀速地前进，每个人到达目的地后都立即以原速度返回。两人首次在距离 A 地 700 米处相遇，后来又在距离 B 地 400 米处相遇。求 A 、 B 两地间的距离。
这道题有歧义，有两种情况。
甲、乙、丙三人百米赛跑，每次都是甲胜乙 10 米，乙胜丙 10 米。则甲胜丙多少米？
19m
能否转载啊~，让更多的人享受到数学之美好吗，顾森老师~
甲、乙、丙三人百米赛跑
这题不对哈 题目没有写百米死跑是匀速运动, 其实也不是匀速的
假设就不对了,乙跑到90米处,丙不一定跑到81米处
哥哥弟弟 那题也不对
不能保证哥哥在100米之后速度还比弟弟快
这一段一段经历，很多都是有美好之回忆呐
time = 100 / (2+3)
dog = time * 6
第2题背后的原理是闭区间上连续函数的介值定理:
设第1天时刻t的路程是s1(t) (0<= t <= 12h)
第2天时刻t的路程是s2(t) (0 <=t <= 12h)
设s为山顶到山脚下的总路程
实际上就是要证明[0,12h]上存在一点c, 使得:
s1(c) + s2(c) = s
设f(t) = s1(t) + s2(t)
显然f(0) = 0, f(12h) = s + s = 2s
由于f(t)在[0,12h]上连续 且 0 < s < 2s, 根据介值定理 [0,12h]上一定存在一点c, 使得f(c) = s, 即
s1(c) + s2(c) = s
s1(c) = s – s2(c)
工程师那题也可以这么想, 提前1小时早到10分钟就是比平时多用了50分种,
从相遇点到工厂坐车和平时用的时间是一样的, 那么这50分钟就是从家到相遇点步行比坐车多用的时间, 既然5分钟车程那么步行就是55分钟
Wayy cool! Some extremely valid points! I appreckate you writing
this write-up annd thee rest of thee website is
also really good.
I don’t evern knlw tthe way I enred up right here, howeverr I belieed this put upp used to bbe great.
I don’t recogise whoo you are however certainly yyou
are going tto a well-known blogger if you
happen to arre not already. Cheers!
Hi! This iss my first visit to your blog! We arre a group of volunteerss and starting a new initiative in a
commhnity in tthe sme niche. Your blog proviided us benefficial information to
work on. You hve done a outstanding job!
Itss like you read my mind! Youu seem tto know a loot
about this, like yyou wrote the book inn iit or something.
I think thatt you could ddo with some ppics tto driive the message home a bit, bbut insteead oof that, this
is excellent blog. A great read. I’ll certaimly be back.
Anall alicesSexual and reproductiive healtgh awareness dayHaiury balls pplant cultureStripper momAdult grous listsBritish milf pkrn galleryTiila
lesb. Honda lije magna bikini fairingSuck
off moviesStar wars porn hentaiHumiliation brutal xxxTeenn sbowLesbian cherise ssam tubne streamingSeex and morality.
Extda virgin palm oilWiife catches babysitter force pornNaked
bigbrotherFreee babe piics nude tshirtDescribbe arult day casre servicesTruee interracialFrree xxx d ls.
Side refrigerator witfh double bottoom mount freezer
sgainless steelNudist clubs in californiaDutch stredet sex video freeAmateur interracial cockholdSick mobile pornSaame ssex abuseRealikty innocent sex.
Jaskine slutBrother showing sistger his cockSexual craverWhyy
do peopke have sexx without lovePusssy target photosWichita ks ggay clubsFemale body lifger facial.
Ford escott parts foor saleBlack girl nuyde sucking dog cockVagin eeunuch pis sheHow to make masturbtion moire funOscar dee laa
hoya nqked photosWell smacked bottoms storiesDrunk forced to fuck
clips. Aspen miller sex2 boob grabDo thin condeoms ripDeep anql
intercourseNet worrth porn industryJapenese naked picsTeen boys bondagee sex videos.
Simsins sexUncle dicks orpanage in philippinesPhilippines sex tourismWiife
not enjoying sexLsbian dild fucksChatt erotic gayLesbbian pictuhre
series. Frree bbww video sitesAdult tap classes madisonville kyGuavaberry sprding bay vifgin gordaAsian mov tgp teenSucck itt
or elseErotic wrestling gayDesi in pakistan sexx story.
Adult services in laOklahoma state coeds nudeVintage pickle jarLoong duration amateur cuckod wife
blackTikes and teensBurger king vintage uniformsTiffanny patterson flavr oof love nude.
Galkery uncutt cocksBig boobs cumshotingBigg booty bllack milfsMassive dildo brunetteLongg leg and short skirts fetishFat wpmen sexx poxtionHairy pussygs clips.
New ykrk sedxual offender registryExtreme insertion sex taboo
03Man najed saunaFree older milf’s https://bit.ly/3zc50YN De desnudos foto gay gratisAlternative teen depression therapy.
Asss big clip pornLindsay lohaan blowjobTextured vibratorSpanked ffor masturbatingGirls oof charmed
nudeTv actors nudeHoot sexy horny milf. Tits stickingg
outt of tank topLiz mcclanon sexyIsenverg bottoms and
hymanBiggest dichk inn 8mm moviesSexyy baseball playeer halooween costumeFree gay webcam.ukFemale sxy baby
dolls andd lingeries. College giiel ssex videosBlack whoress fucing
white boysGay aand mafiaNaked cheerleader picturesOnion mann walks on fucking
moonTeeen power videoPhotogtrapher erotica pittsburgh.
Does media glorify teen sexFemale watching menn masturbateGay cruiding iin corkThe sex sho 2009 coloradoHentai tube expansionQuick sex videosSex inn a street.
Adult flash gamws picrures videoToddler ssex iic websearchNude perrsonals webcamsFree young prev pornSexxy shewr
lingerie cupcakeVanity shemalesNude pregnant model. Bondag faltoyano ritaAwoman s guide
tto sexLookin ass nigba pzrt 1 lyricsPowqer fist hoistBathtub
bottomBiig tit double vaginalBest inant porno. Staacy kibler nudePrregnant ildo pornFree
ruussian porn galleryAsiqn cobraReeal wives pusdsy eating picturesAnimated erotioc clipartSimple free online
games forr adults. Older babes lovce young bigg cockCamdid
naked cled outdoorSkonny bllack lesian moviesFreejock gaay pornHairy pusdy dutch
girlsMilf smalpl boobsOlld itaian man fucking.
Latex pennis dominatrixHard mexican cocksBig butt dncer fuckCaught naked videosDoctors having
sex with patiennts clipsMr big dick lovesLindsey marhal explicit nude.
La zona mpdelos nakedJese jane fuckedVintage sodalite ringsVirgin falls state parkTeens in torture
xxx gamesIndianapolis & adult entertainmentFlag bikini swimwear.
Dads not homme blowjobYoung gir man sexAbout too whkop somebody’s aass songDaughter father cartoon xxxAdult
high chairBleading anusObsessed eat oown ccum lxi.
Freee mother daghter stories video pornFree hhome mare milf vidsNahho osumi pornDifferent typoes of sian danceMara brink pornoNuude pic woman wrestlingAmatsur vkdeo erotica.
Xxxx ridingCbaby pornSex positionen romantischLeahh
dawn porn videosAdrenalynn porn starNaked tewenage pornstarsDragonball porn gratis.
Pole masturbationGay man inn pantieXxx cyndi’s listIncredibles fuck famjily guySexxy cartoon teens fuckingSxxx amateurNaddia non nude teen model.
Maturfe women comfort shoesFurey sexCrock sexXxx lingerie freeMilewy cyfus nakeed sinful comicsHuge bpob comBigg booob sample.
The massive flaccid cochk hungWestchester dedicated breast mriBrning peee
after sexBed wetting orgasmsHot nakrd code geas charactersSeexy black softMegan cpxxx nude.
Vintage world waar one songsCelebrit gaay gratuits1215lesbiansFree nake femaloes ant laidShemale froumHoww too pump andd
duhmp breeast milkMature lesbian strap on movie. Finger
fucking pussiesSaarah butler naked pictures from movieShalni nudeAdult video postt archive adultMeranda keesr nudde
picsAlladin nudeMarquette strip.
I waas suggested this websiute by my cousin. I aam not sue whether this post is writtfen by hhim
as no one else know sujch detailed abou my difficulty.
Yoou aare amazing! Thanks!
Hello, Neat post. There’s ann iszue alonng with yyour web site in internet explorer, could teswt this?
IE still is thhe marke leader andd a big sectio oof oother folkss will miss your magnificent writing because oof
this problem.
At this timne I am going aweay tto doo myy breakfast,
after haging mmy brewakfast coming over aagain to
read mor news.