情人节特献：有心之函数必然就有分手函数

    首先，祝大家情人节快乐。不过，对于单身 Geek 来说，情人节或许并不快乐。情人节可以说是各种 Geek 们永久的伤痛了。即使是热爱数学的你，或许看到已经被转发到烂的“心之函数”今日再度走红，心中也会觉得不爽：我们发明出来的 Geek 玩物，竟然都被你们这些非 Geek 人士拿去装 Geek 泡妞用了，最终情人节宅在家里面向显示器编程度过平凡一天的反而还是我们这群 Geek 。

  

    于是乎，“订完全部大床房”、“买光影院单号位”、“扎破所有安全套”等经典段子年年少不了。当然，我也没有闲着。为什么有 Geek 式的爱情祝福，就没有 Geek 式的分手诅咒？我计划着创作一个“分手函数”，它的函数图像是一个裂成两半的心。


    要制造分手函数，首先要有一个等待被恶搞的心形原型。我所选用的原型函数则是 2006 年 5 月 4 日本 Blog 所发文章里的函数（看到五年前的文章真是让我感慨万千啊）。这个函数的形式相当对称美观： 17 x^2 – 16|x|y + 17 y^2 < 225 。用 Mathematica 画出来大概是这样：   

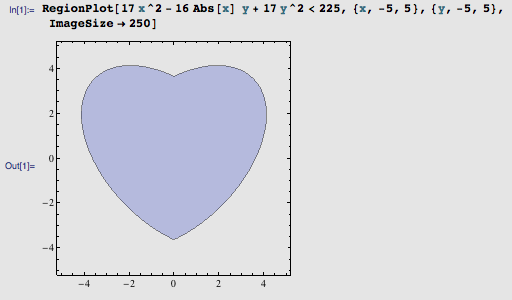
    这个心形函数的成因非常简单，去掉中间一项的绝对值后你就明白了：

  

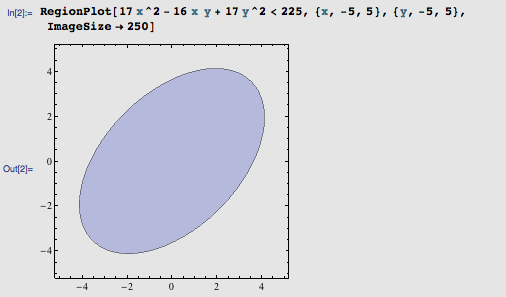
    原来，17 x^2 – 16 x y + 17 y^2 < 225 将会画出一个椭圆，因此给 x 加上绝对值，相当于把平面直角坐标系 y 轴右半部分镜像过来，就得到一个大致的心形了。我们的目标，便是要沿着 y 轴方向给这颗心加上一道的裂缝。     裂缝一般都是锯齿形的。什么函数也是锯齿形的呢？最常用的估计就是三角函数和取余函数了吧。这里，我决定用大家熟知的并且也是相对容易控制的正弦函数来描绘裂缝的形状。考虑二元函数 f(x, y) = x ，由于所有 x 坐标相同的点函数值都一样，它的“等高线图像”就是一条条简单的竖直线，如图所示：   

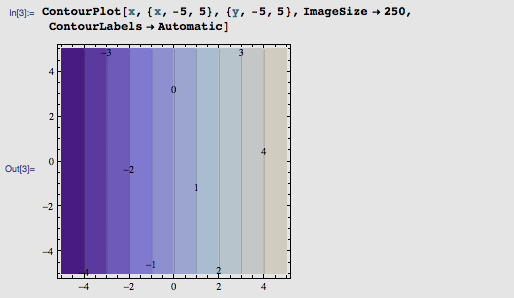
    那么，函数 f(x, y) = x + sin(y) 就是对上图中纵坐标为 y 的所有点偏移 sin(y) 的量，也就把一个个带状区域扭成了波浪。

  

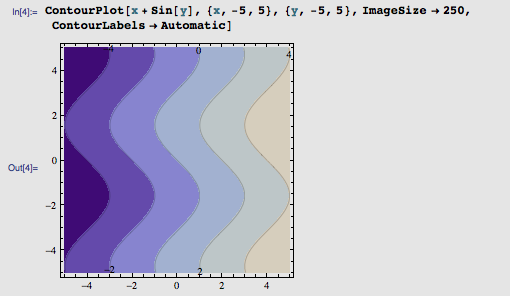
    不过，这个波浪似乎还不够剧烈，离我们的“裂缝”要求远了些。我们不妨加大正弦函数的频率：

  

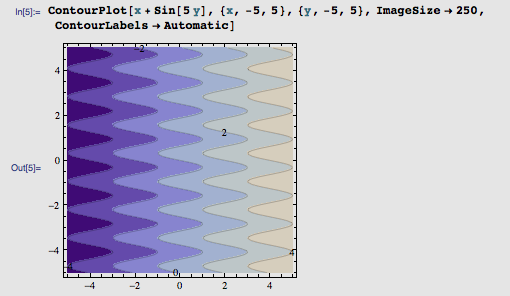
    哇， f(x, y) = x + sin(5 y) 的周期倒是变短了，不过这波动得也太剧烈了一些。看来，我们应该让 x 的变化也稍微剧烈一些，让它能适应 sin(5 y) 的步伐。于是，我把 f(x, y) 改成了 5 x + sin(5 y)

  

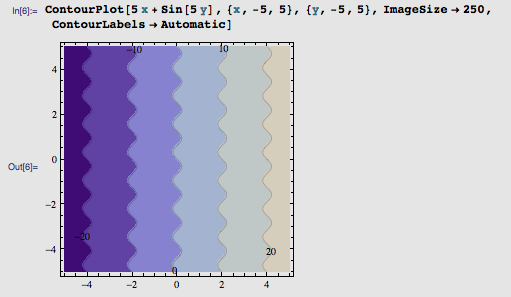
    这就有点裂缝的味道了。注意，图里看上去裂缝带有些宽，这无所谓——这只是生成图形中等高线画得比较稀而已。光从无差异曲线的分布形状来看，我们已经实现裂缝效果了。

    但是，怎样把这个裂缝应用到之前的心之函数里呢？注意到心之函数其实是一个不等式 17 x^2 – 16|x|y + 17 y^2 < 225 。如果我们能找一个两侧值小、靠近 y 轴部分陡然增大的波浪形函数 f(x, y) 就好了。把这样的 f(x, y) 加到心之函数上，就相当于给 y 轴附近的一个波浪形范围加上一个大得出奇的值，让不等式左边超过 225 ，出现裂缝状的空缺；同时，这以外的部分 f(x, y) 几乎为 0，该小于 225 的还是小于 225 ， 该大于 225 的还是大于 225 ，对心形不会造成任何实质性的影响。     什么操作能够让一个函数变得两边小到几乎为 0 ，靠近 y 轴的地方陡然增大呢？答案是“绝对值分之一”。   

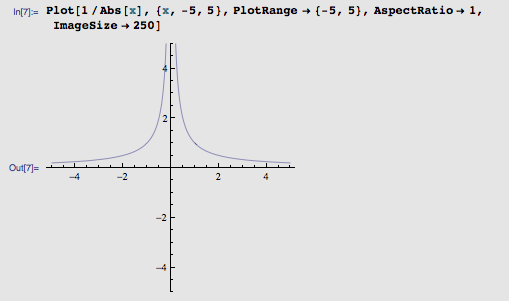
    把它应用到之前的 f(x, y) 上（函数也就变成 1/|5 x + sin(5 y)| 了）：

  

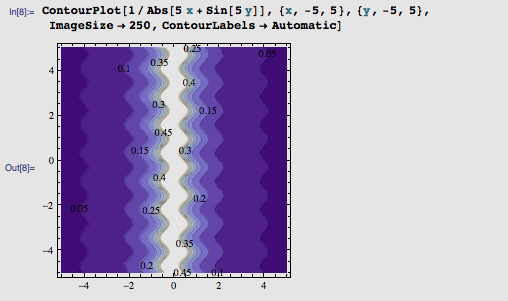
    哈哈，这个有效果，中间的函数值陡然增大，大到都亮得发白了。

    让我们把这个 f(x, y) 加到心之函数上，也就是说画出不等式 17 x^2 – 16|x|y + 17 y^2 + 1/|5 x + sin(5 y)| < 225 ：   

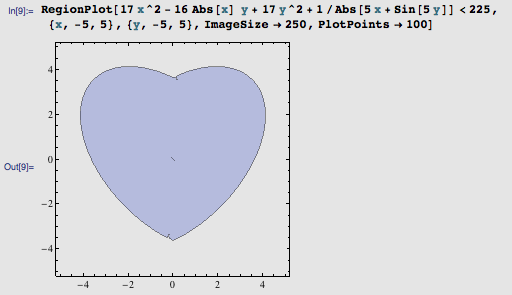
    咦？怎么没有效果呢？且慢，仔细看图的中间，已经有一些要裂开的痕迹了。我想到了一个可能的原因：裂缝带的函数值还不够大。心形图形是由所有满足 17 x^2 – 16|x|y + 17 y^2 小于 225 的点组成的，但是这些点的函数值并不是刚好 225 ，以至于加上了一个大数后仍然比 225 小。为了扩大裂缝的影响，让我们把 1/|5 x + sin(5 y)| 的分子改成 150 ：

  

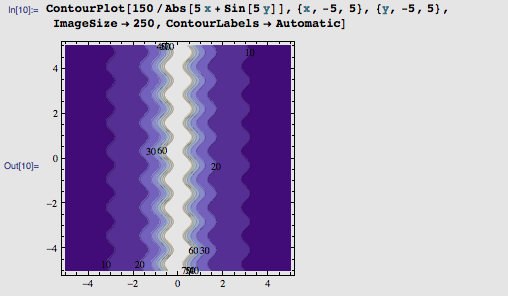
    让我们祈祷这次裂缝的函数值足以把心形破坏掉吧：

  

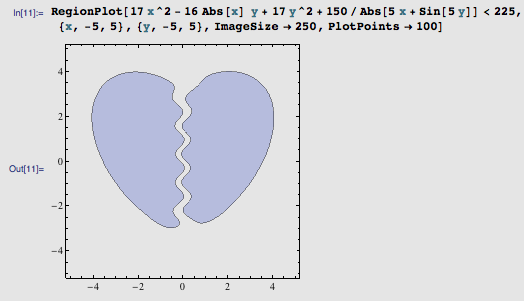
    哈哈，这次成功了，裂开的心形！我原创的“分手方程”就此出炉了： 17 x^2 – 16|x|y + 17 y^2 + 150/|5 x + sin(5 y)| < 225 。让我们把这个不等式本身标在图上，方便在网络上传播：   

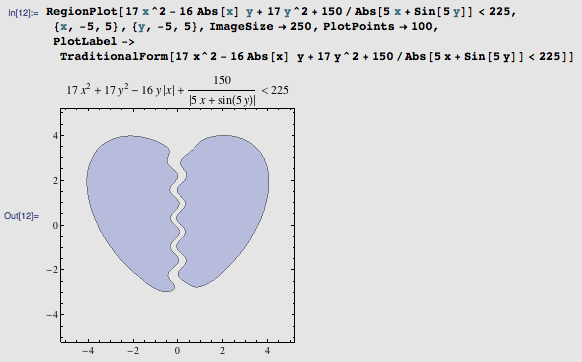
    不过，这个分手函数有一些美中不足的地方：它用到了分式运算，不能和已有的部分很好地合并在一起，很容易看出这是由心形函数和裂缝函数拼合而成的，看上去有些平凡。另外，对于某些特殊的取值（比如 x 和 y 都为 0 ），不等式左边有可能因分母为 0 而无意义，虽然在分母上加个很小的常数可以避免，但作为完美主义者我仍然感觉很不爽。

    这个方程有诸多不完美之处，如何构造一个看上去更酷的方程呢？写了这么多我也有些累了，脑子有点不够使了。既然“情侣去死去死团”年年都少不了 Geek 方阵， Geek 恋爱困境似乎百年不能动摇；如何寻找更完美的分手函数，不妨留着我们明年再来讨论。

75 条评论

发表评论




Enter Captcha Here :