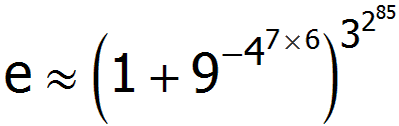
刚才看到这个很漂亮的无理数 e 的近似表达，它恰好用到了 1 到 9 这 9 个数字。
猜猜看它能精确到 e 的小数点后多少位？ 10 位？ 100 位？ 1000 位？ 10000 位？
远比想象中的牛 B —— 它能精确到小数点后 18, 457, 734, 525, 360, 901, 453, 873, 570 位！显然，这绝对不是一个巧合。它的秘密就在于， e 事实上等于 lim(n→∞) (1 + 1/n)^n ，而 9^(4^(7·6)) 恰好就等于 3^(2^85) 。这个指数相当大， Mathematica 直接就报 Overflow 了，难怪它能精确到 e 的小数点后那么多位。
据说，这个神一般的近似表达最早来源于这里。
这个，9^(4^(7·6))= 3^(2^85)，太巧妙了！ 9^(4^(7·6)) =(3^2)^(4^(7·6))=3^[(2^84)*2]=3^(2^85)!!!
不过照这个思路的话，是不是也会有其他的类似情况呢？想到一个简单的：n=(7^2)^(3+8)=49^(5+6),当然精度上就差很多了……
传说中的沙发？
狂晕，和沙发之差1s！
估计是网速惹的祸。
给个链接：http://bbs.emath.ac.cn/viewthread.php?tid=1776
神一般的近似表达！！！
1min, not 1s
我不是故意的……话说我还打了那么多字，再加上思考的时间……
这个式子。。。Orz
牛..
很囧的一个，数
我想验证这个等式：9^(4^(7·6))= 3^(2^85)
用windows自带的计算器，发现这两个数并不相等。用Excel，都超出数字的范围了。呵呵
9^(4^(7·6))=9^(4^42)=9^(2^84)=3^（2×(2^84))=3^（2^85)
理论上推导也是成立的，其实不用execl或mathematica等去算。
请问用什么方法可以验证两个数小数点后那么多位是一样的
可以用软件实现么？
LS，这个似乎是理论推导出来的？
请问lim(n→∞) (1 + 1/n)^n =e 这个是怎么证明的？我很菜，这是我同学的考试题目……
LS，这个应该回去翻高数
这个比较牛……
回15楼
这个似乎是e的定义之一，参考资料：
http://zh.wikipedia.org/zh-cn/E_(%E6%95%B0%E5%AD%A6%E5%B8%B8%E6%95%B0)
喔 答案是什么？
表示刚刚学了高等数学
e=(1+1/x)^(x)
文中式子符合这个定义。
以后要是看到不会的题，有答案和解释就更加完美了
最接近π:
213/67.8-5^(-9.4)=3.1415926513975351299391907392069