显然，过 Pizza 的圆心作四条直线，把一个周角平分成八等份，则整个 Pizza 饼也被分成了八等份。我们也很容易联想到，如果过圆心外的一点做出四条直线，并且同样满足每两条相邻直线夹 45 度角，那么这八块 Pizza 饼显然是不一样大的。考验你直觉的时候到了：你认为蓝色面积之和与红色面积之和相比，哪个大一些呢？

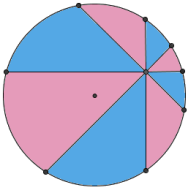
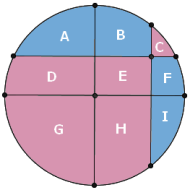
    事实上，蓝色面积和红色面积一样大。但请注意，这绝对不是显然的。下面这个事实估计会让不少人吃一惊：如果题目改为两条互相垂直的直线，那么红色（圆心所在的颜色）的面积是大于蓝色面积的。证明这一点很容易，我们只需要说明红色面积之和减去蓝色面积之和大于 0 就可以了。而容易看出 G – A = D ， H – B = E ， I – C = F ，并且还有 D – F = E ，于是

    (D + G + E + H + C) – (A + B + F + I)
  = [(G – A) + D] + [(H – B) + E] – [(I – C) + F]
  = 2 * D + 2 * E – 2 * F
  = 2 * (D + E – F)
  = 4 * E > 0

 
    今天，我看到科学松鼠会上谈到了 Pizza 定理，正巧我最近也读到了很多与 Pizza 定理有关的东西，在这里与大家分享一下。正如小易所说，前不久， Rick Mabry 和 Paul Deiermann 证明了下面这个猜想：用 N 条等分周角的直线切一个圆，当 N 为大于等于 4 的偶数时，两种颜色的面积一样多；当 N = 1 、 N = 2 以及 N 除以 4 余 3 时，圆心所在的颜色拥有更多的面积；其它情况下（ N 大于 4 且被 4 除余 1 ），圆心所在的颜色拥有更少的面积。这个证明很长，我自己也没有读完过。但值得一提的是，对于 N = 4 的情况，之前人们曾发现了不少值得膜拜的证明。
    1994 年， L. Carter 和 S. Wagon 利用几何软件 CABRI 发现了一个割补法证明，得出 N = 4 时两种颜色的面积确实是一样大的。我做了一个 GIF 动画，直观地显示出了整个“证明”过程，真可谓是神来之笔。有几块区域的全等需要严格的证明，不过也非常容易，这里就不再赘述了。

 
 
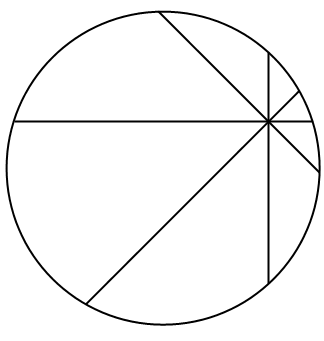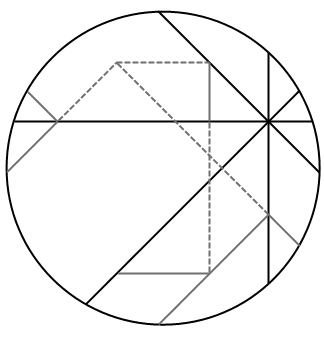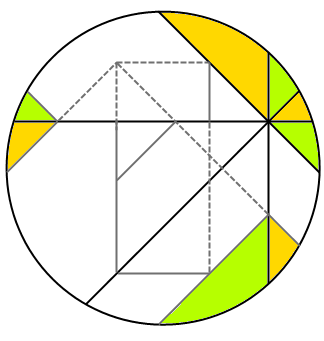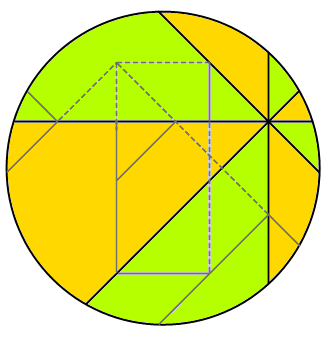
    利用积分思想， Jörg Härterich 给出了一个更美妙的证明。证明的关键在于下面这个引理：在半径为 R 的圆内有任意一点 P ，过 P 做两条互相垂直的直线，与圆产生四个交点，记 P 到这四个交点的距离分别为 a 、 b 、 c 、 d ，则 a^2 + b^2 + c^2 + d^2 = 4*R^2 。

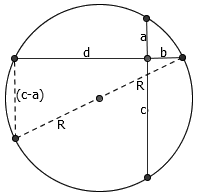
    证明很容易，由勾股定理，显然有 (c-a)^2 + (b+d)^2 = (2R)^2 ，同理 (d-b)^2 + (a+c)^2 = (2R)^2 ，两式展开后一加，结论就出来了。
    现在，把 P 点当作极坐标的原点，假设 Pizza 的半径为 1 ，令 r(θ) 表示 P 在 θ 方向上到 Pizza 圆周的距离。把面积看作一个个小扇形面积的积分，由于扇形面积等于半径的平方乘以弧度的一半，因此红色面积就等于

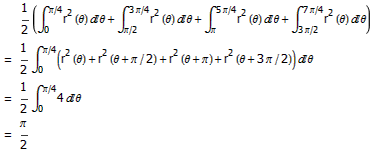
    正好是整个圆面积的一半。

    虽然 N = 4 的情况有了不少漂亮的证明，但当 N 更大的时候，问题将会变得出奇地复杂，分析时需要用上一些更玄妙的手段，几十年的时间里愣是没人搞出来。附上 Rick Mabry 和 Paul Deiermann 的论文原文，大家若有兴趣的话可以研究一下。