IBM Ponder This上个月的题目比较有趣:我在心里面想一个2到166之间的整数(包括2和166),你的任务是用尽可能少的是非问句(我只能回答是或者否)猜出这个数除1以外的最小约数是多少。
(1) 寻找一种策略使得在最坏情况下猜到答案的询问次数最少。
(2) 寻找一种策略使得在平均情况下猜到答案的期望询问次数最少。

第一个问题很容易回答。虽然2到166之间的整数一共有165个,但它们的最小约数(以后我们说的“最小约数”都是指的不包括1的最小约数)只有38种。因此,事实上你只需要用二分法在38个可能的答案当中找出一个就可以了。由于2^5=32,2^6=64,因此最坏情况下需要6次询问才能保证猜到。
真正困难的是后面一个问题:要想让平均猜测次数尽可能少,我们该从哪里入手呢?
为了方便思考,不妨让我们把这个问题简化一下。假设题目条件中我心里想的数字范围是2到10之间的自然数,由于这些数的最小约数分别是2、3、2、5、2、7、2、3、2,只有四种情况,因此只需要两个问题即可问出答案——比方说,第一次问“最小约数是2或3吗”,回答“是”则再问“最小约数是2吗”,回答“否”则问“最小约数是5吗”,即可保证知道答案。若采用这种策略的话,不管我心里想的是什么数,你总是需要恰好两次猜测才能猜出答案。但事实上,由于最小约数是2的可能性远远大于其它的数,因此减少最小约数是2时的猜测次数,增加最小约数是5和7时的猜测次数,虽然最坏情况下需要的猜测次数变多了,但我们或许能得到更优的平均猜测次数。我们可以这样做:先问“最小约数是2吗”。如果回答是,则直接猜到,因此当我心里想的数是2、4、6、8、10中的一个时,猜测次数仅为一次。如果回答否,则问题变为了下述子问题:当我心里所想的数为3、5、7、9时,平均需要多少次猜测才能猜出它的最小约数?对于这个子问题,我们同样发现,由于最小约数为3的概率较大,因此直接问“最小约数是3吗”更好。采取这种策略,我们可以看到:当我心里想的数是2、4、6、8、10中的一个时,只需要一次猜测;当我心里想的数是3或者9时,需要两次猜测;当我心里想的数是5或者7时,一共需要三次猜测。因此,采用这种策略平均需要(5*1 + 2*2 + 1*3 + 1*3)/9 = 15/9 ≈ 1.67次猜测。
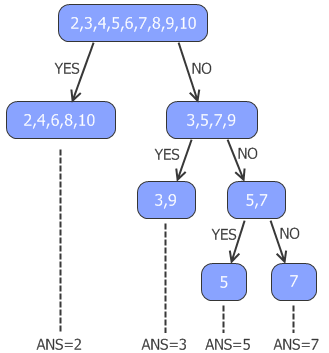
觉得上面的图是不是很熟悉?当你把上图从下面倒着往回推时,你会发现这是一个经典的贪心算法问题。我们把拥有相同最小约数的数放进一个集合,则得到的四个集合分别为{2,4,6,8,10}、{3,9}、{5}、{7}。把两个集合合并成一个大集合,直观意义就是这两个集合是由一个大集合通过一次询问划分出来的,此时总的询问次数就增加了两个集合总的元素个数那么多。借用类似于Huffman编码的算法,我们立即想到,不断合并当前元素个数最少的集合,得到的总猜测次数就应该是最优的。利用Mathematica求解原问题,我们可以得出,对于2到166的情况,平均494/165=2.9939…≈3次询问就能找到那个最小约数。
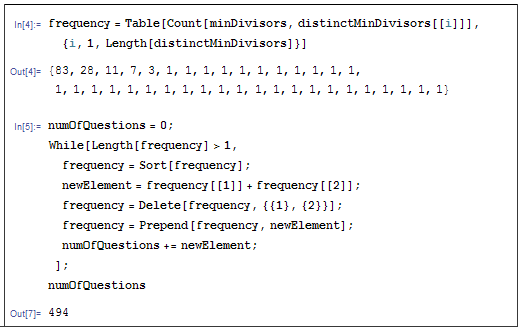
当你联想到了Huffman编码时,你会惊奇地发现,原问题完全等价于Huffman编码问题。注意到“猜到最小约数”的意思就是说,每一个可能的答案都对应着一个YES/NO序列(也就是一个01串),且任一序列都不能成为另一个序列的前缀。而这些最小约数的频次是不同的,因此我们需要给所有可能的最小约数进行二进制编码,使得它们的加权长度最短。这就是一个典型的Huffman编码问题了。