上次说到维度时，有人提到了如何理解四维空间的问题。这是一个非常有趣的话题，可是我一直没有用心写一下。前段时间网上出了一部片子叫做Dimensions: a walk through mathematics，据称里面详细介绍了四维空间。我本以为推荐一下这个片子就能少写一篇又臭又长的日志了的，没想到下下来看了之后发现该片奇差，不了解四维空间的人看了半天估计还是不了解四维空间。最近放假比较闲，打算慢慢来扯一下。如果你以前从来没细想过四维空间的话，相信今天你会有一种超凡脱俗的感觉。
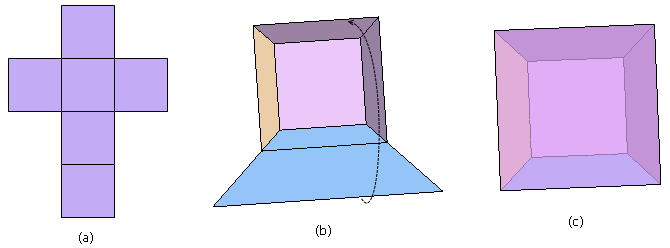
现在，假设我是一个二维世界的人，我不能理解什么是“高度”，什么是“体”，什么是“空间”。你想向我描述三维世界中的立方体。你该怎么说呢？你或许会从立方体的展开图开始谈起：图(a)就是一个立方体的展开图，如果我们剪一个这种形状的纸板，我们可以把它折成一个正方体。我开始好奇了。
– 你说说该怎么做呢？
– 先把上面几个正方形折起来，把对应的边粘在一起……
– 等会儿呢等会儿呢，这几个正方形是稳定的形状呀，它们的边怎么可能挨到一起呢？
– 傻了吧！在二维世界中它们不是活动的，但是它们可以向第三维度弯折啊！给你画一个图(b)吧，这就是把上面那几个正方形粘合起来的样子，这就成了一个没有封顶、还差一面的正方体……
– 你耍赖！你这样弯折了之后正方形都不是正方形了，都变成梯形了！
– 不对，它们仍然是正方形。图(b)的六块区域其实都是正方形，只是由于透视作用，它们看上去好像变“斜”了。
– 嗯，好吧，你继续。
– 现在我们得到的是一个有盖的盒子。上面五个正方形（其中有四个由于处于第三维度而变了形）的“内部”已经形成了“空间”了，可以往里面放东西了。要想做成一个封闭的正方体，只需要把剩下的那个正方形合上去就行了，最终结果就像图(c)那样。
– 咦？图(c)里面，刚才最后要合上去的那个正方形到哪儿去了？
– 它就是最大的那个正方形。
– 胡说！那个大正方形是五个小正方形拼成的！这个大正方形刚才在图(b)里也有！
– 不是的。图(b)里的大正方形的确是五个小正方形拼成的轮廓，但图(c)里的那个大正方形是真实存在的，它就是最后合上去的那一块。这个大正方形也并不是和那五个小正方形重叠在一起，它们在第三维中的层次是不同的。图(c)就是你梦想的那个正方体了，它由六个正方形组成。你在图(c)中看到的一个小正方形，一个大正方形，四个梯形事实上都是正方形，而且它们都一样大。这六个正方形围成了中间的那个“空间”。
– 我还是不明白。那个大正方形也是在第三维度的，为什么它没变形呢？
– 这是因为，这个正方形所在的方向不是第三个维度，因此看上去和原来一样。
– 那同一个方向上为什么又有一大一小两个正方形呢？
– 唉，真麻烦。这是因为，它们的朝向虽然一样，但在第三维度上的位置不一样。小的那个正方形在第三个维度离我们远一些，看起来就要小一些。
– 哦！我有点明白了。是不是说，旁边一圈那四个“正方形”是跨越了第三维的，因此在第三维空间中一部分离我们近，一部分离我们远，于是看上去就是由大到小渐变过去的，就像是变形了。
– 对！你理解得很好！说真的，平时生活在三维空间中，我都还没仔细想过这一点呢。
– 我好像真的明白了，说错了不要笑我哦。那个“空间”啊，说穿了就是大正方形擦着四个变形正方形在第三维度上向远处的小正方形移动所产生的“轨迹”。
– 正是正是！
– 哎呀我彻底明白了。怪不得我们说n维立方体有2^n个点呢，其实道理很简单。其实只需要把n-1维立方体复制一份，然后对应的顶点相连就可以了。这就是n-1维立方体在第n维发生位移的结果，新增的那2^(n-1)条边就是点的轨迹。
– 哎呀，你太他妈牛B了，读中文系真他妈可惜了。我还给你看一个好玩的东西，让你看看三维立方体是如何旋转的。睁大眼睛仔细看好每个正方形都变到哪儿去了。
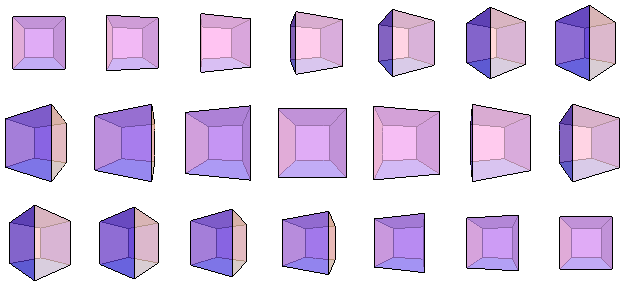
– 我又糊涂了。为什么从第三幅图变成第四幅图时，远处的小正方形能够穿越左边界，让其中一小半跑到边界左边来？
– 这个确实不好理解。小正方形并没有“穿过”那条竖直的边，那条边在第三维上离我们更近，而它在我们这个方向上的投影又与小正方形重合了。其实你可以看到，它们之间的拓扑关系仍然是不变的。
– 哦，于是乎远处的小正方形就转到侧面去了，然后又转到离我们近的位置来了，替代了原先大正方形的位置……
– 回去没事多想想吧。期待你睡觉时能够做出一个三维的梦。
– 好的。谢了。
好了，现在呢，告诉大家一个秘密，其实我是来自四维空间的人，很多人问我四维立方体是啥样子的，烦死我了，于是写下了今天的这篇日志。
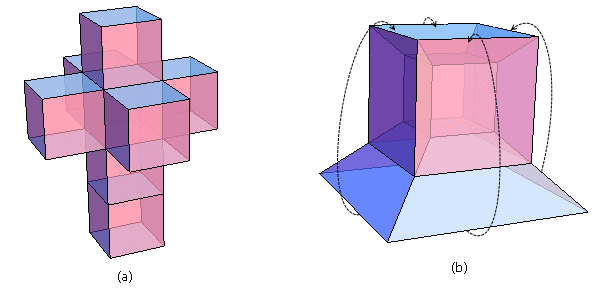
现在我告诉你，四维立方体是由8个大小相同的三维立方体组成，其展开图如图(a)。图(b)是粘合出来的四维盒子，还差一个盖子没有盖。这些看起来像棱台的东西其实都是根正苗红的正方体，只是由于它们在四维空间中位置不同，发生了透视。
把盖子盖上后，我们就看到了传说中的四维立方体，这个图形相信很多网友已经很熟悉了。图上有一大一小两个标准模样的立方体，这是第四维度上位置不同但都正对我们的两个“三维面”。其它棱台其实都是正方体，只是看上去因透视而变形。四维立方体可以看作是三维立方体的移动轨迹，因此画一个四维立方体很简单：画两个三维立方体，然后连接对应顶点即可。观察四维立方体的旋转，你会看到里面的小立方体穿过一个面跑到了外面，而后又变成了最外面的大立方体。这一切都和二维向三维的推广是类似的。仔细观察思考，你还会发现更多可以类比的地方。
果然抢到了沙发
楼上真有时间,那么早起来抢沙发
严格地来说,最后那个旋转图上,用于照射四维体的光,好像是按照三维的方向发散的……
我又是接近了LZ
啊？这是今天的？Orz
你太tm牛13了，佩服佩服……
牛，好
我转载了
抢占一个高点的先
还有四维的“旋转” 应该是以“面”为“旋转中心”旋转的？
现在想明白了，做四维CUBE是粘合平面的。。。。
对了问下，为什么是8个立方体组成的呢
ps：现在正在对四维的球YY
巧了我也有这个疑问，我觉得是七个啊
哇，长见识了。
有种数学版的Sophie’s World的感觉，真的很棒！
不过我还是没想象出来真在四维里面是什么样。。
能否帮忙做一个四维的扫雷？
赞！
去中文系是为了让你成为恩格斯级的大牛啊！
m67偶爱你~
话说偶看了Dimensions的确是看完还是不知所云。
不过……我还是有个疑问的说
如果你是一个二次元的人，用何种方法才能看到平面图形呢？
向二次元描述三次元是不可能的吧
N次元的人只能看到N-1次元的事物，而那个向二次元解释三次元的问题，
前提是在于让他看到一个平面图形
真的好神奇
理解
Dimensions: a walk through mathematics
里面那个转的东西是什么了
@16L：可以让他看二维图形在一维线段上的投影啊……
@地核：这个问题很好，建议看看《从一到无穷大》
“背景”变化的游戏都可以看成是高维投影啊，就像你之前介绍的Closure，其实就等价于 人物在三维空间里移动，“地面”是一块浮空的板，不过是斜的（不是高度变化那种）。这第三维取决于灯在画面的位置。人带着灯时只能沿着“斜”的方向移动，放下灯时只能在一个垂直的平面内移动，合起来也算是自由移动了。
本人来自第五维空间，让我给你解释下第五维空间：
@#$^@%^%$&^#%*^%#^$#@#$&^#%
%^%#&%^&%&@#%^&*^$*&^$*(#&%
@^%$%&$^*&&^*@$^$#$#@%#$%%^
……
强文留名
牛×啊
我想起了伽利略的《对话》
Deminsions 里的说明也很精彩, 顶这篇blog
在大爆炸之初，没有空间没有时间，没有维度。
那大爆炸之后，就算按照超弦理论的11维，又是为什么正好这么个维度数呢？似乎并没有任何规则限定了宇宙诞生之初应该是多少维的。
to：16楼
你说的正解，这么长篇大论其实都只能在脑子里面意会，如果存在二维世界的话，他们看见的东西永远都是一条线，不对，应该是一条理论上的“线”。根据博主的推断方法，其实三维世界的我们所看见的也只是三维物体在我们的眼睛上投影然后在大脑里形成二维影像。
如果一个二维生物能看见博主那幅图，那么观察者与被观察的图形之间的距离就应经形成了第三维度。
所以低维度想要窥视高维度，永远也只是YY的事情。因为无法理解。
至于博主的四维，那就要看这个第四维是怎么定义了。如果定义为时间线的话（以上只是YY哈），用色泽浓浅表示时间的单位度。那么三维的我们就是看见N个物体影像的无限重叠。当然，前提是这玩意没有移动。要不是什么样，只有四维的生物，不对，如果时间是维度，就不存在我们意义上的生物，应该说是存在，知道了。
根据强人择理论，我们的宇宙之所以是这样的，是因为有我们
我还是去个墙角好好珍惜我们的世界吧。。。。。。
27L 很无语的说 M67大牛是以很严谨的科学态度讲这个东西的 居然还在这里锻炼自己的YY能力
对这个无限感兴趣ing…
to 27L:看的是一条线也无所谓,不是有透视吗.话说我们看见的”四维立方体”不就是二维的透视图吗
一直觉得多维世界很神奇
好多图 。
强悍，再次体会到lz的强悍
我无法理解你们这些生活於三维世界里的人的想法
除了八个方位与上下两个方向外,你们真的从没想过其实还有别的移动方式吗?
在我看来,你们的行动范围实在是极为狭窄,受尽限制…你们当真从来没有意识到这点吗?
既然点、面、线是形成1、2、3维度，那么水和空气呢？
西游记真假美猴王中的地府灵兽谛听能通晓四方上下古往今来之事，或许就是能在四维时空中自由穿梭的怪物吧。
……其实，有一本叫《从一到无穷大》的书解释得很清楚啦啦啦
非常凑巧，我的博客最新写了一篇日志也是关于四维世界的。不过您的讲得十分生动而且幽默！
to 30L
……怎么说呢？也许您的YY和思考泾渭分明，一丝不苟。做学问不就是相互辨证吗？我说出我的想法，你也可以指出我的不正确的地方，相互学习，共同进步吗。
to 32L
我的意思是理论上的一条线，也就是说，在我们这个世界是不存在这样的线的。因为你画的无论多细，还是会存在一个高度的。当然你可以试着突破咱们这个维度的最小距离单位，那么世界的未来就靠你了。
既然没有实际意义上的高度，那么这个2维的物体所看见（其实应该不存在看见）的东西无非就是有和无以及之间的变化，或者说意义上一个维度的深浅变化。想看到平面或者所谓的透视，那么他就到了咱们3维的世界了。因为没有高和宽的话，如何表现近大远小的透视效果。……除非他抬头，要不就是一条深浅不一的线。
在下读书不多，以上就是结合看过那些少得可怜的书自己琢磨的想法，也就是YY.欢迎讨论，大家共同进步。
16楼说的不错。二维空间的人只能看到一维的。我们三维空间的只能看到二维空间。就算是那个所谓四维空间的图片实际上也是二维的……只是我们想象成三维，就是三维的投影
http://www.youtube.com/watch?v=HvgwR9ERCBo
一个有关维度的动画
等三维显示器普及了麻烦再表示下四维空间吧
学中文可惜了。。。ng。。。
我认为 研究多维空间 不是要用这种想象的办法,而想要用转换的方法..
想象的话 会加深思维深度, 简单的图形可以, 复杂的 根本想象不了.
在数组用有1,2,3,4,5…N维数组, 但是计算机里表示最终还是可以表示成一维的
几何也类似再多的维度 都可以表示成一维 但由于1维构不成几何 转换成2维最合适 二维就是面. 三围 可以看到3个面 立方体对称 所以有6个面
4维的立方体呢 对称 可以看到4个三维立方体 所以 有8个三维立方体. 一共有48个面
5维 可以看到5个 (8个三维立方体) 对称的话有10个(8个三维立方体) 也就是有80个三维立方体 一共有480面
6维 可以看到6个80个三维立方体 对称考虑 有12个 80个三维立方体 就是960个三维立方体 共有5760面
……………………
或许我考虑的不对 比如在对称方面, 但思考多维几何 抛下砖
比如 什么是三维函数 可以理解成 一张张二维函数叠加起来
四维 就是 一个个 三维函数叠加起来….
27楼说的是没错, 哲学上讲,笛卡尔也阐述过,现在的确是四维空间 物体三维+时间一维 事实上由于时间的不可逆性 它只能算半维 所以 现在是3.5维 不是么?
看来我太蠢了…
好神奇啊
他妈的你竟然去中文系了。。。哎。。我这个工科学生很惭愧啊
和我想的一模一样!不过我只是个高中一年级学生.
我费了三天三夜苦思冥想,终于想出来了!还以为能拿诺贝尔奖呢,
原来早就有人研究了!无语….
从8个三维立方体变成四维立方体，最后那个是怎么完成的我想象不出来
我有一个问题：从二维到三维的变化是基于人的感官和经验，但是人类可能对四维全无经验，那么在已有从二维到三维的基础上，凭什么就说三维到四维的过程是这样的；二维到三维的已知正确凭什么就能得到这里说的三维到四维变化的正确，怎么证明，怎么推断？
回复 52楼
四维立方体很科学,完全不是瞎想.
回复 46楼
你那个公式错了!过些日子我告诉你吧
36楼的说的不错，一维X，二维是X,Y，三维是X,Y,Z,四维是X,Y,Z,W,前面几个我不用解释了，你们都已经知道了，只有W，你们还不知道，很多人都说是爱因斯坦说的时间轴，不是，而是在长，宽，高之后加上一个厚度，其实我们就存在四维空间中，就如同二维存在三维中，在二维中你不可能造出三维的东西，要不然，你就不在二维中，因为在二维中没有这个能力造出三维的东西，我们现在也一样，拿三维的技术来造四维的东西。不过现在有电脑，在电脑里是可以达到的，另外，说一声，时间对在四维空间里存在的生命来说是没有意义的，还有人要想穿越四维空间就要在三维空间里拉开一个洞，才能到达我们现在无法到达的地方。一个进入过四维空间的人。
http://schuyler.cn/archives/747
人眼看到的，一直都是四维时空
我是11维世界来的……
无限感兴趣,看完后一直狂晕中….
喜欢探秘,但是好深奥太深奥….
无奈我只是个做销售的
http://shop35962995.taobao.com/
下辈子我要去往做研究做学问的方向发展去
刚发错了所以重新发了一下
看来我还需要增强一下严谨的态度
还有请楼主帮忙删除我之前的两个回帖哦
既然楼主是中文系的，为什么文不对题呢，篇幅90%是在解释3唯空间，地球人都明白的不是么`那么多图案无非就是在讲一个立方体，对话也完全是在解释2维到3维的转换，对于你最后4唯空间你却只是稍微提下`在这里并不是在质疑楼主，也不能完全否认你是4唯的人，但是请以一个四维思想的人来解释4和3之间的鸿沟，而不是象文章中解释3和2之间的联系，所以如果楼主是来自4维的人，期待你能以这篇的对话模版去解释3和4间的转换~
应该不是二维推三维这种方法吧？
一维推二维怎么解释。。。。。
OTZ！
仍然没有脑像……要是我是魏成就好了……
@ 59楼：
写这么多是为了让你用类比的方法按照从二维推广到三维的方法思考从三维如何推广到四维。。
我的妈呀，果然超凡脱俗～
前面二维到三维的铺垫，很重要的。
最近迷上四维空间了～
不过到底是真实存在还仅仅是一种思维游戏？
我明白了，我明白了，我完全明白了。
的确让人茅塞顿开，原来我们只是三维空间的小生物 生活在思维空间的人一定会笑我们一直在走弯路，呵呵
LZ有意无意没有点透一个事实：那个所谓4维立方体，只是真正的4维立方体在3维空间中的正投影；4维立方体在第4维方向上的转动投影到我们3维空间，则形成了那个小立方体穿过大立方体的动画
上面所有说已经明白的人，其实都没有明白这一点：LZ画出来的所谓4维立方体，只是一个大块套小块的3维物体，是4维物体的3维空间投影而已。别着急，我问您，4维立方体真是你看到的这个样子么？你确定？一定？？以及肯定？？？
残酷的事实是：一个3维空间的生物，不可能想象出一个静态的4维空间物体的真正形状，只能间接模拟，这个想象的形状实际上还是三维或者更低维的。
有人说第4维不就是时间么？！这个说法显然不准确。时间这一维跟空间的3个维，其别还是很大的，首先在衡量尺度上就相差很远，其次时间是有方向性的。在广义相对论的范畴内，由于存在光速这个常数，因此时间和空间可以在数学上进行变换。（你可以简单理解为，时间长度可以变成空间长度，你看看“光年”这个空间距离单位！就是光跑的一年的时间啊）因此时间看作第4维在数学上是可行的。
既然我们生活的空间是3维的，那么很显然第4维就不在这个空间里，它存在于我们看不见的地方。我们了解它的性质，感受到它的存在，却永远不能切切实实的触碰到他。姑且安慰下自己，也许4维空间只是数学家的想象呢
请M牛大哥解释我们二维生物的目光是如何离开我们所在的两个维度，感受到第三个维度的？
或者这么解释，当一个动态的正方体投影在一个二维世界中时，二维生物如何只通过对”前”和“后”的充分理解，来理解一个超然二维之外的正方体存在？
或者说，M大，按照“二维世界的直线最短原理”，当我的视线穿过一个二面角时，我是无视该二面角的存在的。
或者说，M大，这样当一个动态的正方体无视了空间结构（而非所谓的压缩），通过投影的方法，将它的一个侧面展示到我的二维世界中时，我如何通过对这个动态的二维图形的充分理解，重建这些边之间的视觉关系和数学关系？
M牛大哥，我这么类比吧，当人们在一个三维坐标上确认一个点时需要（x,y,z），当在上确认一个点时，需要（x,y）。但是当在莫比乌斯带上x轴的定向出了问题的时候，即使直线最短，我也依旧无法通过坐标定位这样一个二维世界中的点。
或者说，当我一个二维生物躺在一条超级大的莫比乌斯带上，在这个“平直”的世界中，沿着x轴看到远方我的后脑勺的时候，我如何认定这个后脑勺就是我的呢？
类似的，在这个世界中看到我的后脑勺，我就知道世界有多大了吗？
回到四维在三维和二维上的投影，我这个二维的孩子想明白这个该死的正方体平面透视图凭什么可以这么动感，这么美。
其实，二维生物也许也可以对二维图形有个整体认知吧。
虽然是只能看到线，但是假如生物与图形不在同一个面上，就可以做到像扫描一样观察到二维图形内部的线，好像 三体三 里进入四维的人可以看到三维的无限细节一样。
难道对于维度来说一直有两种说法，一种是第四维是时间，还有一种是空间意义上的第四维？？？
四维还好懂，后面的我就萌了，LZ能说的通俗点就好了哦，关注你那么久了，这个页面做收藏夹，可是看了N多遍都没有完全理解，艾薇让我大脑锈了？
这个，除非用代数方法在一边详细对应着解释，否则我真的看不懂。
对这个4维面上的原子来说 是不是他就是7维了 如果我们是7维 宇宙是4维 对宇宙来说 是不是就是11维呢 胡思乱想 呵呵
建议楼主将二接三的对话写一份三接四的，这样不用堵住自行类比，也许更有助理解。
对不起，打字错误。更正：『不用读者自行类比』。
唉……这些问题我都想过，但仍然没法凭借空间想象力去想象高维空间。正交坐标系的描述倒是很容易，不过那就失去“图形”（或者应该说“图体”？）本身的意义了……
还是解析几何来得更为简洁,更为严格些
还是一头雾水，确实很难想象
哇，长见识了。
看完以上全部留言后 55楼所写的是最让我惊讶的 其他的那些概念都可以推理或者以此类比出来。 看完留言后个人认为，第一：N维的人的视觉是N-1维。第二：N维的人能理解和创造N维的事物（通过观察N-1维 来判断）。第三：N维的人只能了解N+1维的性质。 记得有一本书叫做spaceland,讲述的是 对于平面国的人来说空间国的人是神 因为他们能在不破坏保险箱的情况下从里面拿走东西 也会突然出现或消失，也能看到平面国的人身体里面的所有细节。 我觉得之所以我们能做到这些是因为我们看二维事物的时候 它们对我们来说是平面的 ，相反的，之所以二维的事物看不到自己的内脏是因为 它们的世界对它门来说不是平面的。换句话说 我们在＂系统＂之外 所以才可以变成＂神＂。这里的问题就是 如何跳出来此 ＂系统＂，答案是 没办法，就如同我们没办法让书里的漫画人物 跳出来 变成立体的。回到55楼所说的 划破空间 进入四维 理论上 存在 但是永远无法触及，也无法感受到 站在四维看三维的感受（如同二维无法感受到三维是如何看到二维的）
有很多人都认为，某图中那个东西是超立方体的三维投影。我觉得不妥，因为我们看到的景象是二维的，只不过我们能用双眼将实物看得立体。因此我觉得图片上那个也是二维的投影。大神觉得呢？
完全不能理解！！如果我是二维空间的人的话根本就不可能理解透视这个概念！就算我是三维空间的人，透视也是作为常识，一个不可分解的基本概念在运用，也不知道透视为什么会产生，只能接受，作为常识理解。而且，第四维的方向在哪一边？定义状态下，第四维在哪边我都不知道！你还和我说第四维产生的透视！我就更不理解
如果4维立方体是8个3维立方体组成的，那么5维立方体就是10个4维立方体组成的啦~ haha~
写得太好了，感谢
应该是三到七
4维空间只是假想，不存在的东西
二维生物是完全意识不到图形的。因为图形也是三维世界的东西。他只能看到一条线折叠之后变短了而已。
aming路过、正在无限探知中…
沙发上我的( ͒•·̫|有无王者