你认为,一个函数图象里是否有可能包含这个函数本身的“图象”?难以置信的是,还真有人构造了这样一个东西。2001年,Jeff Tupper发表的一篇论文里提到了这样一个有趣的不等式:
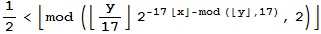
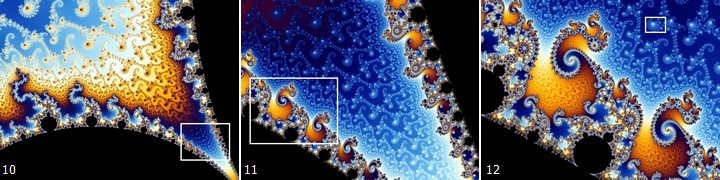
在0 <= x <= 105,n <= y <= n + 16的范围内,这个不等式对应的图象是这个样子:

其中,n = 96093937991895888497167296212785275471500433966012930665150551927170280239526642
46896428421743507181212671537827706233559932372808741443078913259639413377234878
57735749823926629715517173716995165232890538221612403238855866184013235585136048
82869333790249145422928866708109618449609170518345406782773155170540538162738096
76025656250169814820834187831638491155902256100036523513703438744618483787372381
98224849863465033159410054974700593138339226497249461751545728366702369745461014
655997933798537483143786841806593422227898388722980000748404719
你会觉得这个很神奇吗?你也许会想,天哪,这个是怎么构造出来的啊!但仔细思考之后,你会发现这个一点都不神奇。事实上明白了道理之后你可以构造出无数个这样的式子来。现在给你一些时间让你思考一下,你能否看出其中的奥秘?
就像魔术揭秘一样,说穿了真相后上面的这些东西就一点意思都没有了。在这个式子里,涉及到x和y的变量时都加上了取整符号,因此整个图象都是一格一格的。这样,不等式右边的式子就简化为y div 17 * 2^(-17x – y mod 17) mod 2,其中x和y都为整数。接着观察,一个数乘以2的负k次方相当于对应的二进制数右移k位,那么x * 2^(-k) mod 2实质上就是二进制数x右起第k位上的数字。对于某个自然数t,当17t <= y < 17(t+1)时,指数-17x – y mod 17恰好对应所有的负整数,于是位于y=17t和y=17t+16之间的图象的每个像素和t的二进制中的每一位数字一一对应。随着t值的增加,图形的像素会一点一点地变化。当纵坐标足够大时,必然会出现一段高度为17的图象,图象的样子和不等式本身的样子相同。当然,你也可以在里面“找到”任何你想要的图象,只需要把图象还原为二进制数并转换为十进制即可。你甚至可以告诉你的MM,说你发现了一个函数,函数在某个位置的图象正好是某某某我爱你的字样。
Matrix67原创
转贴请注明出处
最近发现了一些很不厚道的人,希望大家注意哦!