23. 一些硬币互不重叠地放在桌上。四色定理告诉我们，若要对硬币进行染色，使得挨在一起的硬币颜色不同的话，最多只需要四种颜色就可以了。存在至少需要四种颜色的构造吗？
答案：存在。如图，若只允许三种颜色的话， A 的颜色必须与所有阴影硬币颜色相同， B 的颜色也必须与所有阴影硬币颜色相同， A 、 B 将会同色。
书籍介绍
Which Way Did the Bicycle Go 趣题选（中）
14. 有意思的是，在数学历史上，一些很简单的结论竟然几百年来都未曾发现。直到 1977 年， Paul Erdős 和 George Szekeres 才发现，除了两头的 1 以外，杨辉三角同一行内的任意两个数都有公因数。证明这个结论。
答案：只需要注意到， a 乘以一个比 b 小的数之后还能成为 b 的倍数，这说明 a 和 b 一定有公因数。不妨设 0 < i < j < n ，则 C(j, i) < C(n, i) 。我们的命题可以由下述关系直接推出。 C(n, j) · C(j, i) = n! / (j! (n - j)!) · j! / (i! (j - i)!) = n! / (i! (n - j)! (j - i)!) = n! / (i! (n - i)!) · (n - i)! / ((j - i)! (n - j)!) = C(n, i) · C(n-i, j-i)
Which Way Did the Bicycle Go 趣题选（上）
我找到了这道经典智力题的出处。它似乎来源于一本叫做 Which Way Did the Bicycle Go 的书。这本书又是一本超赞的趣题集，里面有很多我没有见过的趣题妙解。我找到了这本书的电子版，并且传到了自己网站上，与大家分享一下。大家可以点击这里下载。阅读器可以在这里找到。
我整理出了个人认为比较精彩的题目。如果你没有时间翻遍整本书的话，看看我精选出的这些题目也是一个不错的选择。
1. 给定 △ABC ，对于平面上的任意一点 X ，它属于点集 S 当且仅当线段 BC 上存在一点 D 使得 △ADX 是等边三角形。点集 S 是什么样子的？
答案：两条线段，它由线段 BC 绕 A 点顺时针或逆时针旋转 60 度而得。这是因为，给定 A 点和 X 点，则 D 点的位置可以由 X 点绕 A 旋转 60 度得到的。既然 D 点在 BC 上，那么显然 X 点就应该在 BC 绕 A 旋转 60 度得到的线段上。
漫话科学哲学：什么是科学解释？
小时候我就很喜欢思考一些科学之外的东西。数学家发现新定理，物理学家提出新理论，发明家创造新事物，自以为无所不能的科学似乎已经统领了整个人类历史的发展。但是，谁又来思考科学本身呢？于是我常常幻想，如果当初科学没有战胜宗教，世界又将怎样？人类依旧停留在穷困的黑暗社会？还是与大自然和睦相处过着无忧无虑的幸福生活？甚至是凭借直觉和信仰建立了一套能够自圆其说的物理体系，虽然这套体系和我们现有理论大相径庭？无论怎样，如果我们当真生活在宗教胜出的那个平行世界中，我们不但不会质疑这个问题，相反还会问自己如果科学战胜了宗教的话生活会变得多么不可思议。因为“科学”的定义变了。
我们到底应该如何获取知识，如何探索世界，在这个根本问题上的分歧形成了不同的“科学范式”。一个科学范式下理所当然的东西在另一个科学范式下可能变得无比荒谬，因为它们在科学发展的最底层就已经有了矛盾。当宗教统治人类历史时，宗教便是“科学”；外人看来再不合理的事情，只要是在自己圈子里发展出来的，怎么看都再正常不过。宗教与科学之争其实是两个科学范式之间的战争，它们的争端永远没有办法解决，因为各自的理论在各自的研究方法之下都是正确的，它们本身并无对错之分，谁也说服不了谁。我们或许期待着有那么一套“算法”作为法官来评判哪个科学范式更好，不幸的是这个法官本身所代表的就是第三种科学范式，争端不但没有任何缓和，反而扩大了。
前几天刚看完《科学哲学》这本书。科学哲学很有意思。这里我举一个有趣例子来说明，科学哲学问题相当值得思考。
《从一到无穷大》选谈：思维的尺度
这个月月初就开始看《从一到无穷大》，花了接近两个星期才看完。这确实是一本让人放不下手的好书。考虑到我的阅读速度，一个多星期一本书已经近乎神速了。在这本书里我经常会看到一些有趣的数学知识，前段时间我还写过书里提到的一个有趣的东西——环面上的染色问题反而比平面上的“四色问题”更加简单。这种例子并不罕见，很多时候一些扩展版的问题反而比原问题更加简单。在第八章，我看到了另一个好玩的东西：随机游走(random walk)问题。
随机游走问题是说，假如你每次随机选择一个方向迈出一个单位的长度，那么n次行动之后你离原点平均有多远（即离原点距离的期望值）。有趣的是，这个问题的二维情况反而比一维情况更加简单，关键就是一维情况下的绝对值符号无法打开来。先拿一维情况来说，多数人第一反应肯定是，平均距离应该是0，因为向左走和向右走的几率是一样的。确实，原点两边的情况是对称的，最终坐标的平均值应该是0才对；但我们这里考虑的是距离，它需要加上一个绝对值的符号，期望显然是一个比0大的数。如果我们做p次实验，那么我们要求的平均距离D就应该是
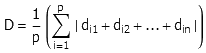
其中d的值随机取1或者-1。这里的绝对值符号是一个打不破的坚冰，它让处于不同绝对值符号内的d值无法互相抵消。但是，当同样的问题扩展到二维时，情况有了很大的改变。我们把每一步的路径投射到X轴和Y轴上，利用勾股定理我们可以求出离原点的距离的平方R^2的值：
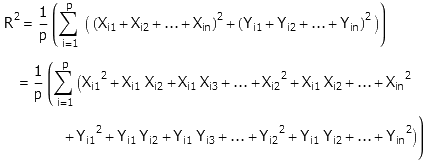
一旦把平方展开后，有趣的事情出现了：这些X值和Y值都是有正有负均匀分布的，因此当实验次数p充分大时，除了那几个平方项以外，其它的都抵消了。最后呢，式子就变成了
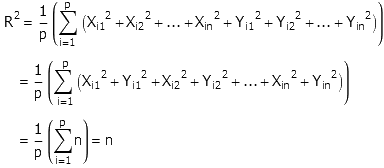
于是呢，就有平均距离R=sqrt(n) （准确的说是均方根距离）。我们得出，在二维平面内随机选择方向走一个单位的长度，则n步之后离出发点的平均距离为根号n。这是一个很美妙的结论。