
照片
假如宇宙是有界的……
看完Proofs from THE BOOK的几何部分,我决定把书又放一放,开始阅读Infinity and the Mind。我承认我不该在当代文学史课上读这本书——读到第15页时,我看到了一段非常有趣的文字,竟然在课堂上放声大笑出来。不知道大家之前是否见过这个“思维实验”,我好像是第一次见到,它真的好搞笑。
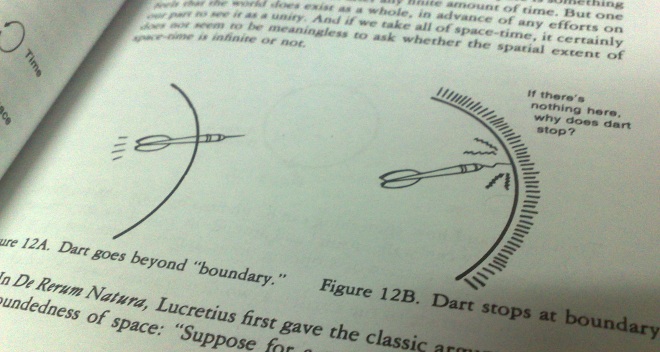
历史上,不同的人对宇宙空间有着不同的见解。古罗马哲学家Lucretius认为,宇宙是无限的。让我们来看一看他的经典论证。假设宇宙是有限的。我们往宇宙的边界投掷一根标枪。则我们将看到以下两种情况之一:这根标枪穿过边界飞向远方,这说明宇宙并无边界,它是无限的;或者这根标枪一头装上宇宙边界停了下来,这说明边界外“有东西”挡住了标枪,同样说明宇宙是无界的。
Update: 其实我想说的是,笑点不是古人的论证与现代科学的差距,而是论证自身用到的二难性所带来的滑稽效果与逻辑推理出奇宏大的力量;正如证明上帝不是万能的(上帝能否创造一块连自己也举不起来的石头),或者大球小球落下去的速度一样快之类的思维实验,它们总是让人会心一笑。
Steffen可活动多面体
大家都知道,三角形具有稳定性。如果你把三根木条钉成一个三角形,则这几根木条是不能活动的。这是因为,根据三角形的SSS全等判定法则,两个三角形的三边长对应相等,则这两个三角形一定全等。但四边形就不是了,用四根一样长的木条钉成一个正方形,握着相对的两个角往两边一拉,正方形就变成菱形了。不知道大家想过没有,类比到三维空间中,多面体的稳定性又是怎样的呢?
Cauchy定理指出,如果两个凸多面体对应的面全等,那么这两个多面体全等。这告诉我们,任何一个凸多面体一定都是不可活动的。在Cauchy定理中,“凸多面体”这一条件是必需的。如果允许凹的多面体存在,对应面相等但整个多面体不全等的形状可以很轻易地构造出来。例如,想象立方体的某个面中心有一个小金字塔,这个金字塔既可以是向外凸的(就像表面上的一根刺),也可以是向内凹的(表面上的一个坑);这是两个截然不同的多面体,但它们的对应面都是相等的。不过,这与我们的稳定性并没有关系,因为它并不是做连续的变形,而是直接一下就“跳”过来了。
很长一段时间,人们曾经猜想,不存在可以做出连续变形且保持所有面不变的“可活动多面体”(Flexible Polyhedron)。1978年,Connelly找到了第一个反例。他给出了一个由18个面组成的可活动多面体。
This is a triumph!
欧拉的一篇研究报告:关于整数因子和的一个非常奇特规律的发现
《数学与猜想》里引用了一段欧拉的这篇经典的研究报告,写的非常精彩。你可以从中看到一个数学家是如何进行发现、归纳、猜想和论证的。你可以看到两个完全不同的数学模型里出现了惊人的巧合,通过挖掘它们之间的内在联系,最终完成了伟大的统一。
没扫描仪,拿相机拍的,效果非常不好,见谅了!
另外,拜托大家不要盗链下面的图片。









