2008-11-17 0:40| 
15 Comments | 本文内容遵从 大家都知道，三角形具有稳定性。如果你把三根木条钉成一个三角形，则这几根木条是不能活动的。这是因为，根据三角形的SSS全等判定法则，两个三角形的三边长对应相等，则这两个三角形一定全等。但四边形就不是了，用四根一样长的木条钉成一个正方形，握着相对的两个角往两边一拉，正方形就变成菱形了。不知道大家想过没有，类比到三维空间中，多面体的稳定性又是怎样的呢？
Cauchy定理指出，如果两个凸多面体对应的面全等，那么这两个多面体全等。这告诉我们，任何一个凸多面体一定都是不可活动的。在Cauchy定理中，“凸多面体”这一条件是必需的。如果允许凹的多面体存在，对应面相等但整个多面体不全等的形状可以很轻易地构造出来。例如，想象立方体的某个面中心有一个小金字塔，这个金字塔既可以是向外凸的（就像表面上的一根刺），也可以是向内凹的（表面上的一个坑）；这是两个截然不同的多面体，但它们的对应面都是相等的。不过，这与我们的稳定性并没有关系，因为它并不是做连续的变形，而是直接一下就“跳”过来了。
很长一段时间，人们曾经猜想，不存在可以做出连续变形且保持所有面不变的“可活动多面体”(Flexible Polyhedron)。1978年，Connelly找到了第一个反例。他给出了一个由18个面组成的可活动多面体。
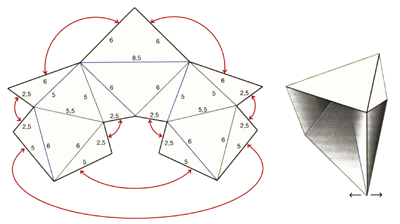
Proofs from THE BOOK的第12章给出了Cauchy定理的一个非常精巧的证明，并在这一章末尾给出了一个更加简单的可活动多面体（上图），它是由Klaus Steffen构造出来的，只含有14个面和9个顶点，现在已经证明是“最简单”的可活动多面体。如果你按图中所标注的比例裁剪一张展开图，拼接成一个多面体的话，你可以捏着它的一条棱拽来拽去的玩。
你猜怎么着？我还就真做了一个！我把这个pdf文件打印在了一张稍微硬一点的纸上，然后按图示粘贴成了一个可活动的多面体。标了黑线的地方应该往外折，蓝线则应该往内折。做好后捏在手里玩了一下，嘿，还真他妈的可以动！
沙发。
我也做成一个
强悍...没打印机的飘过...
这是谁的手
对数学这么感兴趣，在中文系？----8皮 from PKU SMS 05
哈～～手手好可爱～～
nice hand
ORZ地基
Proofs from THE BOOK 你在哪买的啊？
这该怎样证明？
做好后捏在手里玩了一下，嘿，还真他妈的可以动！
感觉是纸在变形啊。
什么时候用铁板销一个，看能不能动。
非常兴奋地发现……M67同学的本本跟我的一模一样……
楼层: 地核 | 2008-11-17 23:10 | Phil 说：
Proofs from THE BOOK 你在哪买的啊？
http://www.amazon.cn/mn/detailApp?ref=YA&uid=168-5304179-1055416&prodid=zjbk481780
大牛 Google 一下 kaleidocycles
wiki 没有
跟你这个有点像，又有点不一样