首先，祝大家情人节快乐。不过，对于单身 Geek 来说，情人节或许并不快乐。情人节可以说是各种 Geek 们永久的伤痛了。即使是热爱数学的你，或许看到已经被转发到烂的“心之函数”今日再度走红，心中也会觉得不爽：我们发明出来的 Geek 玩物，竟然都被你们这些非 Geek 人士拿去装 Geek 泡妞用了，最终情人节宅在家里面向显示器编程度过平凡一天的反而还是我们这群 Geek 。
于是乎，“订完全部大床房”、“买光影院单号位”、“扎破所有安全套”等经典段子年年少不了。当然，我也没有闲着。为什么有 Geek 式的爱情祝福，就没有 Geek 式的分手诅咒？我计划着创作一个“分手函数”，它的函数图像是一个裂成两半的心。
最近看到一类有趣的问题：如何求解 f(f(x)) = g(x) ？我在网上简单搜索了一下，发现这里面真是大有文章。最先对这个问题进行系统研究的应该是 Hellmuth Kneser ，他把函数迭代的次数扩展到了非整数的情况，求解 f(f(x)) = g(x) 就可以更简单地说成是求解 g(x) 迭代 1/2 次后的结果，更形象的说法就是 g(x) 的“平方根”。 Hellmuth Kneser 还对 f(f(x)) = e^x 的解进行了研究，从之后的数学论文发表情况来看，这也是数学家们最关心的问题。
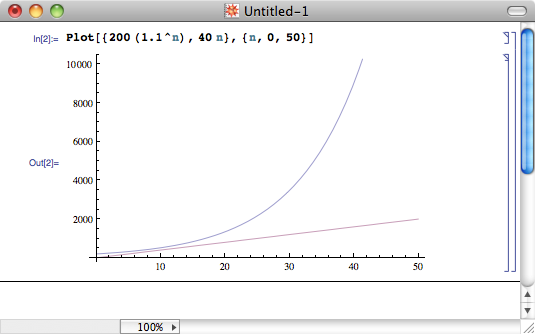
e^x 的“平方根”究竟是什么样的呢？不妨假设满足要求的 f(x) 也是一个连续递增的函数，那么它的增长速度必然超过一切多项式函数（否则迭代的结果还是多项式），同时也必然小于一切指数形式的函数。而事实上，求解一个满足要求的 f(x) 并不难；稍作思考，我们就能够给出一个看似有些平凡的答案。
取任意一个负数，记作 a 。选取任意一个在 (-∞, a] 上单调递增的函数，使得当 x 从 -∞ 增加到 a 时，函数值也从 a 增加到 0 。这样一来，当 x 趋于负无穷时， f(x) 趋于 a ， f(f(a)) 就正好趋于 0 了。但 f(a) = 0 ，那么 f(0) 就必须是 e^a ；而考虑到 f(0) ＝ e^a ，那么 f(e^a) 便只能取 1 了。同理，f(1) = e^(e^a)，而 f(e^(e^a)) 就等于 e 。以此类推，我们便得到了一连串满足要求的点。我们可以从 (-∞, a] 上的其它点出发，用同样的方法填充上述“端点值”之间的部分，得到满足要求的 f(x) 。
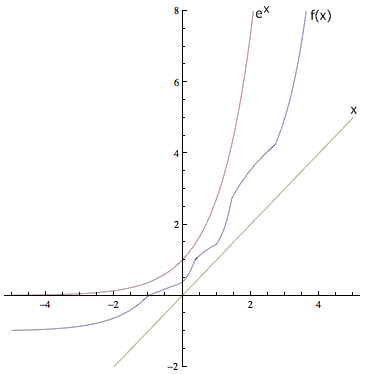
根据这个思想，我们可以构造出一个具体的 f(x) 来。取 a = -1，在 (-∞, -1] 上定义 f(x) = e^(x+1) – 1，它的函数值正好从 -1 变到了 0 。在 (-1, 0] 上，则有 f(x) = e^(f-1(x)) = e^(ln(x + 1) – 1) = (x + 1)/e 。对于其它的 x ，则递归地定义为 f(x) = e^(f(ln(x))) 。由此我们便得到一个分段函数，正是这个分段的办法才让它夹在了多项式增长和指数级增长之间：
最近，一道 Google 校园招聘面试题红遍了整个中文网络：
现在北京有一套房子，价格 200 万，假设房价每年上涨 10% ，一个软件工程师每年固定能赚 40 万。如果他想买这套房子，不贷款，不涨工资，没有其他收入，每年不吃不喝不消费，那么他需要几年才能攒够钱买这套房子？
A. 5年
B. 7年
C. 8年
D. 9年
E. 永远买不起
并不让人感到意外，这道题的答案选 E 。这背后的数学道理就是，线性的增长速度毕竟是赶不上指数级的增长速度的。我用 Mathematica 画了一个简单的图，按照题目所给数据模拟了 50 年内的房价和收入情况。可见，尽管底数仅仅是 1.1 ，指数级增长的威力也一如既往的令人震撼。
唉⋯⋯什么时候工资也能成比地增长就好了。
三年前，我在 Blog 上发了一篇日志，给大家介绍了一个能绘出立体心形的方程，并用 Mathematica 把它画了出来。今年夏天将至， Geek Power 又推出了一系列有创意的衣服，那个著名的“心之函数”也终于走出了电子世界，来到大家的生活之中。在制作这款衣服的印花时，我也算是出了一点力吧，因此 Geek Power 的店主特地送了我一件，看上去效果很不错。