称假币问题的变形：无假币与“天平机”

大家应该听说过 9 枚硬币的问题吧。9 枚硬币当中有 8 枚是真币，有 1 枚是假币。所有的真币重量都相同，假币的重量则稍重一些。怎样利用一架天平两次就找出哪一枚硬币是假币？方法是，先把 9 枚硬币分成三组，每组各 3 枚硬币。然后，把第一组放在天平左边，把第二组放在天平右边。如果天平向左倾斜，说明假币在第一组里；如果天平向右倾斜，说明假币在第二组里；如果天平平衡，说明假币在剩下的第三组里。现在，假币的嫌疑范围就被缩小到 3 枚硬币之中了。选择其中 2 枚硬币分放在天平左右两侧。类似地，如果天平左倾，就说明左边那枚硬币是假的；如果天平右倾，就说明右边那枚硬币是假的；如果天平平衡，就说明没放上去的那枚硬币是假的。

9 硬币问题实在是太经典了，你甚至能在人教版小学五年级下册的课本里看到它。9 硬币问题还衍生出了很多变形，其中最著名的当属 12 硬币问题了：有 12 枚硬币，其中一枚是假币，但我们不知道假币是更重一些还是更轻一些；请利用一架天平三次找出哪一枚硬币是假币，并判断出它比真币更重还是更轻。12 硬币问题的经典程度恐怕不亚于 9 硬币问题。早在 20 世纪 40 年代，12 硬币问题就已经吸引了一大批数学家和数学爱好者，甚至有人建议把这个问题扔到德国去，以削弱德国人在二战中的战斗力。如果你想知道答案，可以在网上找找，应该很容易找到。我们今天就不讨论了。

今天，我们真正想聊的其实是这个问题的另外一种比较少见的变形：仍然是要在 9 枚硬币当中寻找 1 枚假币，仍然假设假币的重量要稍重一些，仍然只能使用天平两次；但是这一次，你所使用的是一种“天平机”，它不会立即告诉你现在是哪边重哪边轻，而是在你两次称完后把这两次的结果一并打印给你。这下，你就没法根据天平的反馈结果随机应变了，必须事先把每次怎么放硬币全规划好。那么，你该怎么办？在本文后面的内容中，均已知假币比真币更重，直至另有说明。

答案并不复杂。你的第一步应该和刚才一样，仍然是把 9 枚硬币均分成三组，把第一组放在天平左边，把第二组放在天平右边。妙就妙在第二步。我们的原计划是，哪一组里有假币，就在哪一组里选出 2 枚硬币分放在天平两侧。但是，由于没有及时的反馈，我们根本就不知道哪一组里有假币，这该怎么办呢？其实，我们根本不用管哪一组里有假币，从每一组里都选 2 枚硬币放上去就行了，反正另外两组硬币都是真的，放上去了不会有什么影响。这有一点“并行运算”的意思。举例来说，如果第一步放在天平左右两侧的硬币编号分别是 1、2、3 和 4、5、6，那么第二步放在天平左右两侧的硬币编号就应该是 1、4、7 和 2、5、8。如果事后天平告诉我，第一次称完左边更重一些，那么我就知道了假币一定在 1、2、3 当中，于是第二次左边更重就说明 1 是假币，第二次右边更重就说明 2 是假币，第二次天平平衡就说明 3 是假币，而第二次天平上的 4、7、5、8 其实都是来“陪称”的。

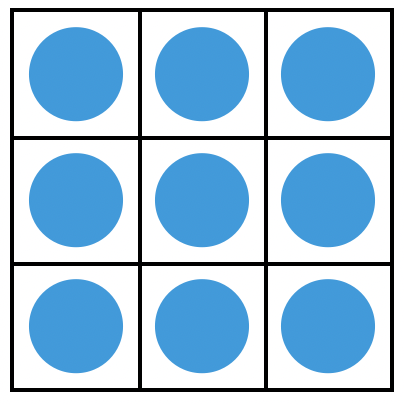
在给别人讲这个解法时，我更喜欢用下面这种等价的但更为直观的叙述方法：把 9 枚硬币摆成三行三列。在第一轮里，我们把第一行的硬币放到天平左边去，把第二行的硬币放到天平右边去；在第二轮里，我们把第一列的硬币放到天平左边去，把第二列的硬币放到天平右边去。之后，天平将把这两轮称重的结果告诉我们，本质上就相当于告诉了我们假币在第几行第几列，于是我们就能锁定假币的编号了。这段内容特别适合讲给小学五年级和初中一年级的学生，因为他们会发现，刚学的用数对表示位置的知识居然在这里派上了用场。

聊完 9 硬币问题的“天平机”变形后，让我们再来聊一种新的变形：可能没假币。9 枚硬币当中可能有 1 枚的假币，也有可能根本就没有假币。怎样利用一架天平两次就找出假币（如果有的话），或者确定出所有的硬币都是真币？

听完这个问题，你的第一反应是什么？你的第一反应或许是——这怎么可能有解呢？觉得此题无解，背后其实是有一些直觉的——原始 9 硬币问题的解法已经发挥到极致了，再多一点不确定的因素，恐怕就没有额外的手段来处理它了。这个直觉是对的。我们可以把这个直觉转化成更加严谨的语言。

每称一次硬币，天平都会产生三种不同的状态：向左倾斜，向右倾斜，保持平衡。接下来究竟该怎么做，取决于天平产生的状态。形象地说，此处会产生三个不同的分支剧情。在每一种分支剧情下，我们都会再使用一次天平，进而又产生三个小分支剧情。由于我们一共就只能使用两次天平，因此我们一共能得到 3 × 3 = 9 个不同的结局。若 9 枚硬币中一定有 1 枚假币，则一共有 9 种要分辨的情况：1 号硬币是假币，2 号硬币是假币，一直到 9 号硬币是假币。9 个不同的结局，正好分别对应 9 种不同的情况。然而，如果 9 枚硬币中可能有 1 枚假币，则一共有 10 种要分辨的情况：1 号硬币是假币，2 号硬币是假币，一直到 9 号硬币是假币，以及没有假币。9 个不同的结局，容纳不下 10 种不同的情况。至少有一个结局会同时对应两种或两种以上的情况，它们就无法被区分开来了。

上面的理论告诉我们，如果不确定有没有假币，并且只能用两次天平，顶多只能解决有 8 枚硬币的情况。那么，当硬币数为 8 的时候，问题实际上有没有解呢？有！而且方法并不难，很好想。把 8 枚硬币分为三组，前面两组都是 3 枚，第三组是 2 枚。把第一组和第二组分别放在天平的左右两边。接下来会产生两个分支剧情：

如果天平不平衡，说明假币一定有，并且在较重的那一组当中。再称一次，就能把这一组中哪一枚硬币是假币给称出来。
如果天平平衡，说明假币要么在第三组，要么不存在。将天平清空，把第三组的两枚硬币分别放在天平两边，哪边重就说明假币在哪边，一样重就说明假币不存在。

现在，我们讲了 9 硬币问题的两种变形：“天平机”变形，和“可能没假币”变形。但经过探究，我们发现后者最多只能解决 8 枚硬币的情形。或许你认为这篇文章快结束了吧。现在，好戏才刚刚开始。我们把刚才的两种变形结合在一起，构造一个真正的难题：你只能使用“天平机”，而且有可能没假币，请你用两次天平找出假币（或确定假币不存在）。在“可能没假币”的变形中，即使不加“天平机”变形，最多也只能解决 8 硬币问题；所以，在两种变形叠加的情况下，8 硬币也是一个上限。因而，我们把总硬币的数量设为 8。

8 枚硬币，可能没假币，用“天平机”，能搞定吗？在出现了“天平机”这样的玩意儿时，最直观而有效的分析方法还是之前的 3 × 3 方阵。事实上，两次“天平机”应该怎么用的问题，完全等价于方阵里的硬币应该怎么摆的问题。每次使用天平时，要决定的无非就是左边放哪些硬币，右边放哪些硬币；而在“天平机”的假设下，第一轮决定和第二轮决定是互相独立的。所以，设计一套解决问题的方案，无非就是为每一枚硬币指定去处：第一次是放左边、放右边还是不上天平，第二次又是放左边、放右边还是不上天平。这一切都可以借用 3 × 3 的方阵陈列出来。第一行第二列里的硬币，就是第一次放左边，第二次放右边的硬币；第二行第三列里的硬币，就是第一次放右边，第二次不上天平的硬币。

在摆放硬币时，有一个非常基本的原则：每个格子里最多只能放一枚硬币。这是因为，如果某个格子里放了两枚甚至更多枚硬币，说明它们自始至终一直是“捆绑”在一起的，如果其中一枚硬币是假币，我们就没法区别了。之前有 9 枚硬币，正好摆满整个方阵；这次只有 8 枚硬币，没法把方阵填满了。我们只好把它们摆成这样了：

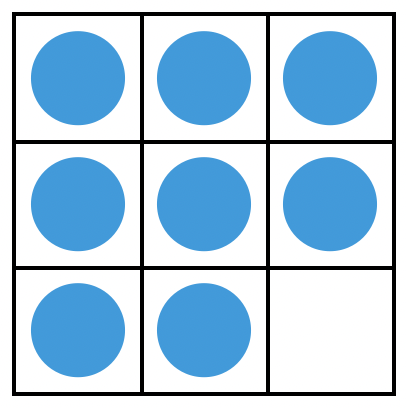
嘿，这样也就搞定了。先把头两行的硬币分别放在天平左右两边，第三行硬币不放上去，我们就能知道假币在哪一行；再把头两列的硬币分别放在天平左右两边，第三列硬币不放上去，我们就能知道假币在哪一列。如果天平两次都平衡，说明硬币既不在头两行，也不在头两列；然而这样的硬币根本不存在，因而可以断定此时没有假币。

不管是用普通天平还是用“天平机”，8 枚硬币中可能有 1 枚假币的情况，已经蕴含了 8 枚硬币中一定有 1 枚假币的情况。可能有 1 枚假币时的解法，能直接套用于一定有 1 枚假币的情况，无非就是某种小概率事件永远不会发生罢了。

至此，我们讨论了 9 硬币问题的 8 个具体变形：

9 枚硬币，一定有假币，用普通天平
9 枚硬币，一定有假币，用“天平机”
9 枚硬币，可能没假币，用普通天平（无解）
9 枚硬币，可能没假币，用“天平机”（无解）
8 枚硬币，一定有假币，用普通天平
8 枚硬币，一定有假币，用“天平机”
8 枚硬币，可能没假币，用普通天平
8 枚硬币，可能没假币，用“天平机”

接下去，我们是不是应该开始研究下面四个问题了？

7 枚硬币，一定有假币，用普通天平
7 枚硬币，一定有假币，用“天平机”
7 枚硬币，可能没假币，用普通天平
7 枚硬币，可能没假币，用“天平机”

此时，我似乎听见了读者们的大笑声：只见过有些题目里往上讨论越来越大的 n，还从没见过什么题目里往下讨论越来越小的 n。呵呵，谁说 n 越大题目越难了？如何把一个正方形分成 9 个小正方形，这个问题的答案大家肯定能立即想到；如何把一个正方形分成 8 个小正方形，这个事儿恐怕很多人没法立即想到答案吧！

类似地，7 硬币问题也有它的特殊之处，使得从某种意义上它更难一些。不管是一定有假币的情况，还是可能没假币的情况，用普通天平倒是很快能解决。把 7 枚硬币分为三组，前面两组都是 3 枚，第三组是 1 枚。把第一组和第二组分别放在天平的左右两边。接下来会产生两个分支剧情：

如果天平不平衡，说明假币一定有，并且在较重的那一组当中。再称一次，就能把这一组中哪一枚硬币是假币给称出来。
如果天平平衡，那就说明前两组硬币肯定都是真的。从中拿其中一枚真币去跟第三组的那枚硬币比轻重，就知道第三组的那枚硬币是真是假了。

麻烦的还是用“天平机”的情况。我们先考虑一定有假币的情况。是不是仿照刚才的例子，只需要把 7 枚硬币摆成这样就行了呢？

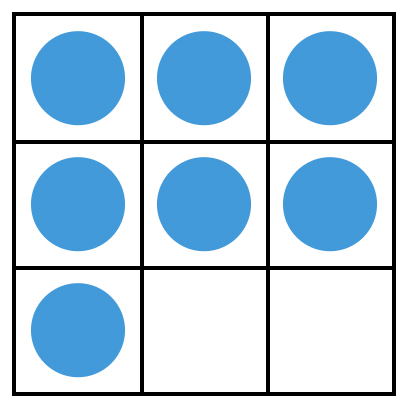
这次就不行了。虽然把前两行的硬币分放天平的左右两边，可以知道假币在三行中的哪一行，但把前两列的硬币分放天平的左右两边，无法知道假币在三列中的哪一列。这是因为，前两列的硬币个数不一样，其中一枚硬币较重，不见得会让它所在的这边下沉。所以，摆放硬币时，我们还得让前两行的硬币数相同，并且前两列的硬币数也相同。比方说，我们摆成这样：

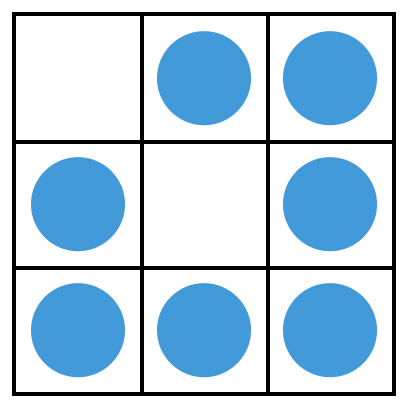
这样就能用“天平机”两次解决问题了，不管是一定有假币的情况，还是可能没假币的情况。呃……是吗？

事实上，7 枚硬币，可能没假币，用“天平机”，这种情况是使用两次天平无法解决的。最为关键的一点就是，和必然有假币的情况不同，在可能不存在假币的情况下，每一枚硬币都得有至少一次要上秤。这是为什么呢？道理很简单。假设我们打算把某一枚硬币丢在一边，每次都不上秤，那我们无法区别“假币就是这枚硬币”和“假币不存在”这两种可能性。这说明，把硬币摆进 3 × 3 的方阵时，最右下角的那个格子里是不能放硬币的。

在 3 × 3 的方阵里，除掉最右下角的格子，还剩下 8 个格子。如果要在里面放 7 枚硬币，那就恰好有 1 个格子是空的。不管空的格子是这 8 个格子中的哪一个，都会使得前两行的硬币数不一样，或者前两列的硬币数不一样。然而，在每次称硬币的时候，两边放的硬币数必须得相同，不然没有任何意义。这就说明，用“天平机” 2 次称出 7 枚硬币中的假币，在假币可能不存在的假设下，是无法办到的。

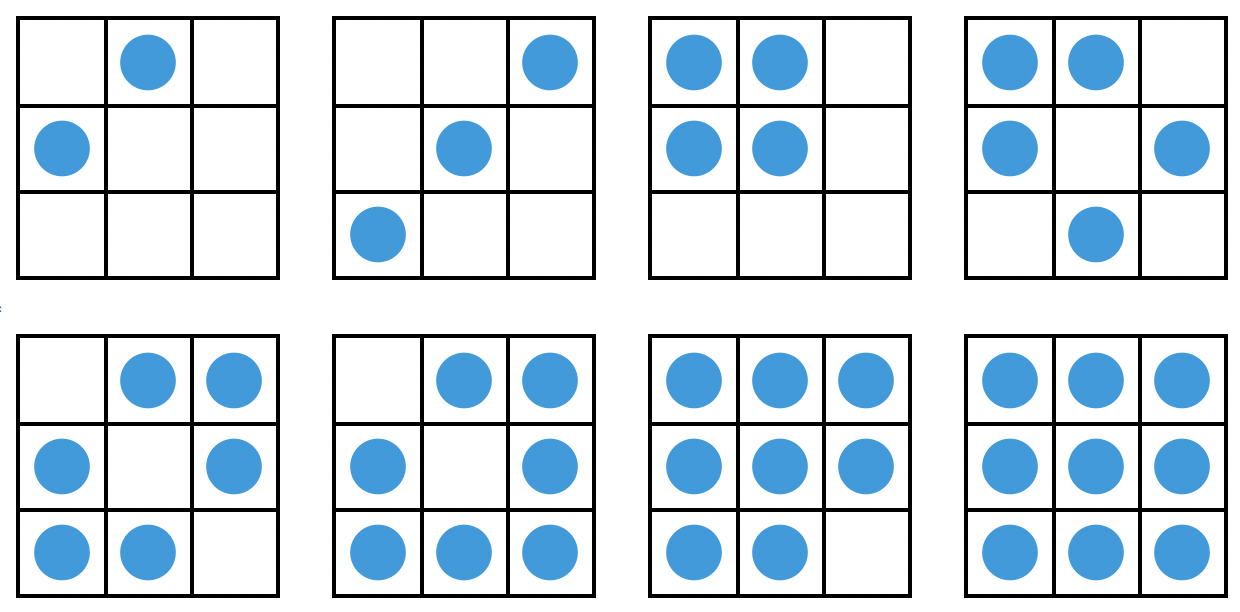
利用硬币方阵研究此类问题能够起到事半功倍的效果。上面的硬币方阵图告诉我们，在“天平机”变形中，使用两次“天平机”，可以找出 2、3、4、5、6、7、8、9 枚硬币中的一枚假币（如果假币一定存在），虽然 2 枚硬币和 3 枚硬币的情况显然用一次“天平机”就够了；也可以找出 2、3、4、5、6、8 枚硬币中的一枚假币（如果假币不一定存在），虽然 2 枚硬币的情况显然用一次“天平机”就够了。这是因为，这些图都满足：

每个格子里最多放一枚硬币
第一行和第二行的硬币数相同
第一列和第二列的硬币数相同
对于可能没假币的情况，最右下角的格子里没有硬币

两次使用“天平机”究竟能办到哪些事情，就被我们彻底分析清楚了。

当然，数学研究过程中的欲望永远是无止境的。我们接下来就想问：三次使用“天平机”能办到哪些事情？大家或许会作出下面这几个看起来非常合理的猜测：

一定有假币时，三次使用“天平机”除了能够解决两次使用“天平机”就能解决的问题以外，还能够解决 10 到 27 枚硬币的情况。
可能没假币时，三次使用“天平机”除了能够解决两次使用“天平机”就能解决的问题以外，还能够解决 9 到 26 枚（但不含 25 枚）硬币的情况。
可能没假币时，之前两次使用“天平机”不能解决的 7 硬币情形，三次使用“天平机”应该足够了。
可能没假币时，现在三次使用“天平机”不能解决的 25 硬币情形，恐怕得四次使用“天平机”才够。

这些猜测显然参考了普通天平情况下的结论推广模式。这是数学归纳法的经典应用。我们简单地做个回顾。我们来证明，n 枚硬币中一定有一枚假币，要用 k 次普通天平找出这枚假币，则问题有解的充分必要条件是 n ≤ 3^k。

必要性很容易说明，其核心思路本文一开始就已经说过了：每使用一次天平，会产生三个分支剧情；使用 k 次天平，一共会产生 3^k 个不同的结局。这只够区分 3^k 个不同的可能性。然而，究竟谁是假币，这一共有 n 种不同的可能性。所以，n 不能超过 3^k。

为了证明充分性，我们只需要给出一种方案即可。数学归纳法就派上用场了。当 k = 1 时，结论显然成立。我们现在要把更大的 k 归结为 k − 1 时的情形。我们的基本策略就是，先把硬币分成三组，并且前两组硬币一样多。把前两组硬币放上天平，根据天平状态便能得知假币在哪一组。如果不管假币在哪一组，接下来都能用 k − 1 次天平找出假币就好了。这意味着，每组硬币的数量都不能超过 3^k−1。因此，我们要做的无非就是，把一个不超过 3^k 的数 n，分解成三个不超过 3^k−1 的数之和，并且前两个数相等。由于 n ≤ 3^k，因此 n÷3 ≤ 3^k−1。接下来分三种情况讨论。

如果 n÷3 正好是个整数，直接把 n 分成 n/3, n/3, n/3 就行了
如果 n÷3 等于某个整数又 1/3，那就把 n 分成 n/3 − 1/3, n/3 − 1/3, n/3 + 2/3
如果 n÷3 等于某个整数又 2/3，那就把 n 分成 n/3 +1/3, n/3 + 1/3, n/3 − 2/3

容易验证，这些情况下的分法都满足要求。

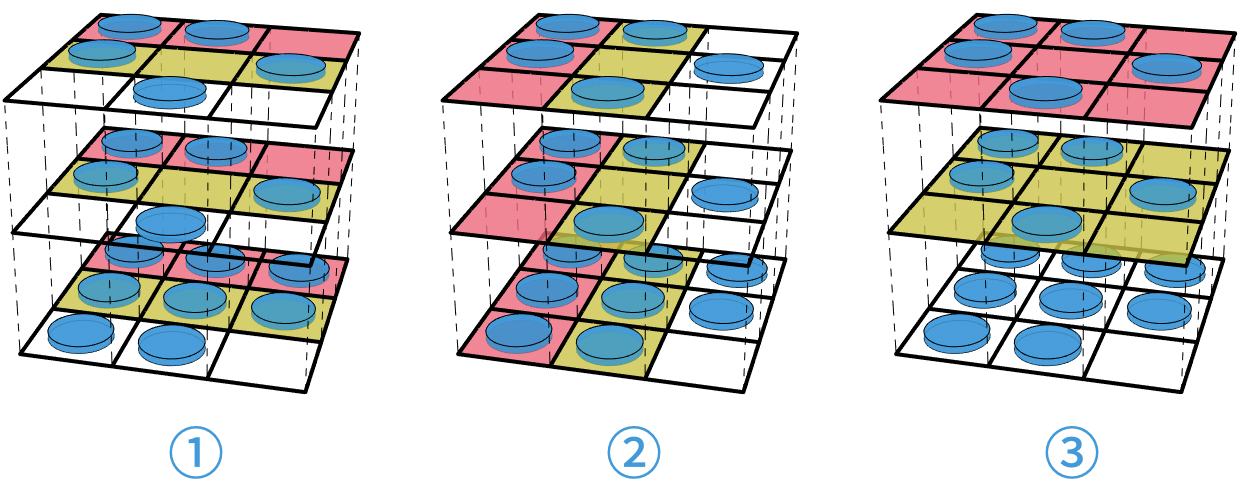
如何对“天平机”情况下的结论进行推广呢？如果说两次使用“天平机”时的最佳分析工具是 3 × 3 方阵，那三次使用“天平机”时就得使用 3 × 3 × 3 的立方阵了。让我们把硬币放进立方阵。

接下来，按照下面的原则完成后续操作。

把由远至近第一个纵切片（图 1 中的红色部分）里的所有硬币放在天平左边，把由远至近第二个纵切片（图 1 中的黄色部分）里的所有硬币放在天平右边。
把从左到右第一个纵切片（图 2 中的红色部分）里的所有硬币放在天平左边，把从左到右第二个纵切片（图 2 中的黄色部分）里的所有硬币放在天平右边。
把从上往下数第一层（图 3 中的红色部分）里的所有硬币放在天平左边，把从上往下数第二层（图 3 中的黄色部分）里的所有硬币放在天平右边。

如果每次放在天平两边的硬币个数相同，我们就能确定假币的三维空间坐标，谁是假币就立即揭晓了。问题就是，怎样摆放硬币，才能使得每次放在天平两边的硬币个数相同。换句话说，我们需要各个方向上的第一个切片和第二个切片都拥有相同数量的硬币。

普通天平的推广充分用到了数学归纳法，“天平机”变形的推广多半也跟数学归纳法脱不了干系。所以，在搭建符合要求的立体方阵时，我们可以想办法把之前那些符合要求的平面方阵给用上。比方说，我们可以让立方阵中从上往下的每一层都是一个符合要求的 3 × 3 硬币方阵图。这样一来，不管是在图 1 中，还是在图 2 中，每一层的红色部分和黄色部分都有相同数量的硬币，整个红色纵切片和整个黄色纵切片也就拥有相同数量的硬币了。为了让前两层里的硬币数也一样多，我们可以额外地要求，前两层必须是完全相同的 3 × 3 硬币方阵图。前面的图示中给出的，就是 18 枚硬币时一个符合要求的立体方阵。

但是，如果要把结论进一步推广到四次使用“天平机”，我们又该怎么办呢？难道真的要把三维方阵继续升级成四维方阵？不用。描述高维空间的其中一种方法就是用直角坐标系，比如四维空间中的点就与四个坐标值形成的四元组相对应。而在我们的问题中，每个维度就只有三种可能的坐标值：放左边、放右边、不放上去。我们不妨依次用 L、R、0 表示它们。我们可以用这种方式把每个小球在高维空间中的位置表示出来，哪怕是 100 维、1000 维的空间。其实，我们并不是开创了新的分析方法，而仅仅是回归到了问题的本源。一枚硬币各次的去处，本来就该用这么一串记号来表示；图形化的分析方法，则起到了一个参谋的作用。

如果硬币一共有 n 枚，“天平机”可以使用 k 次，那么所有硬币的各次去向可以整理成下面这样的形式：

C₁ = (L, L, L, …, L)
C₂ = (R, L, L, …, L)
C₃ = (0, L, L, …, L)
……
C_n = (0, 0, 0, …, 0)

这个表格需要满足：

任意两行都不能完全相同
每一列中 L 和 R 的个数相同
对于可能没假币的情况，不能有某一行全是 0

设计称币方案的问题，就转化为了编排表格的问题。受之前的图形化分析结果的启发，我们有了下面的核心策略。如果硬币一共有 n 枚，“天平机”可以使用 k 次，我们就把 n 拆成 n₁ × 2 + n₂，使得硬币有 n₁ 枚或者 n₂ 的情况下，使用 k − 1 次或更少次数的天平都能完成任务。然后，我们把两张 n₁ 枚 k − 1 次的表格和一张 n₂ 枚 k − 1 次的表格接在一起，组成一个有 n 行 k − 1 列的大表格（不足 k − 1 列的地方用 0 补足），再给前 n₁ 行的最末尾添一个 L，给接下来 n₁ 行的最末尾添一个 R，给最后 n₂ 行的最末尾添一个 0。这就得到了一个 n 枚 k 次时符合要求的表格。这是因为：

每个小表格内部都没有重复的行，而来自不同表格的行又拥有不同的“后缀”，因而大表格中的任意两行都不重复。
根据构造方法，第 k 列的 L、R 个数相等。对于前面 k − 1 列中的任意一列，每个小表格的 L、R 个数都相等，那么合成的大表格显然也满足，该列的 L、R 个数相等。
对于可能没假币的情况，每个小表格里都不会出现某一行全是 0 的情况，整个大表格里也自然不会出现某一行全是 0 的情况。

我们只剩一件事情要做：如何把 n 拆成 n₁ × 2 + n₂。

对于一定有假币的情况，我们的猜想是：当 n ≤ 3^k 时，使用最多 k 次“天平机”就能完成任务。因此，我们需要把 3^k 以内的数，分解成三个 3^k−1 以内的数之和，其中前两个数必须得相等。这件事情我们刚才已经做过一遍了。我把前面的文字原封不动地复制粘贴过来。如果 n ≤ 3^k，那么 n÷3 ≤ 3^k−1。

如果 n÷3 正好是个整数，直接把 n 分成 n/3, n/3, n/3 就行了
如果 n÷3 等于某个整数又 1/3，那就把 n 分成 n/3 − 1/3, n/3 − 1/3, n/3 + 2/3
如果 n÷3 等于某个整数又 2/3，那就把 n 分成 n/3 +1/3, n/3 + 1/3, n/3 − 2/3

对于可能没假币的情况，我们的猜想是：当 n ≤ 3^k − 1 且 n ≠ 3^k − 2 时，使用最多 k 次“天平机”就能完成任务。因此，我们需要把 3^k − 1 以内且不为 3^k − 2 的数，分解成三个 3^k−1 − 1 以内且不为 3^k−1 − 2 的数之和，其中前两个数必须得相等。事实上，前两个数正好都等于 3^k−1 或者都等于 3^k−1 − 2 是没有关系的，因为前两个小表格可以使用一定有假币时的表格。反正最后我们会在这些行的最后面补一个 L 或者 R，即使这些行中有某一行原来全是 0，也不会破坏掉大表格的性质。分解的思路与刚才相同。如果 n ≤ 3^k − 1且 n ≠ 3^k − 2，那么 n÷3 ≤ 3^k−1 − 1/3 且 n÷3 ≠ 3^k−1 − 2/3。接下来分三种情况讨论。

如果 n÷3 正好是个整数，直接把 n 分成 n/3, n/3, n/3 就行了
如果 n÷3 等于某个整数又 1/3，那就把 n 分成 n/3 − 1/3, n/3 − 1/3, n/3 + 2/3
如果 n÷3 等于某个整数又 2/3，那就把 n 分成 n/3 + 1/3, n/3 + 1/3, n/3 − 2/3

这一回，有三个地方会出问题：

如果 n/3 正好等于 3^k−1 − 2，即 n 正好等于 3^k − 6，第一种情况就出问题了。此时，我们只需要把它分成 (3^k−1 − 1) × 2 + (3^k−1 − 4) 就行了。
如果 n/3 + 2/3 正好等于 3^k−1 − 2，即 n 正好等于 3^k − 8 ，第二种情况就出问题了。此时，我们只需要把它分成 (3^k−1 − 2) × 2 + (3^k−1 − 4) 就行了。
如果 n/3 − 2/3 正好等于 3^k−1 − 2，即 n 正好等于 3^k − 4 ，第三种情况就出问题了。此时，我们只需要把它分成 (3^k−1) × 2 + (3^k−1 − 4) 就行了。

至此，我们就完整地给出了各种“天平机”情况下的最优解。

等等……这些解真的是最优的吗？利用前面提过的思路，很容易证明，对于一定有假币的情况，当 n > 3^k 时问题无解，并且对于可能没假币的情况，当 n > 3^k − 1 时问题无解。现在我们要证明，对于可能没假币的情况，n = 3^k − 2 确实无解。回想一下对于可能没假币的情况，表格

C₁ = (L, L, L, …, L)
C₂ = (R, L, L, …, L)
C₃ = (0, L, L, …, L)
……
C_n = (0, 0, 0, …, 0)

需要满足的要求：

任意两行都不能完全相同
每一列中 L 和 R 的个数相同
不能有某一行全是 0

当 n = 3^k − 2 时，上述条件确实无法全部实现。我们来证明这一点。首先，表格的每一行里都有 k 个格子，每个格子里都只能填 L、R、0 之一，因此每一行的填法一共有 3^k 种不同的组合。容易看出，对于任意一个特定的格子，其中 1/3 的组合在该格子里面填了 L，另外 1/3 的组合在该格子里面填了 R，剩下 1/3 的组合在该格子里面填了 0。所以，把这 3^k 种填法组合全列出来，将会满足每一列中的 L 和 R 的个数相同。除去不允许出现的 (0, 0, 0, …, 0) 以外，还有 3^k − 1 种不同的组合。把这 3^k − 1 种填法组合全列出来，仍然满足每一列中的 L 和 R 的个数相同。表格一共有 3^k − 2 行，但填法有 3^k − 1 种组合，所以我们要从中去掉一种组合。在这种组合中，至少有一个格子里填了 L 或者 R 。把该行去掉后，这个格子所在列的 L 和 R 的个数将会失衡。这就说明了，当 n = 3^k − 2 时，满足要求的表格是不存在的。

总结一下目前我们得到的所有结果。在有 n 枚硬币，使用 k 次天平的情况下，问题有解的充分必要条件为：

一定有假币，用普通天平： n ≤ 3^k
一定有假币，用“天平机”： n ≤ 3^k
可能没假币，用普通天平：………………？
可能没假币，用“天平机”：n ≤ 3^k − 1 且 n ≠ 3^k − 2

那么，可能没假币，用普通天平呢？容易想到，“天平机”是更加严苛的要求，所以用“天平机”能解决的，用普通天平当然也能解决。你只需要假装普通天平的前 k − 1 次称量结果并未立即给出，它就变成“天平机”了。另外，在可能没假币的情况下，即使用普通天平，n > 3^k − 1 肯定也是无解的。比较关键的问题就是，普通天平能不能解决 n = 3^k − 2 的情况。答案是肯定的。还记不记得，最开始的 7 硬币问题是怎么解决的？我复制粘贴过来。

类似地，7 硬币问题也有它的特殊之处，使得从某种意义上它更难一些。不管是一定有假币的情况，还是可能没假币的情况，用普通天平倒是很快能解决。把 7 枚硬币分为三组，前面两组都是 3 枚，第三组是 1 枚。把第一组和第二组分别放在天平的左右两边。接下来会产生两个分支剧情。
如果天平不平衡，说明假币一定有，并且在较重的那一组当中。再称一次，就能把这一组中哪一枚硬币是假币给称出来。
如果天平平衡，那就说明前两组硬币肯定都是真的。从中拿其中一枚真币去跟第三组的那枚硬币比轻重，就知道第三组的那枚硬币是真是假了

仿照这个思路，我们有了下面的方案。把 3^k − 2 枚硬币分成 3^k−1, 3^k−1, 3^k−1 − 2 这么三组，并把前两组放到天平的左右两边。如果天平不平衡，说明假币一定有，并且在较重的那一组当中。现在的情况就变成了，其中 3^k−1 枚硬币中一定有 1 枚假币，而这样的情况我们是能用 k − 1 次天平解决的。如果天平平衡，那就说明前两组硬币肯定都是真的，假币要么在第三组里，要么就根本没有。我们从前两组里借来一枚硬币，并入第三组，第三组里就有 3^k−1 − 1 枚硬币了，其中可能有 1 枚假币，可能没有假币，而这种情况也能用 k − 1 次天平解决。所以，我们可以补全上面的列表中缺失的行了：

可能没假币，用普通天平：n ≤ 3^k − 1

最后还要注意的就是，在可能没假币的情况下，我们需要假设 n ≥ 2，否则问题永远无解。至此，我们终于完整地解答了称硬币问题中与无假币和“天平机”相关的所有变形。

其实，我们今天所讨论的仅仅是各种称硬币问题变形的冰山一角。称硬币问题的变形可谓是无奇不有。为了展示这一点，也为了满足部分或许仍然意犹未尽的读者，我们最后以三个古怪而有趣的称硬币问题，来结束今天的全部讨论吧。注意，接下来的假币就不见得更重一些了，大家阅读时稍微留心一下。

问题1

有 100 枚硬币，里面有 99 枚是真币，有 1 枚是假币。所有的真币重量都相同，假币的重量则稍有差异，但你不知道是偏重了还是偏轻了。每一次，你可以选择任意数量的硬币，把其中一些放在天平的左边，把另外一些放在天平的右边，然后观察天平是左偏、右偏还是平衡。想办法只称两次来判断假币是偏轻的还是偏重的（你不需要把假币找出来）。

答案

首先，选 49 枚硬币放在天平左边，再选 49 枚硬币放在天平右边。如果天平是平衡的，那么目前天平上的所有硬币都是真的，假币一定在剩下的 2 枚硬币之中。把这 2 枚硬币放在天平左边，再选 2 枚硬币放在天平右边，如果左边重就说明假币是偏重的，如果左边轻就说明假币是偏轻的。

如果第一次称重的结果是不平衡的呢？这说明现在天平上的所有硬币当中有 1 枚是假币，没放上天平的 2 枚硬币则都是真币。接下来，取出较轻一侧的 49 枚硬币，往里面放入 1 枚真币，于是得到了 50 枚硬币。把这 50 枚硬币分成相等的两组，分别放在天平的两侧。如果天平平衡，说明假币在刚才偏重的那 49 枚硬币当中，从而说明假币是偏重的；如果天平倾斜了，就说明假币就在刚才偏轻的这 49 枚硬币当中，从而说明假币是偏轻的。

显然，只称一次是不可能完成任务的，因此上述方案已经达到最优，不能再改进了。

问题2

你有 14 枚硬币，其中 7 枚是真币，重量都是 10 克，另外 7 枚是假币，重量都是 9.99 克。你不知道哪些硬币是真币，哪些硬币是假币，即使人为鉴定也没法把它们区分开来。好在，你有一个无比精确的天平机器人。每一次，你可以选择任意数量的硬币，把其中一些放在天平的左边，把另外一些放在天平的右边，然后按动按钮。如果两边的总重量相同，天平机器人会如实反馈，并且归还所有的硬币；如果一边重一边轻的话，天平机器人会从重的那边随机选择一枚硬币吃掉，把剩下的硬币归还给你，然后告诉你刚才是哪边更重一些。想一种策略可以保证你从这些硬币中确定出一枚真的（并且没有被吃掉的）硬币。你可以无限制地使用这台天平机器人。

答案

从中选择 4 枚硬币，把它们分成两组，分别放在天平的两侧。如果机器人告诉你天平两侧一样重，那么重新选择 4 枚硬币并且把它们分成两组放上去，直到天平两侧的重量不相等为止。不妨把较轻一侧的两枚硬币叫做 A、B，把较重一侧的两枚硬币叫做 C、D。机器人会从重的那一边吃掉一枚硬币，无妨假设是 D，然后把剩下的 A、B、C 这 3 枚硬币还给你。接下来，把 A、B 这 2 枚硬币分别放在天平左右。如果天平倾斜的话，这说明 A、B 这 2 枚硬币是一真一假的，从而说明刚才的 C、D 都是真的。虽然 D 被吃掉了，但是 C 还在，于是你就得到了一枚还没被吃掉的真币。

如果天平两侧一样重的话，怎么办呢？这说明 A、B 两枚硬币都是假的。现在，把这两枚硬币扔掉，于是总共 14 枚硬币就只剩下 11 枚硬币了。这 11 枚硬币当中，真的肯定要多一些，假的肯定要少一些（实际上，有可能是 7 枚真币 4 枚假币，也有可能是 6 枚真币 5 枚假币，这取决于第一次实验时机器人吃掉的是哪种硬币）。接下来就简单了，不断地把两枚硬币分放天平两侧，直到天平两侧重量不等为止。那么，重的那一侧就是真币，可惜会被吃掉；轻的那一侧就是假币，你可以把它扔掉。这样下来，手中的硬币就少了一枚真的，少了一枚假的，剩下的硬币仍然是真的多假的少。不断这样做下去，手中的硬币越来越少，但真的硬币始终会更多一些。什么时候手里只剩下一枚硬币了，或者手中的所有硬币的重量两两相等时，就说明手里这些硬币都是真的了。

这个问题选自 2011 年 USAMTS 的问题。

问题3

有 9 枚硬币，其中 8 枚是真币，只有 1 枚是假币。所有真币都一样重，假币则稍轻一些。同时，你还有三架天平，其中两架天平是好的，另外一架天平是坏的（但你不知道哪两架是好的，哪一架是坏的）。好的天平总会给出正确的称量结果，但坏的天平会随机给出称量结果。如何使用 4 次天平，保证找出那枚假币？

答案

把硬币摆成三行三列。把第一行的硬币和第二行的硬币分别放在第一架天平的左边和右边，把第一列的硬币和第二列的硬币分别放在第二架天平的左边和右边。如果这两架天平都是好的，我们就知道了假币在哪一行，以及假币在哪一列。无妨假设前两架天平给出的结果表明，假币在第一行第一列。但是，这两架天平究竟是不是都是好的呢？为此，我们将在第一行不在第一列里的硬币（共 2 枚）放在第三架天平的左边，将在第一列不在第一行里的硬币（共 2 枚）放在第三架天平的右边。如果第三架天平平衡，那么假币就只可能是第一行第一列的那枚硬币了（否则至少两架天平的结果与实际情况不符），任务就完成了。如果第三架天平不平衡呢？若左边更轻，则第三架天平的结果与第二架天平的结果相冲突；若右边更轻，则第三架天平的结果与第一架天平的结果相冲突。不管是哪种情况，我们都知道了哪架天平肯定是好的。这架天平刚才已经用过一次了，根据这次的结果，我们已经知道哪 3 枚硬币是假币了。用这架天平再称一次，任务就完成了。

刚才提到，“无妨假设前两架天平给出的结果表明假币在第一行第一列”，这里的“无妨”其实没有那么“无妨”。大家可以稍微留意一下假币实际上在第三行或者第三列的情况，虽然本质相同，但是细节还是稍微有些区别。这个问题来自 2008 年 All−Russian Olympiad 试题（原题的硬币总数为 3^2k，天平使用次数为 3k + 1，这里只讨论了 k = 1 时的情形）。