下面这个趣题出自 Using your Head is Permitted 谜题站 2016 年 8 月的题目，稍有改动。

屋子里有若干个人，任意两个人都有恰好 1 个共同的朋友。这有可能吗？有可能。比方说，屋子里有 9 个人，其中 8 个人正好组成 4 对朋友，第 9 个人则和前面 8 个人都是朋友。容易验证，任意两个人都有恰好 1 个共同的朋友。我们可以用下面这个图表示此时这 9 个人之间的朋友关系，其中每个点代表一个人，如果两个人是朋友，就在他们之间连一条线。

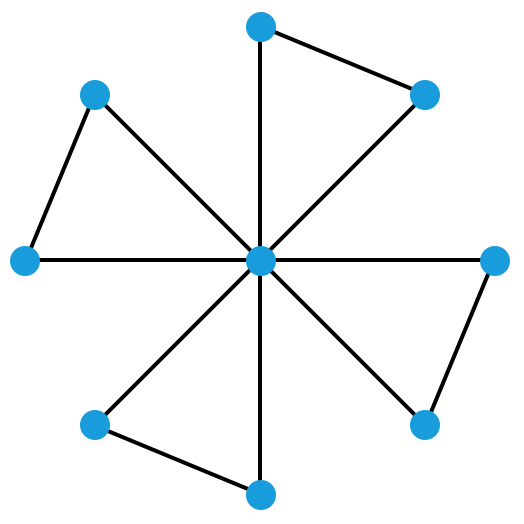
除了上图展示的情况之外，我们还能构造出很多别的同样满足要求的情况。事实上，上述方案可以扩展到一切奇数个人的情况，比如下面这样：

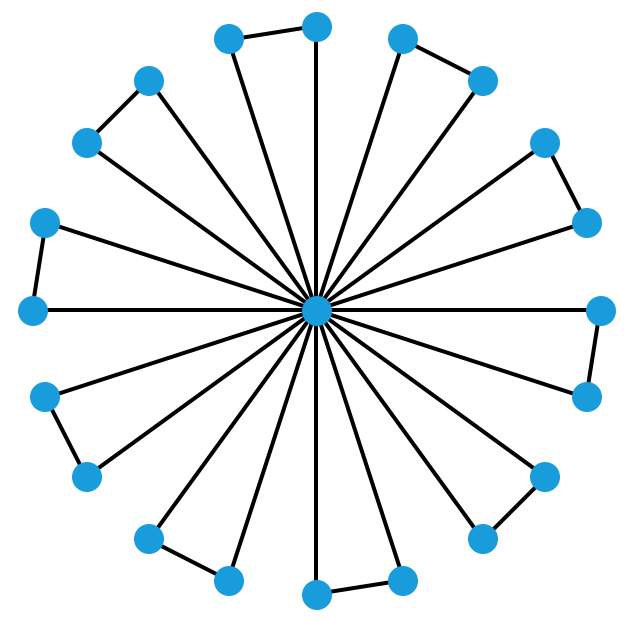
现在，假设屋子里有若干个人，任意两个人都有恰好 2 个共同的朋友。这有可能吗？有可能。比方说，屋子里有 4 个人，他们互相之间都是朋友。容易验证，任意两个人都有恰好 2 个共同的朋友。我们可以用下面这个图表示此时这 4 个人之间的朋友关系。

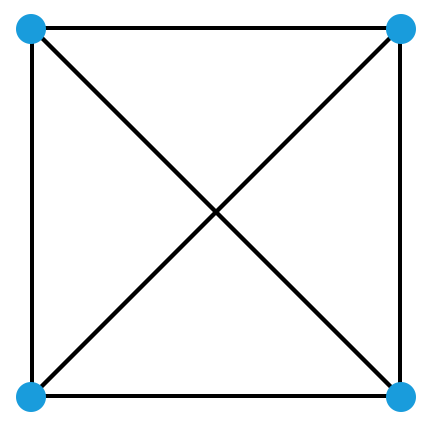
我们的问题是，除了上图展示的情况之外，还有别的同样满足要求的情况吗？

 

 

 

 

 

 

 

 

有。想象屋子里有 16 个人，他们站成了一个 4 × 4 的方阵。每行里的 4 个人互相之间都是朋友，每列里的 4 个人互相之间也都是朋友。于是，对于任意两个同一行或者同一列的人来说，都恰好有 2 个共同的朋友，即这一行或者这一列的另外两个人；对于任意两个既不同行又不同列的人来说，也都恰好有 2 个共同的朋友，即与我同行与你同列的人，以及与你同行与我同列的人。我们可以用下面的这个图表示此时这 16 个人之间的朋友关系（我们把同一行的点以及同一列的点都稍微错开了一些，使得连线不会重叠在一起）。

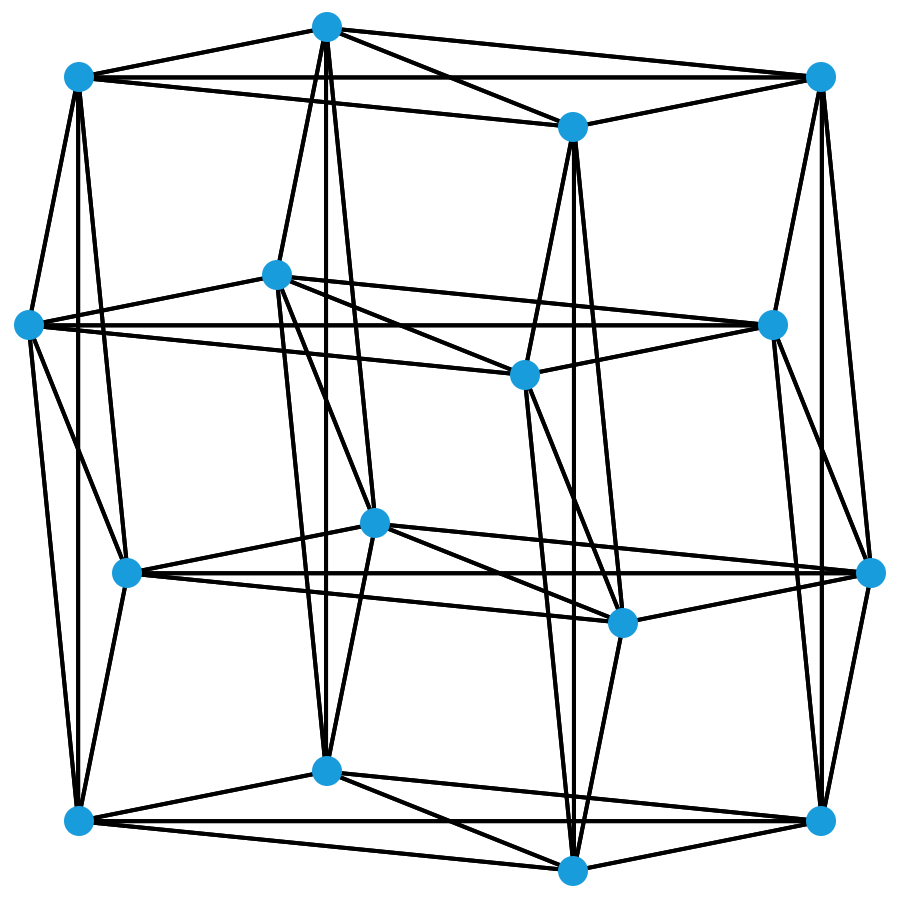
那么，除此之外，还有没有别的满足要求的解呢？有，比如下面这个图：

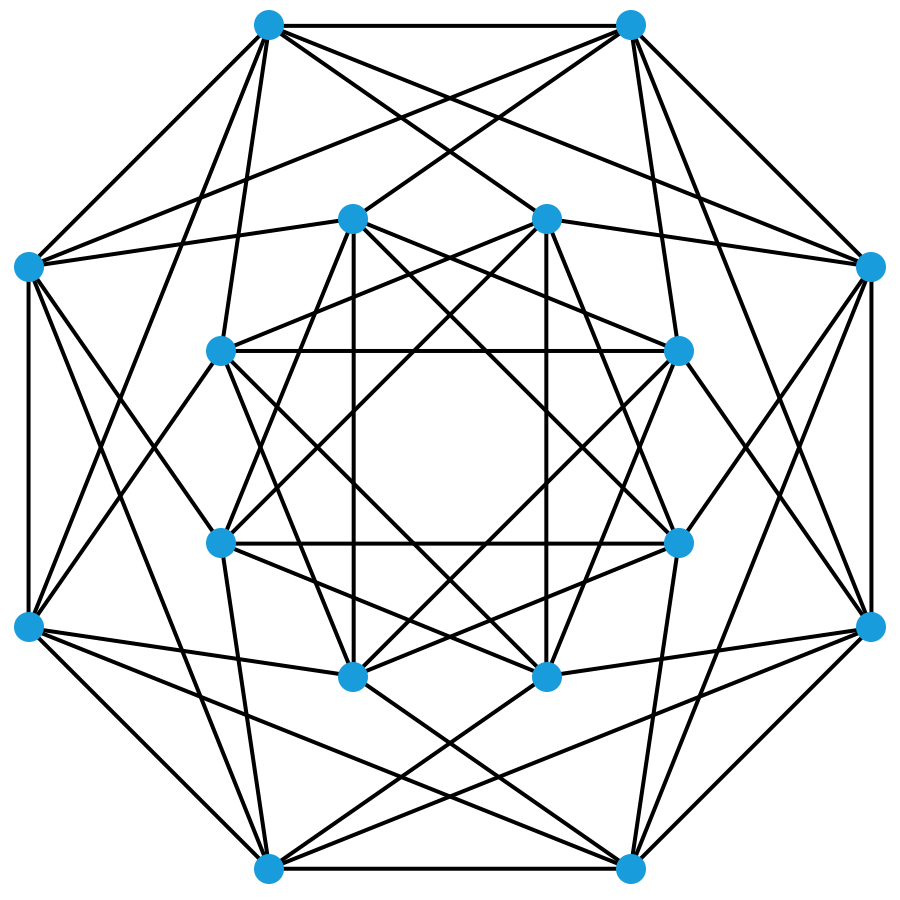
上面这两个图有很多类似的地方：它们都有 16 个点， 48 条连线，每个点都恰好引出了 6 条连线。不过，这两个图确实是本质不同的两个图。你可以这样看出来：前面这个图中，与每个点相邻的 6 个点互相之间连成的是两个三角形；而后面这个图中，与每个点相邻的 6 个点互相之间连成的是一个“圈”。

任意两个人都有恰好 2 个共同的朋友，究竟有多少种可能的情况呢？现在，我们已经看到了三个解。第一个解是 4 个互相之间都有连线的点。在图论中，我们通常用 K₄ 来表示这个图。第二个解则是借助一个 4 × 4 的方阵构造出来的。在图论中，这个图叫做 4 × 4 rook’s graph ，因为它相当于国际象棋中的车（rook）摆成 4 × 4 的方阵后互相之间能否攻击的示意图。

真正神奇的就是问题的第三个解了。它叫做 Shrikhande graph 。这是由印度数学家 Sharadchandra Shankar Shrikhande 在 1959 年发现的。在图论中， Shrikhande graph 是一个非常神奇的图。

如果一个图的每个点都引出了相同数目的线，我们就说这个图是一个“正则图”（regular graph）。如果一个正则图有 v 个点，每个点都引出了 k 条线，并且它额外地满足，任意两个相邻的点之间都恰好有 λ 个公共邻点，任意两个不相邻的点之间都恰好有 μ 个公共邻点，我们就说这个图是一个“强正则图”（strongly regular graph），用符号 srg(v, k, λ, μ) 表示。

显然， n × n rook’s graph 属于强正则图 srg(n², 2n – 2, n – 2, 2) 。那么反过来，满足 srg(n², 2n – 2, n – 2, 2) 的图是否一定就是 n × n rook’s graph 呢？基本上是，除了唯一的一个反例：当 n = 4 时， Shrikhande graph 也满足 srg(n², 2n – 2, n – 2, 2) 。

这篇文章的题目也反映出了 Shrikhande graph 的独特之处。如果任意两个点都有恰好 2 个公共邻点，那么除了 K₄ 和 n × n rook’s graph 以外， Shrikhande graph 是唯一满足要求的解了。也就是说，任意两个人都有恰好 2 个共同的朋友，可能的情况一共就只有 3 种。