假设平面上有 1 + 2 + 3 + … + n 个小球，每个小球的质量都是 1kg 。它们排成了一个三角形阵，具体地说，它们排成了一个倒置的、以 (0, 1) 为顶点的等边三角形。这个三角形阵作为一整个物体，它的重心的 y 坐标是多少？我们有两种不同的求解方法。
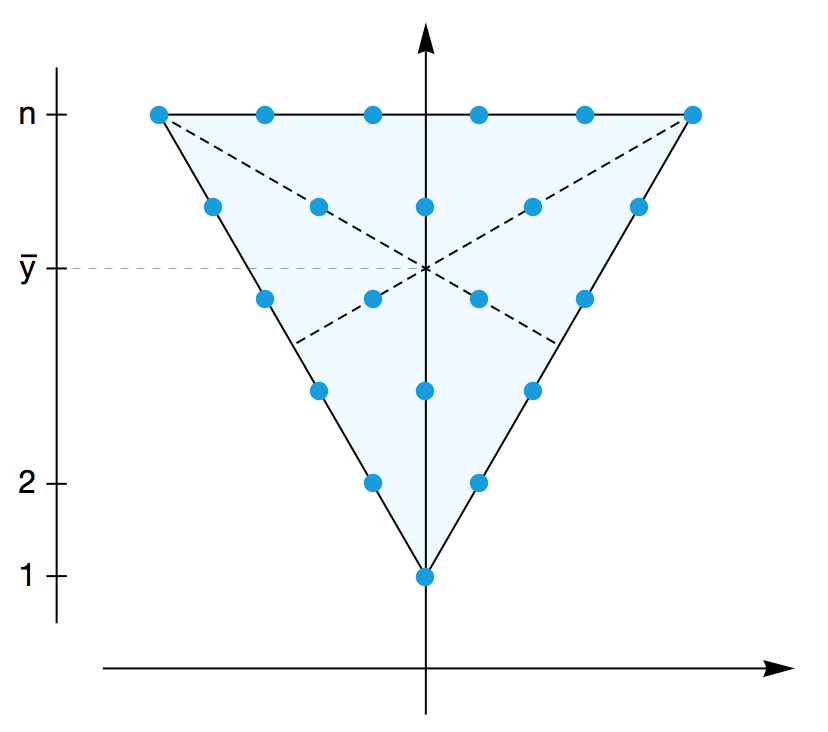
第一种方法是暴力方法。这个物体的重心的 y 坐标，一定等于所有小球的 y 坐标的平均值，即
(1 × 1 + 2 × 2 + 3 × 3 + … + n × n) / (1 + 2 + 3 + … + n)
或者写作
(12 + 22 + 32 + … + n2) / (n · (n + 1) / 2)
另一种方法则是利用图形的对称性。由对称性，整个三角形阵的重心显然应该位于这个三角形各边中线的交点上，一些经典的几何结论可以告诉我们，这个交点正好把每条中线都分成了 1 : 2 两段。因而，这个点的 y 坐标就是
1 + 2 · (n – 1) / 3 = (2 n + 1) / 3
这两种方法求出来的答案应该相等。于是，我们得到了等式
(12 + 22 + 32 + … + n2) / (n · (n + 1) / 2) = (2 n + 1) / 3
即
12 + 22 + 32 + … + n2 = n · (n + 1) · (2 n + 1) / 6
这个方法是我在 Proofs Without Words II – More Exercises in Visual Thinking 一书里看到的。
有点意思
貌似不太好推广啊，比如立方和。
唔，我试试正四面体之类的会给出什么东西……
对了，昨天晚上我试了下，一开始用的四棱锥……因为直接就是立方和了。但是对称性不好。
最后结果有点出入，只在n→∞才一致，大概是因为虽然点阵的分布是均匀的，但跟四棱锥真正的均匀分布还是不一样的。
然后试了下正四面体，有点麻烦，要消去一坨东西，不过最后还是得出来了立方和的。不知有没有更简单的几何方法。
竟然不是lochost8080回复“已阅”！
少打了几个字母。。。localhost8080
可以用杨辉三角的性质和高次相减的方法
二维表述的证明：
设点阵(x1，y1 ), (x2，y2 ), …, (xn，yn )为多边形各顶点;
则其质心坐标为O(∑x n/n, ∑y n/n);
以O为圆心的圆为(x-∑x n/n)2+(y-∑y n/n)2=C （C为常数，任意半径的平方。）;
对于其上一点P，有(xp-∑x n/n)2+(yp-∑y n/n)2=C ;
展开其，两边乘以n，
nxp2-2xp∑x n +n (∑x n/n)2 +nyp2-2yp∑y n +n (∑y n/n)2 =nC ;
调整常数，
∑(xp2-2xpx n+x n2+ yp2-2ypy n+y n2)=nC-[n (∑x n/n)2 +n (∑y n/n)2-x 12-y12-x22-y22-…-x n2-y n2]=C’ （易知C’亦为常数）;
从而，
∑[(xp- x n) 2+(yp- yn) 2]= C’ .
命题得证。
推广至多维形式：
由定理二维形式的证明可以看出，升维后所多出的变量（例如z）及各展开项系数是决定升维后定理成立的关键。
由于对于任意维度D，设该维度下的各广义球方程都可表述为：
∑d[x(d)-a(d)]2=r2
其中，x(d)为d维空间的各轴或曰参数，a(d)为球心在各轴上投影坐标，r为半径；
设其圆心为O[∑x(1) n/n, ∑x(2) n/n,…,∑x(d) n/n]，
即点集x(1) n, x(2) n,…,x(d) n的广义质心，则对其上一点P，有
∑d[x(d)p-∑nx(d) n/n]2=r2
两边乘以n，则其展开式中，x(d)p∑x(d) n其系数恒为-2，说明总可以将其写为：
∑d{∑n[x(d)p- x n ]2}= C(常数)
的形式。
大神这个月怎么更的那么早
迷之高产
对对称性的分析有一个问题: 1:2 的比例是在密度均匀的情况下推导的，如果质量集中到有限个点上，这个结论应该如何证明呢？我在这里理解的不太好，请大家指导一下，谢谢。
质量均匀分布在三个顶点的话也容易推导对称性，所以你可以先看最里面三个点组成的三角形，重心是在中心的，然后逐渐扩大
似乎博主在避免使用LaTeX？
记得我高二的时候遇到了这个题目，就是用对称法证明的。
大神，请问下有没有学习mathematica的好教程推荐下，网上找了下，貌似都太老了
很妙啊，长了见识
这个推导不新颖了，我在高中的时候，就接触过，我的高中数学老师自己写的一份资料里看到过。
个人感觉求重心是个幌子吧，我给出一个更加纯粹的证明，如下：
考虑正三角形：
1
2 2
3 3 3
把这个三角形旋转120度，再旋转120度，分别得到两个三角形，如下：
3
3 2
3 2 1
还有另外一个三角形：
3
2 3
1 2 3
把这三个三角形相加，得到：
7
7 7
7 7 7
得到都是7不是偶然的，当将3替换成n时，每个元素都是2*n+1.
而每个三角形的和都是1^2+2^2+….+n^2，
所以一个三角形的和等于三个三角形相加的和再除以3.
三个三角形相加的三角形的和为 (2*n+1) * (1+n)*n/2
一个三角形的和为 (2*n+1)*(n+1)*n/2/3
所以，1^2+2^2+…n^2 = (2*n+1)*(n+1)*n/6
怎么样，这个证明优雅吧？
三维能推广吗？
抱歉！ 回复了一个不相关的帖子，但我找不到你的联系邮箱，只好在这提问了。
最近在看你的浴缸里的惊叹，对几个问题有些疑惑，特来请教。
组合问题18题，书上说本质不同的操作序列只有2的61次方种。即执行过偶数次或奇数次。但我总觉的没有这么简单。比如如下的一个4*4的小正方形：
1 0 1 0
0 1 0 1
1 1 0 0
0 0 1 1
先对其左上角的3*3小格子进行翻转，变成如下的布局：
0 1 0 0
1 0 1 1
0 0 1 0
0 0 1 1
这样就变成了一个新的4*4的小正方形了， 虽然总数还是61种，但此时的61种不同于彼时了。其实也可以说是多了一个可能的操作了，变成了61+1了
若这时再对其右下角的3*3小正方形进行翻转， 其又变成如下的布局：
0 1 0 0
1 1 0 0
0 1 0 1
0 1 0 0
又生成了一个新的可能操作， 操作数变成了61+1+1了。故我感觉远不止2的61次方种。
不知我的理解对不对？
Elegant Proof.
很棒，上面说的那个三角形证明也不错，可惜那个在立方和的时候失效，四棱锥不对称
哇，膜拜了。
学过高中数学的人都知道如何用数学归纳法证明这个公式，但是问题是这个公式是怎么来的？如何从直观上直接推出这个公式？这些疑问我一直都没有解开，但是今天看了摘自“Proofs Without Words II – More Exercises in Visual Thinking ”的一个直观证明后，终于豁然开朗了。十分感谢Matrix67的抄写。
FYI 记得高中时数学老师整理数列求和方法的时候，用阶差法推导了这个公式，利用低阶推高阶通用思路。
君子善假于物，更善假于势。做大势所趋的事，别做趋势在下行的事。就是流行的“风口论”吧。