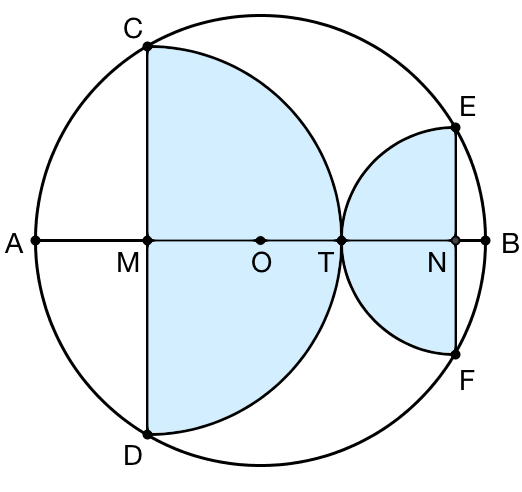
下面这个结论是 Andrew Jobbings 在 2011 年指出的：
AB 是圆 O 的一条直径， CD 、 EF 是两条垂直于 AB 的弦，并且以 CD 为直径的半圆和以 EF 为直径的半圆正好切于点 T 。那么，两个半圆的面积之和一定等于圆 O 的面积的一半。
你能证明这个结论吗？
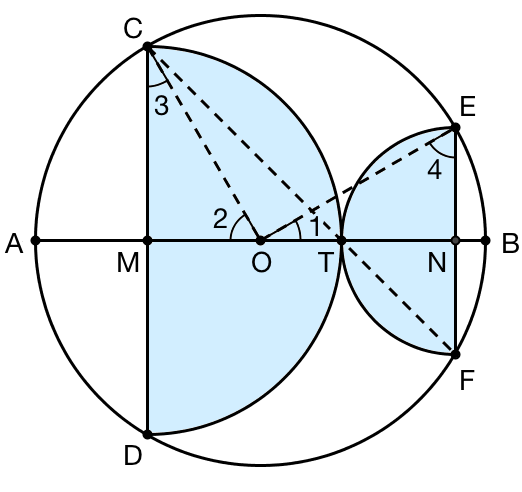
下面是 cut-the-knot 网站上给出的一种证明方法。如果把两个半圆的半径分别记作 r1 和 r2 ，把整个大圆的半径记作 R ，那么我们只需要证明
π r12 / 2 + π r22 / 2 = π R2 / 2
即
r12 + r22 = R2
由于 △MCO 是直角三角形，由勾股定理可知
MO2 + MC2 = OC2
其中 MC 就是其中左边那个半圆的半径， OC 就是整个圆 O 的半径，因而我们只需要证明 MO 就是右边那个半圆的半径即可。现在，连接 CT 、 FT ，你会发现 △MCT 和 △NFT 都是等腰直角三角形，并且 C 、 T 、 F 在一条直线上。由于圆心角的度数是圆周角的两倍，因此 ∠COE = 2 ∠CFE = 90° ，由此可知 ∠1 + ∠2 = 90° 。而 ∠2 + ∠3 = 90° ，于是 ∠1 = ∠3 。根据同样的道理，我们还可以得到 ∠2 = ∠4 。再加上整个大圆的半径 OC = OE ，就足以判定 △MCO 和 △NOE 全等了。这说明 MO = NE ，而后者正是右边那个半圆的半径。
第一次拿到沙发
相当于求等腰梯形的外接圆直径
主要是证明∠COE=90°，因此CE²=2R²。∠CTE也是直角，所以CE² =CT²+ET²=2(r₁²+r₂²)。这题难度一般？
学习来了. 好久没来逛了.
这个真是太简单了
之前的高大上数学理论怎么降格为初中数学了呢？
that’s so easy. it took me less than 30 seconds to prove it.
CMO OBE 全等，嗯 考试就用这个
初一初二程度的水题..
当然我是说玩竞赛的..
这是我第一个看完的题目，之前的我根本都看不完！！！太难
连接[C,E]; [T,C]; [T,E]; 然后盯着图看就证完了…
就是两45RT里边，两斜和[C,E]组成新的RT； 由此[C,E]=sqrt(2)*sqrt(a^2+b^2)；
又在三角形(OCE)里面，目测得[C,E]=sqrt(2)*r；
由此r^2=a^2+b^2;
证明(COE)是RT，看CE对的两圆心角即可
目测得[C,E]=sqrt(2)*r；
谁告诉你角COE是直角的？虽然确实是直角，但是需要证明啊
我表示，刚看到回复补充的那句话。。。。
关键是CTF在同一直线上，这个是怎么说明的？
对顶角相等 都为 45度
任意一个圆 某段圆弧的圆心角度数 等于 相应圆周角度数的2倍
呃为什么现在都是放些初中的家庭作业题…
真的是太妙了，唉，我还要继续进步啊，希望以后多出这些简单的，让更多的小学生认识你
是不是可以这么想：当两个半圆中的任意一个无限趋近于0，另一个半圆的直径将会无限的趋近于大圆直径，当其中一个半圆的面积为0时，另一个半圆的直径就是大圆的直径，所以两个小圆的半径之和等于大圆的一半。文科数学没学过这种极限的东西，不知道能不能这样证明。求大神指点。
圆心角和圆周角的概念早都还给老师了，更别说知道圆心角度数是圆周角的二倍了。不过还是证明出来了。
设圆M半径是R1,圆N的半径是R2,且OT为x，
然后三角形CMO和三角形ONE都为直角三角形，且CO=OE，那么R1的平方+(R1-x)的平方=CO的平方=OE的平方=R2的平方+(R2+x)的平方。根据此式可推导出x=R1-R2，所以其实OM=R2，在三角形CMO中可以得到R1平方+R2平方=R平方
wow牛B
虽然辅助线一出来就能看出来，但不得不感叹相当的精巧啊~
我想出来证∠COE=∠CNE=90°的方法,没有楼主的简洁,
最后证△MCO 和 △NOE全等基本一样, 当然证全等还可以只用一组锐角相等因为斜边相等都是圆半径
连接
OC, OE, OD, OF, CF, DE
CNF, DNE 两组三点共线且CF=DE, CF⊥DE
△COF≌△DOE
∠OEN=∠OCN
CEON四点共圆
∠COE=∠CNE=90°
在没想出几何方法前想到一种暴力的三角方法法证明∠COE = π/2
首先M,N必须分居圆心O的一两侧, 这直观上是显然的, 证明也不难:
比如假设M在O的右侧并且向右侧画半径为r1的半圆, 那么
OM = √(r^2 – r1^2) = √[(r + r1)(r – r1)] > √(r – r1)^2 = r – r1, 即
OM + r1 > r T会到AB延长线上与题意不符
所以可设∠EOB = α, ∠COB = β, 并且一定有 0 < α < π/2, π/2 < β < π
r1 = r sin α, r2 = r sin β
由两圆相切的性质MN = r1 + r2, 但另一方面 MN = r cos α – r cos β (注意是减号因为cos β < 0)
所以有 sin α + sin β = cos α – cos β
等式两边分别用和差化积公式:
2sin[(α + β) / 2]cos[(α – β) / 2] = 2sin[(α + β) / 2]sin[(β – α ) / 2]
由于有 π/2 < α + β < 3π/2
π/4 < (α + β) / 2 < 3π/4
sin[(α + β) / 2] ≠ 0
cos[(α – β) / 2] = sin[(β – α ) / 2]
sin[(β – α ) / 2] – cos[(β – α) / 2] = 0
√2 sin[(β – α ) / 2 – π/4] = 0
由于 0 < (β – α) / 2 < π / 2
(β – α) / 2 = π/4
∠COE = β – α = π/2 得证
这里后面当然可以用全等但是也可以用三角暴力到底:
由于有, β – α = π/2
sin β = sin (α + π/2) = cos α
两半圆面积的和 = π/2 (r1^2 + r2^2) = πr^2/2(sin^2 α + sin^2 β) = πr^2/2(sin^2 α + cos^2 α)
= πr^2/2
Yes! Finally someone writes about website.
Ahaa, its pleasant conversation concerning this paragraph at this place at this web site, I have read all that, so at this time me also commenting at this place.
“We have discovered a tremendous amont about how to decrease the cost of flexibility,” she mentioned.
My web blog :: 여성알바
Only persons aged 18 years or over and resident iin Excellent Britaain (England, Scotland
or Wales) are eligible to enter the CHSW Lottery and CHSW Raffle.
my webpage … site
OMG! This is amazing. Ireally appreciate it~ May I show my
inside to a secret only I KNOW and if you
want to really findout? You really have to believe mme and have faith and
I will show how to change your life Once again I
want to show my appreciation and may all the blessing goes to you now!.
I believe people who wrote this needs true loving because it’s a blessing.
So let me give back and show back my secrets on change your life and if you want to with no joke truthfully see I
will share info about how to get connected to girls for free Don’t forget..
I am always here for yall. Bless yall!
I do agree with all of the concepts you have offered
to your post. They’re very convincing and will certainly work.
Still, the posts are very short for newbies.
May just you please lengthen them a bit
from next time? Thank you for the post.
But perhaps the day’s noise tends to make the quiet of
drawing much more numinous and clarifying.
Stop byy my blog :: 노래방알바
They are all locations where folks are most likely to be playing games.
Feel freee to visit my site … site
The on the internet scratch caqrd gwmes offer you payouts
as hogh as $500,000 and can be had for as small as $.05.
Feel free to surf to my webpage 메가밀리언
All of the finest on the net casinos in the globe
have excellent bonuses that you can claim.
Also visiit my blogg post: 카지노사이트
Moreover, the platform delikvers yoou with detailed economic
guidance.
Here iis my blog ppost :: 무방문 대출
Posssessing a steady revenue is a important indicator oof your
ability to repay the borrowed amount.
My web page … 정부지원대출
There is no better wayy to get your account funded and ready to go.
Also visit myy web site 토토사이트검증
Kangwon Land Casino is inside Kangwon Land, a complex resort
facility located inn the highland in Baegunsan Mountain (situated in Sabuk-ri, Sabuk-eup, Jeongseon-gun, Gangwon-do) at 883 m above sea level.
Here iis my site … here
These range from classic 3-reel games to massive progressive jackpots, with denominations starting from
$.01 per payline.
Visit my homepage 바카라사이트
Nevertheless, the databases that shop the token alongside the corresponding data are high-danger targets.
Feel free tto visit my site 파워볼중계
I’m truly enjoying the design and layout of your blog.
It’s a very easy on the eyes which makes it much more enjoyable for me
to come here and visit more often. Did you hire out a
designer to create your theme? Superb work!
Saved as a favorite, I love your site!
hey there and thank you for your info – I have certainly
picked up anything new from right here. I did however expertise a few
technical points using this site, since I experienced to reload the web site
many times previous to I could get it to load correctly. I
had been wondering if your web host is OK? Not that I am
complaining, but sluggish loading instances
times will very frequently affect your placement in google and can damage
your high quality score if ads and marketing with Adwords.
Anyway I’m adding this RSS to my e-mail and could look out for a
lot more of your respective fascinating content. Ensure that you update this
again soon.
We are a gaggle of volunteers and starting a new scheme in our community.
Your website offered us with useful info to work on. You’ve
done an impressive process and our whole group will likely be grateful to you.
Good post! We are linking to this great article on our website.
Keep up the great writing.
It’s awesome for me to have a web site, which is good in favor of my know-how.
thanks admin
It’s really a cool and helpful piece of info. I am glad that you just shared this
useful info with us. Please keep us up to date like this.
Thank you for sharing.
Hello there, I found your website by way of Google even as
looking for a related topic, your website came up, it looks good.
I have bookmarked it in my google bookmarks.
Hi there, just changed into aware of your blog thru Google, and located that it is really informative.
I am gonna watch out for brussels. I will be grateful if you happen to proceed this in future.
Lots of folks can be benefited out of your writing.
Cheers!
You really make it appear so easy together with your presentation but I find this matter to be actually one
thing that I feel I would by no means understand.
It seems too complex and extremely vast for me. I’m having a
look ahead for your next put up, I’ll attempt to get the hold
of it!
Marvelous, what a blog it is! This website presents helpful facts to us, keep it up.
For the reason that the admin of this site is working, no hesitation very soon it will
be well-known, due to its quality contents.
I’ve been exploring for a bit for any high-quality articles or blog posts in this kind of space .
Exploring in Yahoo I finally stumbled upon this site.
Reading this info So i am glad to show that I have a very
good uncanny feeling I discovered exactly what
I needed. I most indubitably will make certain to
do not omit this site and provides it a look on a constant basis.
Why people still use to read news papers when in this technological world all
is available on net?
Wonderful blog! I found it while browsing on Yahoo News.
Do you have any tips on how to get listed in Yahoo News?
I’ve been trying for a while but I never seem to get there!
Appreciate it
You actually make it seem so easy with your presentation but I find
this topic to be really something that I think I would never understand.
It seems too complicated and extremely broad for me.
I’m looking forward for your next post, I’ll try to get the hang
of it!
That is really fascinating, You are an overly professional blogger.
I have joined your rss feed and look ahead to in quest of extra of your wonderful post.
Also, I’ve shared your site in my social networks
It’s actually a nice and helpful piece of information. I’m happy that
you shared this helpful info with us. Please
stay us informed like this. Thanks for sharing.
Hi there to every one, as I am in fact keen of reading this website’s post to be
updated daily. It contains fastidious data.
Hello there, I discovered your site via Google while looking for a related topic, your web site got here
up, it seems to be great. I’ve bookmarked it
in my google bookmarks.
Hi there, simply was alert to your weblog through
Google, and found that it’s truly informative.
I’m gonna be careful for brussels. I’ll appreciate should you proceed this in future.
Lots of other people will probably be benefited out
of your writing. Cheers!