字符串 hello 当中连续出现了两个 l 。字符串 prototype 当中连续出现了两个 ot 。字符串 nonsense 当中连续出现了两个 nse 。如果某个字符串中连续出现了两个相同的片段，换句话说这个字符串里面含有形如 XX 的模式（其中 X 代表一个子串），我们就说这个字符串中含有一个“平方”（square）。如果某个字符串中没有平方出现，我们就说这个字符串是“免平方”的（square-free）。

如果只使用两种字符，比方说字符 0 和字符 1 的话，我们只能构造出一些长度非常有限的免平方字符串。事实上，我们只能构造出以下 6 个免平方字符串： 0 、 1 、 01 、 10 、 010 、 101 。然而，如果允许使用三种字符，比方说字符 0 、 1 、 2 的话，我们不但能够构造出任意长的免平方字符串，还能构造出无限长的免平方字符串。在继续阅读下去之前，你不妨先自己试试看。

 

让我们先来看一个与刚才的讨论似乎毫不相关的问题。你能找出下面这个序列的规律吗？（考虑到字符串本质上就是一个字符序列，因此下面我们会经常混用“字符串”和“序列”这两个概念。）

0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1 …

答案：它们分别表示 0, 1, 2, 3, 4, … 的二进制表达中有多少个数字 1 ，其中 0 代表有偶数个数字 1 ， 1 代表有奇数个数字 1 。如果我还没说清楚的话，看看下表你应该就明白了。

十进制数	0	1	2	3	4	5	6	7	8	9	10	11	…
二进制数	0	1	10	11	100	101	110	111	1000	1001	1010	1011	…
1 的个数	偶数	奇数	奇数	偶数	奇数	偶数	偶数	奇数	奇数	偶数	偶数	奇数	…
序列	0	1	1	0	1	0	0	1	1	0	0	1	…

我们不妨把这个序列用 t 表示。序列 t 还有很多等价的定义，比方说，我们可以递归地定义，当 n 为偶数时， t(n) = t(n/2) ，当 n 为奇数时，t(n) = 1 – t(n-1) ；最后再规定 a(0) = 0 ，整个序列就唯一地确定了。你会发现，定义方式虽然是新的，但是背后的实质仍然没变。如果 n 是偶数，那么 n 的二进制表达的最后一位就是数字 0 ，除以 2 其实就相当于是去掉这个数字 0 ，数字 1 的个数的奇偶性显然没变。如果 n 是奇数，那么 n 的二进制表达的最后一位就是数字 1，而 n – 1 的二进制表达的最后一位则是数字 0 ，这两个二进制数仅在最后一位有所不同，因此数字 1 的个数的奇偶性肯定是相反的。因而，不断这样递推下去，最后得到的序列与刚才的序列 t 一模一样。由于对于所有的偶数 n ， t(n) = t(n/2) 始终成立，因此这个序列还有一个非常炫的性质：把序列中的 t(1), t(3), t(5), … 都去掉，仅保留 t(0), t(2), t(4), … ，由此得到了一个新的无穷序列，它和原来的序列完全相同！另外，由于对于所有的奇数 n ， t(n) = 1 – t(n-1) = 1 – t((n-1)/2) 始终成立，你也可以选择去掉 t(0), t(2), t(4), … ，保留 t(1), t(3), t(5), … ，由此得到一个新的无穷序列，它和原序列的每一项都正好相反。

在介绍序列 t 时，很多地方会采用另一种等价的定义方式：从 0 出发，不断执行“取反并后置”的操作，最终得到的序列就是序列 t 。所谓“取反”，就是把所有的 0 全部变成 1 ，把所有的 1 全部变成 0 ；所谓“后置”，就是把所得的字符串接在当前字符串的后面。从 0 出发，取反后得 1 ，把它加在 0 后面便得到 01 ； 01 取反后得 10 ，把它加在 01 后面便得到 0110 ； 0110 取反后得到 1001 ，把它加在 0110 后面便得到 01101001 ……不断这样下去，我们就会得到序列 t 。

0 → 01 → 0110 → 01101001 → 0110100110010110 → …

为什么？因为这种序列生成法的本质仍然是在统计二进制数的数字 1 的个数。我们不断地根据二进制数的规律，利用 t(0) 到 t(2ⁿ – 1) 的值，推出 t(2ⁿ) 到 t(2ⁿ⁺¹ – 1) 的值。比方说，序列 t 的前 4 个数分别代表 00, 01, 10, 11 这 4 个二进制数中数字 1 的个数的奇偶性，那么序列 t 接下来的 4 个数就应该分别代表 100, 101, 110, 111 这 4 个二进制数中数字 1 的个数的奇偶性。前 4 个二进制数与后 4 个二进制数的区别仅仅在于最前面的那个数字 1 ，因而它们所含的数字 1 的个数的奇偶性应该正好相反。因此，如果序列 t 的前 4 个数分别是 0, 1, 1, 0 ，那么序列 t 接下来的 4 个数就应该完全反过来，分别是 1, 0, 0, 1 了。

 

从 1906 年到 1914 年，挪威数学家 Axel Thue 发表了一系列论文，第一次对这个序列进行了细致的研究，成为了 combinatorics on words 这个新的数学分支的开山之作。 1921 年，美国数学家 Marston Morse 把 Thue 提出的序列用在了微分拓扑上，因而这个序列最终被命名为了 Thue-Morse 序列。

Thue-Morse 序列有很多非常漂亮的性质。如果某个字符串中连续出现了两个相同的片段，但它们有一个字符的交叉，换句话说这个字符串当中出现了形如 aXaXa 的模式，其中 X 代表一个子串， a 代表一个字符，那么我们就说 aXa 在这个字符串当中发生了“重叠”（overlap）。例如，单词 banana 当中的 ana 就出现了重叠，单词 Mississippi 中的 issi 也出现了重叠。如果某个字符串中没有重叠出现，我们就说这个字符串是“免重叠”的（overlap-free）。下面我们就来证明 Thue-Morse 序列的一个最为重要的性质：它是免重叠的。

我们采用反证法。假如 Thue-Morse 序列存在重叠子串，那么在所有的重叠子串中一定有一个最短的重叠子串。这意味着， Thue-Morse 序列将会包含 aXaXa 的模式，其中 X 表示某个子串， a 表示某个字符，并且 X 的长度已经达到最小。首先我们证明， X 的长度不可能是奇数。否则，三个 a 的位置编号的奇偶性相同，因而如果我们从第一个 a 开始，间隔地读出各个字符，就会得到形如 aX’aX’a 的结果，其中 X’ 就是从 X 当中抽出的字符串，长度是 X 的一半（取下整）。然而，前面我们已经提到过 Thue-Morse 序列的性质了：间隔地抽取字符，得到的新字符串要么就是 Thue-Morse 序列，要么取反后就是 Thue-Morse 序列。这说明， aX’aX’a ，或者它取反后的结果，其实就是 Thue-Morse 序列的子串。因而， Thue-Morse 序列当中存在比 aXaXa 更短的重叠现象，这与 X 的长度的最小性矛盾。

接下来我们证明， X 的长度也不可能是偶数。首先注意到， 4n, 4n + 1, 4n + 2, 4n + 3 的二进制表达中，只有最后两位数字不一样，它们依次是 00, 01, 10, 11 。因此， t(4n), t(4n + 1), t(4n + 2), t(4n + 3) 的值要么依次是 0, 1, 1, 0 ，要么依次是 1, 0, 0, 1 。所以，如果我们把 Thue-Morse 序列四个数四个数地看作一组，你会发现 Thue-Morse 序列就是由一个一个的 (0, 1, 1, 0) 和 (1, 0, 0, 1) 组成的。

如果 X 的长度是大于等于 4 的偶数，那么不管 aXaXa 在 Thue-Morse 序列中的什么地方出现，前一个 aXa 里必然会包含某个四元组的中间两项，不妨假设这是 aXa 中的第 i 项和第 i + 1 项。另外，别忘了 X 的长度是一个偶数，因此前一个 aXa 需要向右移动奇数个单位才能和后一个 aXa 重合。这就矛盾了：向右移动奇数个单位后， aXa 的第 i 项和第 i + 1 项将会对应于另一个四元组的前面两项或者后面两项，于是前一个 aXa 的第 i 项和第 i + 1 项是两个相同的数字，后一个 aXa 中的第 i 项和第 i + 1 项是两个不同的数字，这显然是荒谬的。

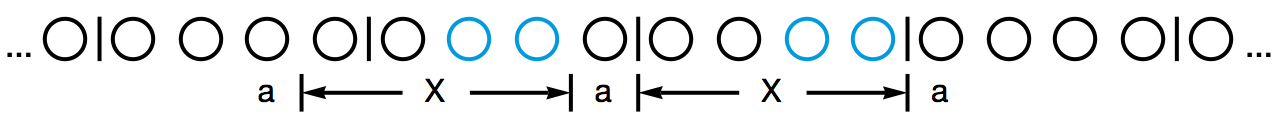
如果 X 的长度等于 2 ， aXa 的长度会非常短，以至于会发生这样的情况：没有任何一个四元组的中间两项落在了前一个 aXa 的范围里，此时前面的推理就失效了。不过没关系，如果真的发生了这种情况， aXaXa 的位置只可能像下图这样，此时前一个 aXa 的第 1 项和第 2 项对应于某个四元组的后两项，但后一个 aXa 的第 1 项和第 2 项就会对应于下一个四元组的中间两项，矛盾依然存在。

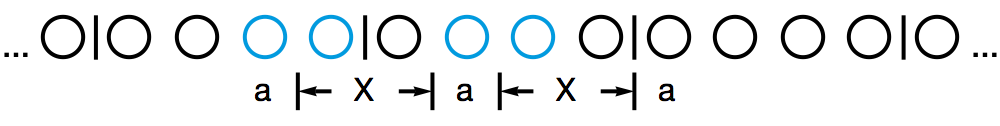
最后，如果 X 的长度为 0 呢？这就更不可能了。在 Thue-Morse 序列中，任意三个连续的字符都会涵盖到某个四元组的前面两项或者后面两项，因而包含两个不同的数字。因此，在 Thue-Morse 序列中绝不可能有形如 aaa 的子串出现。

综上所述， Thue-Morse 序列中不可能包含形如 aXaXa 的子串，即 Thue-Morse 序列是免重叠的。

 

有了这个结论之后，我们就能解决本文最初提到的问题了。借助 Thue-Morse 序列，我们可以得到一个无限长的免平方字符串，其中只含 0 、 1 、 2 三种字符。方法很简单：只需要依次列出 Thue-Morse 序列中相邻两个 0 之间有多少个 1 即可。在 Thue-Morse 序列中，第 1 个数字 0 和第 2 个数字 0 之间夹着 2 个数字 1 ，第 2 个数字 0 和第 3 个数字 0 之间夹着 1 个数字 1 ，第 3 个数字 0 和第 4 个数字 0 之间夹着 0 个数字 1 ，第 4 个数字 0 和第 5 个数字 0 之间夹着 2 个数字 1 ……于是，我们就得到了一个以 2, 1, 0, 2 开头的无限字符串。注意，由于 Thue-Morse 序列中不可能出现三个或者三个以上的连续数字 1 ，因此所得字符串中不会出现大于等于 3 的数字，只有数字 0 、 1 和 2 。

Thue-Morse 序列： 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0…
新的序列：2, 1, 0, 2, 0, 1, 2, …

为什么由此得到的序列是免平方的呢？很简单。如果新的序列里面出现了某个平方，比如 a₁a₂a₃…a_na₁a₂a₃…a_n ，这就意味着 Thue-Morse 序列里出现了 0 1^a1 0 1^a2 0 1^a3 0 … 0 1^an 0 1^a1 0 1^a2 0 1^a3 0 … 0 1^an 0 （其中 1^a1 表示连续 a₁ 个数字 1 ，以此类推），于是形成了重叠子串，与 Thue-Morse 序列的免重叠性矛盾。

 

从 Thue-Morse 序列的免重叠性出发，我们还能得出很多有趣的推论。例如， Thue-Morse 序列一定是免立方的，即 Thue-Morse 序列中不存在形如 XXX 的子串。原因很简单：不妨假设 X = aX’ ，那么 XXX 实际上就是 aX’aX’aX’ ，其中 aX’aX’a 形成了重叠子串，又与 Thue-Morse 序列的免重叠性矛盾了。由此可以进一步推出， Thue-Morse 序列永远不会发生循环。原因很简单：如果 Thue-Morse 序列从某处开始发生循环，这就直接与 Thue-Morse 序列的免立方性矛盾了。

同时， Thue-Morse 序列是一个“复现序列”（recurrent sequence），意即 Thue-Morse 序列中的每一个子串都会出现无穷多次。这个事实背后的原因也很简单。比方说，我们在 Thue-Morse 序列当中取出 t(6) 到 t(10) 这么一段，它们是 0, 1, 1, 0, 0 ，表示二进制数 0110, 0111, 1000, 1001, 1010 的数字 1 的个数的奇偶性。那么， 0, 1, 1, 0, 0 今后一定会出现无数多次。在数到二进制数 110110, 110111, 111000, 111001, 111010 时，我们会再一次得到 0, 1, 1, 0, 0 ；在数到二进制数 1010110, 1010111, 1011000, 1011001, 1011010 时，我们会再一次得到 0, 1, 1, 0, 0 。这样的机会显然还有无穷多，例如，在数到二进制数 1101001000110, 1101001000111, 1101001001000, 1101001001001, 1101001001010 时，我们会再一次得到 0, 1, 1, 0, 0 。

构造一个复现序列很简单，任何一个循环序列即满足要求，比如 0, 1, 0, 1, 0, 1, … 。而 Thue-Morse 序列则告诉了我们：存在不是循环序列的复现序列。

 

最后，我们再不加证明地给出两个与 Thue-Morse 序列有关的神奇结论。对于哪些正整数 k ≥ 2 ，存在两个大小相等的整数集合 A = {a₁, a₂, a₃, …, a_n} 和 B = {b₁, b₂, b₃, …, b_n} ，使得

a₁ + a₂ + a₃ + … + a_n = b₁ + b₂ + b₃ + … + b_n
a₁² + a₂² + a₃² + … + a_n² = b₁² + b₂² + b₃² + … + b_n²
……
a₁^k + a₂^k + a₃^k + … + a_n^k = b₁^k + b₂^k + b₃^k + … + b_n^k

即集合 A 里的所有数与集合 B 里的所有数从 1 次方和到 k 次方和全都相等？当然，集合 A 和集合 B 必须是两个不同的集合。答案是，对于所有的正整数 k ≥ 2 ，满足要求的解都是存在的。利用 Thue-Morse 序列，我们可以得出一种 n = 2^k 的构造解，方法如下：取出 Thue-Morse 序列的前 2^k+1 位，即 t(0), t(1), …, t(2^k+1 – 1)，如果 t(i) = 0 ，就把 i 放进集合 A 里，如果 t(i) = 1 ，就把 i 放进集合 B 里。

i	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
t(i)	0	1	1	0	1	0	0	1	1	0	0	1	0	1	1	0

当 k = 3 时，如上表所示，根据规则，我们应该把 0, 3, 5, 6, 9, 10, 12, 15 分为一组，把 1, 2, 4, 7, 8, 11, 13, 14 分为另一组。神奇的事情出现了：下面三个等式真的是成立的！

0 + 3 + 5 + 6 + 9 + 10 + 12 + 15 = 1 + 2 + 4 + 7 + 8 + 11 + 13 + 14
0² + 3² + 5² + 6² + 9² + 10² + 12² + 15² = 1² + 2² + 4² + 7² + 8² + 11² + 13² + 14²
0³ + 3³ + 5³ + 6³ + 9³ + 10³ + 12³ + 15³ = 1³ + 2³ + 4³ + 7³ + 8³ + 11³ + 13³ + 14³

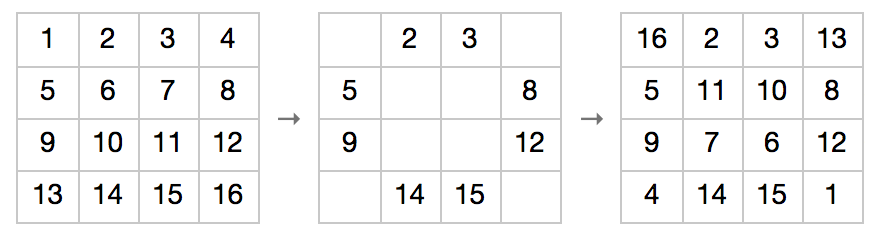
Thue-Morse 序列还能帮忙构造幻方。 1977 年， Adler Allan 和 Shuo-Yen Robert Li 给出了一种算法，可以利用 Thue-Morse 序列构造 2ⁿ × 2ⁿ 的幻方（其中 n ≥ 2 ）。首先，从左至右从上至下地把 1 到 2²ⁿ 的数填入 2ⁿ × 2ⁿ 的方格里。然后，如果 Thue-Morse 序列中的第 i 个数是 0 （即 t(i – 1) = 0 ），就把 i 从方格里拿出来。最后，把所有拿出来的数倒序放回方格，我们就得到了一个幻方。下图所示的是 n = 2 时的例子。由于 Thue-Morse 序列中的第 1, 4, 6, 7, 10, 11, 13, 16 个数是 0 ，因而我们把这些数从 4 × 4 的方阵中取出来；把它们以相反的顺序放回去后，可以验证，方阵中的每一行、每一列和两条对角线上的数字之和都是 34 。

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
t(i – 1)	0	1	1	0	1	0	0	1	1	0	0	1	0	1	1	0

 

网上闲逛时偶然看到 Thue-Morse 序列，于是陷入 Wikipedia 的相关词条不能自拔，随后又找来了这些词条后面提到的参考文献，狠狠地过了一把 combinatorics on words 的瘾。其实， Thue-Morse 序列还有很多东西值得摆谈，但是精力有限，也就只写到这里了。感兴趣的读者不妨看一看 Combinatorics on Words: Christoffel Words and Repetitions in Words 和 Automatic Sequences: Theory, Applications, Generalizations 这两本书。