今天才听说了这样一个有趣的命题：如果一个矩形可以分割为若干个小矩形，每个小矩形都有至少一边为整数长，则原矩形同样有至少一个长度为整数的边。换句话说，用至少有一边的长度是整数的小矩形拼成一个大矩形，大矩形也有至少一条整数长的边。这个命题看似简单但却很难证明，更准确地说应该是很难想到证明方法。而有趣就有趣在，这个命题的证明方法出奇的多，从图论方法到数论方法，每个证明都相当巧妙。

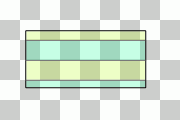
    我们所要介绍的第一个证明是我觉得最巧妙的证明方法。证明的关键在于下面这个引理：像国际象棋棋盘一样对整个平面黑白染色，那么与两坐标轴平行放置且至少一边长为偶数的矩形一定覆盖了相同面积的黑色区域和白色区域。原因很简单，看上图，该矩形中的每一个（长度为偶数个单位的）横条显然都覆盖了相同面积的黑白两色区域。

 
    
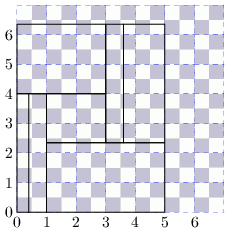
    下面，我们把整个平面分成(1/2)*(1/2)大小的正方形，并且像上面那样黑白二染色，然后把那个大矩形对齐坐标轴放在平面上，左下角和原点对齐。这个矩形内的每个小矩形都有至少一个整数边，也即至少有一边的长度是1/2的偶数倍，因此每个小矩形都覆盖了相同面积的黑色区域和白色区域。这样，整个大矩形也就覆盖了同等面积的黑白区域。

 
 
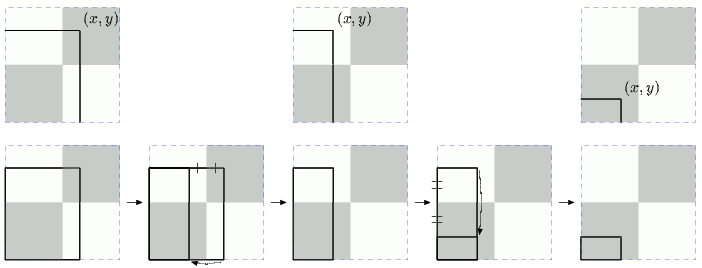
    然而，对于一个左下角与原点对齐的矩形，如果右上角(x,y)两个坐标值都不是整数的话，那么这个矩形所覆盖的黑色区域一定大于白色区域：除去黑白相等的“整”的部分，最后剩下的就是最右上角的那个未填满的1×1正方形有待讨论。坐标(x,y)的位置只有三种可能，而第一种情况可以等价地转化为第二种情况，第二种情况也可以等价地变成第三种情况，在第三种情况中我们立即看到，矩形所覆盖的黑色面积一定大于白色面积。
    如果要让整个矩形覆盖相同面积的黑色和白色，x和y至少有一个是整数才行，而这就是我们所要证明的结论了。