明天考英语,单词还没背。先冒死更新一个^_^
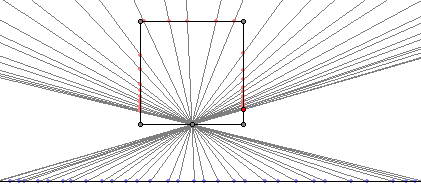
我们称一个从集合A到集合B的映射是“单射”的,如果A中的任两个相异元素都不会映射到B里的同一个元素。如果一个A→B的映射是单射的,并且B里的所有元素都被射了(满射),那么这个映射就是“双射”的。Cantor-Bernstein-Schroeder定理是说,假如存在一个从集合A到集合B的单射函数f,以及一个从集合B到集合A的单射函数g,那么A与B之间一定存在一个双射函数(即能建立起一一对应的关系,两个集合有相等的势)。这个结论并不是显然的。对于无穷集合,我们可以构造出很多这样的例子,两个映射A→B和B→A都是单射,但都不是满射的。例如,给定一个正方形和正方形外的一条直线,把正方形放到直线上滚一圈所形成的对应关系是一个从正方形上的所有点到直线上的点的一个单射函数,而连接直线上的点和正方形一边中点后与正方形的另一个交点构成了一个从直线到正方形的单射关系(如图)。那么,根据Cantor-Bernstein-Schroeder定理,我们一定可以找到一种函数,使得直线上的所有点和正方形上的所有点有一一对应的关系。
首先,让我们来证明这样一个引理:如果B是A的子集,且存在单射f: A→B,则一定存在A到B的双射函数。换句话说,假如存在一个集合到它自身的某个子集的单射函数,则这两个集合的势一定是相等的。
令集合Y为A有B没有的元素,即Y=A-B。令集合X为集合Y经过任意次函数f的迭代所能得到的所有元素,即X=Y∪f(Y)∪f(f(Y))∪f(f(f(Y)))∪… 为了方便起见,我们用f_k(t)来表示对t的元素进行k次迭代所得到的元素。一个有趣的事实是,对于任何a≠b,f_a(Y)和f_b(Y)都没有公共元素。这可以用数学归纳法来说明。为了说明f_a(Y)和f_b(Y)没有公共元素,我们只需说明f_a-1(Y)和f_b-1(Y)之间没有公共元素即可(因为f是单射的),这样又把问题归结为证明f_a-2(Y)和f_b-2(Y)的交集为空。这样一直递归下去,最终就归结为Y和f_k(Y)交集是否为空的问题,其中k为a和b的差值。但f_k(Y)显然是B的子集,而集合Y的定义是集合A中除去B后剩下的部分,它们之间显然没有公共元素。
回到上面对X的定义,注意到f(X)等于f(Y)∪f_2(Y)∪f_3(Y)∪…,于是X=Y∪f(X)。同时,我们还有A=B∪Y,于是A-X = [B∪Y] – [Y∪f(X)] = B-f(X)。这样,我们就可以把映射A→B拆成X→f(X)和A-X → B-f(X)两个部分,函数f在前者的范围内是双射的,而后一部分的象和原象是A和B的同一子集,本身就是一一对应的。于是,我们可以定义一个新的函数α(z):当元素z在集合X中时定义α(z)为f(z),否则α(z)就等于z。显然,函数α(z)是双射的。
重新回到本文最初所提到的结论:若有单射f: A→B和单射g: B→A,则一定存在A和B之间的双射。如何用上面的引理来证明这个结论呢?首先,注意到g(B)是一个A的子集。由于A→B有一个单射函数,B到g(B)有一个双射函数,那么A→g(B)也有一个单射函数。套用前面的引理,我们知道了A和g(B)间存在一个双射函数。但是g(B)和B之间也是双射的,于是我们立即得到:这两个双射函数的复合函数就是A和B之间的双射函数。
另一个有趣的证明由Julius König给出。把A和B以及两个单射函数f和g想像成一个二分图,只不过里面的边是有向的。对于A里的任何一个节点a,或者B里的任何一个节点b,我们总能够永无止境地往下走,并且(由于函数是单射的)可以倒着往回走。最后呢,要么到了某个时候倒着走走不动了,要么就走出一个圈。注意,由于函数是单射的,每一个元素都必须且只能在其中一条链(或环)上出现,于是这些链(或环)形成了一组并集为全集、交集为空的“分割”。对于任一个环上的所有顶点,函数f(或者g)显然是一个双射函数(注意由于这是二分图,环的长度必然为偶数);对于任一条链上的所有顶点,f和g中的某一个函数一定是一个双射函数(这取决于链的“起点”属于A还是B)。把它们全部合起来,最终仍然是一个双射函数。
参考资料:
http://www.cut-the-knot.org/WhatIs/Infinity/Bernstein.shtml
http://en.wikipedia.org/wiki/Cantor–Bernstein–Schroeder_theorem
呵呵,沙发
有什么实际用途?
我觉得下面这个证明比较有意思。
考试翘了吗?
这个证明……
>>明天考英语,单词还没背。先冒死更新一个^_^
明显是套取我的留言 ^_^
考试加油~
莫挂了哈
应该会挂吧……不过我相信你的RP……选择题多对几个
第一种证明似乎不够严密,[B∪Y] – [Y∪f(X)] = B-f(X)并不那么显然。因为一般来说[A∪B] – [B∪C] = A-B-C。
没有问题,因为B和Y的交是空的
刚学实数理论,来瞻仰一下.
路过,不知道这个是不是Bernstein定理关于基数三歧性的描述……
证明存在性的话可以用 基数相等的定义 + 两个单设说明|A|<=|B| , |B|B的双射。
用zorn引理能证明么
这个引理真的好啊,厉害