趣题：斜边上的动点

      

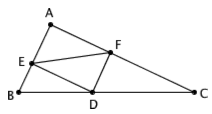
    这是一个非常经典的问题。如图，三角形 ABC 是一个直角三角形， ∠A = 90° 。 D 是斜边 BC 上的一个动点。过点 D 作 AB 和 AC 的垂线，垂足分别为 E 和 F 。问题：当 D 点运动到什么位置的时候，线段 EF 最短？


 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

      

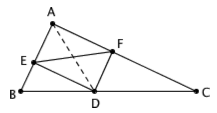
    答案出人意料地简单：当 AD 垂直于 BC 时，线段 EF 最短。这是因为，四边形 AEDF 永远是一个矩形，它的两条对角线永远一样长。因此，为了让 EF 最短，我们只需要让 AD 最短即可。什么时候 AD 最短呢？显然，当 AD 垂直于 BC 时， AD 达到最短。

 
 
      

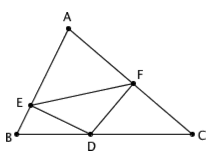
    下面是一个稍微有些挑战性的问题：如果去掉 ∠A = 90° 这个条件，其他条件都不变，那么这一次， D 点应该运动到什么地方，才能让 EF 最短呢？

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

      

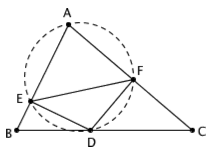
    答案仍然是，当 AD 垂直于 BC 时 EF 最短，不过原因不太一样。注意到，由于 ∠AED = ∠AFD = 90° ，因此 A 、 E 、 D 、 F 四点共圆。在这个圆中， EF 所对的圆周角 ∠A 始终不变。因此，为了让线段 EF 达到最短，我们需要让整个圆越小越好，换句话说这个圆的直径越短越好（这也可以由正弦定理 EF / sinA = 2R 迅速看出）。但是， AD 就是这个圆的一条直径啊！因此，我们需要让 AD 越短越好。什么时候 AD 最短呢？显然，当 AD 垂直于 BC 时， AD 达到最短。

    后面这个问题来自 1987 年 IMO 候选题。

参考资料：Ross Honsberger, From Erdos to Kiev: Problems of Olympiad Caliber, pp. 43-45

16 条评论

发表评论




Enter Captcha Here :