小学奥赛的经典题目：两个人轮流在黑板上写一个不大于10的正整数。规定不准把已经写过的数的约数再写出来。谁最后没写的了谁就输了。问是先写的人必胜还是后写的人必胜，必胜策略是什么。
    答案很巧妙。先写者有必胜策略。他可以先写下数字6，现在就只剩下4、5、7、8、9、10可以写了。把剩下的6个数分成三对，分别是(4,5)、(7,9)、(8,10)，每一对里的两个数都不成倍数关系，且它们各自的倍数（如果出现过）必然是同时出现。因此不管你写什么数，我就写它所在的数对里的另一个数，这样可以保证我总有写的。
    今天偶然看到一个加强版，不知大家见过没有：规则不变，可以写的数扩展到所有不大于n的正整数。对于哪些n先写者必胜？证明你的结论。

    你会有一种被骗的感觉-_-b
    其实，不管n是多少，先写者总有必胜策略。考虑一个新的规则“不准写数字1”。如果加上这个新规则后先写者有必胜策略，那么这个策略对于原游戏同样适用（因为1是所有数的约数，本来就不能写）；如果在新规则下后写者必胜，则原游戏中的先写者写下数字1，然后他就变成了新规则下的后写者。于是不管怎么样，先写者总是有必胜策略。
    To 3楼：忘了提一句，只要是双方共用状态（合法的决策完全相同）的对弈游戏，其中一方肯定有必胜策略。棋局的任一状态只有两种，面对这个棋局的人要么必胜要么必败。考虑这样的一个递推关系：如果一个状态是必胜态，那至少有一种走法能走成一个必败态留给对方；如果一个状态是必败态，那它怎么走都只能走到必胜态。运用这样的关系，我们可以自底向上推出初始状态是必胜还是必败。

    
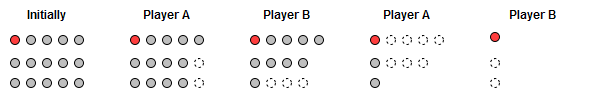
    Update: 感谢网友FreePeter的精彩评论。这种分析方法有一种很形象的名字叫做Strategy-stealing，它的另一个经典例子是Chomp游戏。游戏在一块矩形的巧克力上进行，巧克力被分为MxN块。两人轮流选择其中一个格子，然后吃掉这一格及它右边、下边和右下角的所有格子。最左上角的那一块巧克力有毒，谁吃到谁就输了。上图是一个可能的对战过程。我们可以用类似的方法证明先手必胜。假设后手有必胜策略，那么先手把最右下角的那一块取走。注意到接下来对方不管走哪一步，最右下角的那一块本来也会被取走，因此整个棋局并无变化，只是现在的先手扮演了后手的角色，可以用后手的那个必胜策略来应对棋局，这样便巧妙地“偷”走了后手的必胜策略。
    上面所举的例子都是双方共用状态的游戏（ICG游戏），因此至少有一方存在必胜策略。对于其它一些非ICG游戏，我们也可以用类似的方法证明后手不可能有必胜策略（但在这里并不能说明先手一定必胜）。比如对于井字棋游戏，假设后手有必胜策略，那先手就随便走一步，以后就装成是后手来应对。如果在哪一步需要先手在已经下过子的地方落子，他就再随便走一步就是了。这种证明方法成立的前提就是，多走一步肯定不是坏事。事实上，对于所有这种“多走一步肯定不是坏事”的且决策对称的游戏，我们都可以证明后手是没有必胜策略的。