幸福结局问题，以及一个幸福的结局

    今天是我第一次听说这个故事。

    1933 年，匈牙利数学家 George Szekeres 还只有 22 岁。那时，他常常和朋友们在匈牙利的首都布达佩斯讨论数学。这群人里面还有同样生于匈牙利的数学怪才——Paul Erdős 大神。不过当时，Erdős 只有 20 岁。

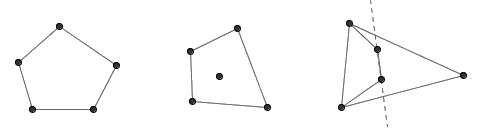
    在一次数学聚会上，一位叫做 Esther Klein 的美女同学提出了这么一个结论：在平面上随便画五个点（其中任意三点不共线），那么一定有四个点，它们构成一个凸四边形。Szekeres 和 Erdős 等人想了好一会儿，没想到该怎么证明。于是，美女同学得意地宣布了她的证明：这五个点的凸包（覆盖整个点集的最小凸多边形）只可能是五边形、四边形和三角形。前两种情况都已经不用再讨论了，而对于第三种情况，把三角形内的两个点连成一条直线，则三角形的三个顶点中一定有两个顶点在这条直线的同一侧，这四个点便构成了一个凸四边形。

    


    众人大呼精彩。之后，Erdős 和 Szekeres 仍然对这个问题念念不忘，于是尝试对其进行推广。最终，他们于 1935 年发表论文，成功地证明了一个更强的结论：对于任意一个正整数 n ≥ 3，总存在一个正整数 m，使得只要平面上的点有 m 个（并且任意三点不共线），那么一定能从中找到一个凸 n 边形。 Erdős 把这个问题命名为了“幸福结局问题”（Happy Ending problem），因为这个问题让 George Szekeres 和美女同学 Esther Klein 走到了一起，两人在 1936 年结了婚。

    对于一个给定的 n ，不妨把最少需要的点数记作 f(n)。求出 f(n) 的准确值是一个不小的挑战。由于平面上任意不共线三点都能确定一个三角形，因此 f(3) = 3 。Esther Klein 的结论则可以简单地表示为 f(4) = 5 。
    当 n = 5 时，八个点是不够的。下图就是八个不含凸五边形的点。

    

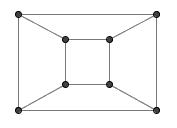
    利用一些稍显复杂的方法可以证明，任意九个点都包含一个凸五边形，因此 f(5) 等于 9 。

    2006 年，利用计算机的帮助，人们终于证明了 f(6) = 17 。对于更大的 n ， f(n) 的值分别是多少？ f(n) 有没有一个准确的表达式呢？这是数学中悬而未解的难题之一。

    不管怎样，最后的结局真的很幸福。结婚后的近 70 年里，他们先后到过上海和阿德莱德，最终在悉尼定居，期间从未分开过。 2005 年 8 月 28 日， George 和 Esther 相继离开人世，相差不到一个小时。

42 条评论

发表评论




Enter Captcha Here :