我们平时习惯说“微积分”。有趣的是，积分的出现远远早于微分。积分思想的早期萌芽甚至可以追溯到古希腊时代，Democritus曾运用这种思想解决了很多复杂的问题。他的“数学原子论”观点强调几何体是由一个一个面重叠而成，而面则是由线组成。他把圆锥看作一个个不可再分的薄片，从而成功地得到了圆锥体体积公式：圆锥的体积等于等底等高的圆柱体体积的1/3。事实上，仅仅凭借经验加实验，这个公式也很容易被发现，因此我们这里不再仔细追究公式的推导过程。但古希腊人对球体积的研究却迟迟没有进展。此时，一代神牛Archimedes出现了。Archimedes用了一种出人意料的神奇方法找到了球的体积公式，整个推导过程令人称叹不已，拍案叫绝。
    我们从圆的方程开始说起。首先观察方程(x-a)^2 + y^2 = a^2，这是一个中心在(a,0)，半径为a的圆，它在y轴右边与y轴相切。整理一下这个式子，我们有x^2 + y^2 = 2ax。在这个式子中，x可以从0取到2a，每一个x的值就对应着一个y值，它表示圆上对应位置的半弦长。注意到这个式子的特殊性：如果等式两边同时乘以π，牛B东西就来了：πx^2 + πy^2 = 2aπx，左边出现了两个与圆面积相关的项。这使我们有了一种让等式两边再乘以一个2a的冲动，因为这样的话等式右边也出现了一个与2a相关的圆面积：2a(πx^2 + πy^2) = x π(2a)^2。现在的问题是，等式左边多出来的一个2a和等式右边的那个x该咋办？不用担心，我们不是有杠杆原理这种牛B东西么，这两个东西可以当力臂长啊。于是，一个现在看上去并不算太突兀的力学模型出现了：

      
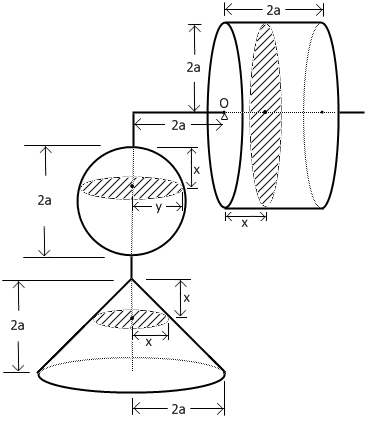
    找一根不计重量的金属杆，水平放置这根金属杆并以O为支点。金属杆右边串一个半径和高都是2a的圆柱体，圆柱体的左端点与支点O重合。把一个半径为a的球和一个底面半径和高都是2a的圆锥用绳子串起来，悬挂在左边距支点2a处。再次回到我们刚才的等式2a(πx^2 + πy^2) = x π(2a)^2。发现了吗，每取一个x，式子中的三个圆面积公式正好对应着这三个几何体相应位置上的横截面积。右边的圆柱横截面积始终为π(2a)^2，它离原点的距离为x；左边那个圆锥的横截面积为πx^2，它与圆锥顶端的距离为x；圆锥上方的那个球里同样存在一个对应的截面，这个截面离球的顶端距离也是x，而它的面积则正好是πy^2（回忆之前提到的半弦长）。乘上它们各自的力臂，我们就得到了上面的式子，而这个式子左右两边是相等的。于是我们知道了，对于任何一个x，三个立体图形对应位置上的“切片”都能够使杠杆平衡。我们有理由相信，如果每一个切片都可以使杠杆平衡的话，取遍所有的切片后，整个系统也应该是平衡的。尽管这存在一个严密性的问题，但毫无疑问这种假设是非常合理的，并且这种想法很大程度上促成了后来微积分的产生。无论如何，Archimedes利用这种方法得到了正确的答案：假设球的体积是V，则由杠杆原理得2a*(V + π(2a)^2*2a/3) = a π(2a)^2*2a （右边那个圆柱体的重心在图形的正中间，它到支点的距离为a，这即是臂长）。解得，V=(4/3)πa^3。

Matrix67原创
做人要厚道
转贴请注明出处