最近在看Pólya的《数学与猜想》,读到了一些很有意思的东西,在这里和大家分享。
我们首先来看一道很火星的题目:A、B两点在已知直线的同侧,请在直线上找出一点C使得∠ACB最大。可能大家都知道这个该怎么做,但这个解法到底是怎么想到的呢?《数学与猜想》提到了这样一种看法:
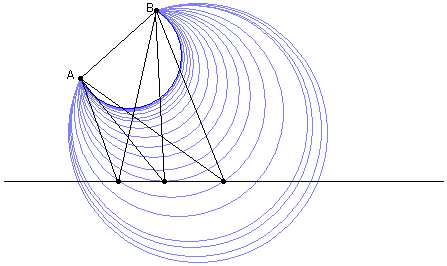
首先,我们需要确定,这条直线上的确存在一点,使得这个角度达到最大。我们很容易观察到,这个动点往左移(可以一直移动到BA的延长线与直线的交点),这个角度会慢慢变小;同时,动点不断往右移时角度也会慢慢变小(在无穷远处角度为0)。可以想到,角度大小的变化可以用一个凸函数来表示,这段函数上一定存在一个最大点。现在任意在直线上取一点C,你怎么才能说明∠ACB是最大或者不是最大?一个比较直观的方法是,如果你取的C点不能使角度达到最大,那么这条直线上一定存在另一个点C',使得∠ACB=∠AC'B。分析到这一步,问题终于有了眉目,因为有一个大家都很熟悉的东西恰好与角度相等有关——同一段弧所对的圆周角总是相等。过点AB作一系列的圆,那么同一个圆周上的所有点对AB的张角都是一样大的。我们看到,这些蓝色的线条与直线的交点都是成对出现,换句话说ABC三点确定的圆与直线的另一个交点就是那个C'。但有那么一个点非常例外:在这无穷多个圆中,有一个圆恰好与直线相切。这个切点只出现了一次,它就是角度大小的极大值。
真正的数学家会从这个简单的题目里看到一些更深的思想。我们可以把这个图任意的扭曲,从而得到这样一个有趣的结论。假设我和MM在野外探险,地形是任意给定的,我们的行动路线也是任意给定的。现在我有一张非常精确的等高线地图,我把我们的路线画在地图上,那么整个旅途中所到达的最高点和最低点在地图上的什么位置?仔细思考等高线的定义,我们立即想到:路径穿过等高线的地方肯定不会是最高点或最低点,因为穿过一条等高线即表明你正在爬上爬下。因此,达到最高点或最低点的地方只能是等高线与我的路线相切的地方。这给我们一个启发:我们可以用这种模式来解决很多极大极小问题。我们把所有可能的结果的分布情况用等高线表示,而实际允许的初始条件则被限制在了一条路径上,那么最优解必然是这条路径与某条等高线的切点。用等高线模式来解释刚才的问题将变得非常简单:图中的蓝色线条就是角度大小的“等高线”,在直线上取得极值的时候,等高线恰与直线相切,其它情况下角度大小都在“变化进行时”。
我们再来看三个有趣的例子。在第一个例子中我们将解释为什么点到直线的距离以垂线段最短,第二个例子则将探究为什么所有的圆内接n边形以正n边形最大。在第三个例子里我们将提到一个与椭圆有关的神奇性质。
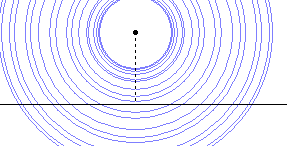
上面这个图就是到定点距离大小的等高线图。我们可以立即看到,等高线就是一个个的同心圆。与已知直线相切的那个同心圆确定了直线到给定点距离最短的位置,而圆的半径与对应位置上的切线垂直,这就说明了点到直线的距离以垂线段最短。
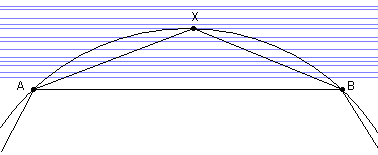
下面我们考虑圆内接多边形的某个顶点X。这个顶点两旁的点分别是A和B。那么整个多边形被分成了两部分:三角形AXB,和剩下的那一大块多边形。如果我们只移动点X,这只会影响三角形AXB的面积,对剩下的部分没有影响。X在不同位置所得到的三角形面积不同,在图中我们用蓝色的等高线来表示这个面积值的分布情况。由于等底等高的三角形面积相同,因此我们的等高线是一系列互相平行的直线。点X只能在一段圆弧上取,当△AXB达到最大时X必然落在圆弧与某条直线相切的地方,显然此时AX=BX。换句话说,只要圆内接多边形里有长度不等的邻边,那么这个多边形的面积一定可以变得更大。再换句话说,只有所有边都相等了,面积才可能达到最大。这就说明了,所有的圆内接n边形以正n边形最大。
我相信你已经对这个方法非常熟悉了,因此最后这个例子我就不画图了。在第三个例子中,我们将考虑一个和光学有关的性质。给定一条直线和直线同侧的两点A、B,那么直线上一定有一点C使得AC+BC达到最小。这个点C是一个以A、B为焦点的椭圆形等高线与直线的切点。固定点A和点B,适当调整直线的位置,结论始终成立。还记得Fermat原理吗,光从一点到另一点总是沿着光程最短的路径来传播。仅考虑反射定律,这个结论很显然。也就是说,A->C->B这样的光线传播路径完全遵循光的反射规律。嘿!我证明了这样一个富有传奇色彩的结论:椭圆形从一个焦点发射出来的光线总会反射到另一个焦点。
做人要厚道
转贴请注明出处
第一次sofa
非常喜欢这些文章。
[smile]
很厉害,你的文章很好.
佩服~~
小兄弟毕业了没?
圆内接多边形的那个证明不完全。就你文中所达到的逻辑地步而言,只能说明非正多边形的面积不会是最大,但因为你没有论证最大面积多边形的存在,因此不能马上说正多边形的面积一定最大。
回复:面积最大的多边形显然存在,因为多边形的面积有一个上限(圆面积);考虑命题“非正多边形的面积不是最大“的逆否命题“一个多边形面积最大,则它是正多边形”,这两个命题同真同假,证明了前者即证明了后者
我与Kuphrer重合……
关于你那个野外探险中所运用的方法也是有问题的。假如你与MM恰好行至某等高线上,此时MM终于向你表白她根本不爱你,你伤心欲绝,也不管自己所走路线是否连续可微什么的掉头就走,这就最终造成你的方法的有效性与你的色情……我是说爱情同时付诸流水。我说得对不对?[smile]
数学与猜想中Polya所以要预先说明最大点确实存在,其原因就是很有可能它并不存在。
回复:您是数学教师吗?我刚在一个教学论坛上看到您了
不对。有上界只能说明面积有上确界,但能不能达到这个上确界则是需要商榷的。
我不是数学教师,只是一个跟你同级的学生罢了~
"考虑命题“非正多边形的面积不是最大“的逆否命题“一个多边形面积最大,则它是正多边形""
其实并不对等,你暗中做了一个假定,即“需要有一个最大面积的多边形”。但这种存在性并不那么显然。
呼~连Steiner在证明周长相等的所有曲线中圆围出的面积最大的证明中都隐隐地有类似的错误。他全部的证明只是说明这个问题:周长相等的曲线中,如果存在一个围出的面积是最大的图形,那么它一定是个圆。但是他自始至终没有证明这样的图形应当是存在的。
其实主要是出于对你的文章的喜爱(呃……也许我应该老实点说崇拜?[wink])才来留言的……很多文章都非常有趣(除了集合{MM})……希望能交个朋友~呵呵
椭圆形从一个焦点发射出来的光线总会反射到另一个焦点.其实可以用平面几何的方法证明
呃……“非正多边形的面积不是最大“的逆否命题啊……
这个感觉是证明的关键……
最大是否存在……这个问题怎么说明呢……
高中竞赛时候觉得这种细节好像都忽略了……
大家说的这个疑问其实很容易证明的。
首先声明,大家讨论的这个问题说的是圆内接n边形面积有无上界。
那么,说明如下:
圆内接n边形,分为两种,n边全相等,n边不全相等,没有别的。
那么显然,面积的最大值,即我们所谓的上界,必然是所有圆内接n边形中的一个或几个,因为面积的大小显然可以比较。
接下来就是Matrix67的思路了:
我们对于每一个n边不全相等的圆内接n边形,都可以通过调整来得到另一个面积更大的圆内接n边形,其n边可能全相等或不全相等。
因此,面积的最大值,显然不是n边不全相等的圆内接n边形。
但圆内接n边形,刚才说了,面积是有最大值的。
而圆内接n边形,除了n边不全相等的,只有n边全相等的那一个了。
所以我们得到结论,n边全相等的是圆内接n边形中面积最大的。
我的一点想法,如果有什么不对的,望各位大牛多多指教。
这种证明需要再严格化一点,就是证明最大值是存在的。这对这种有界图形其实也是显然的,用连续函数在紧集上最值的存在性即可
这并不是另类策略,而是极值问题的通法。这种思路再往后发展就是求条件极值的拉格朗日乘子法,理论上对足够光滑的情形都可以求