2007-07-27 19:54| 
14 Comments | 本文内容遵从
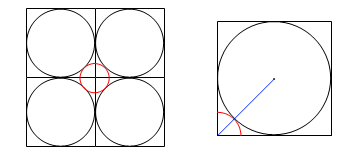
我们把一个边长为2的正方形划分成4个小正方形，每个小正方形里作一个内切圆，然后在原来的大正方形中间作一个同时外切于这4个圆的小圆（红色标注）。我们把这个小圆叫做“中心圆”。你怎么来求这个中心圆的半径？
仔细观察其中一个小正方形，思路就出来了：红色的中心圆变成了一个90度扇形，它的中心位于单位正方形的一角，并且外切于直径为1的圆。可以看到扇形半径加上圆的半径等于单位正方形对角线的一半，这样我们就得出，中心圆的半径等于(sqrt(2)-1)/2。
对于一个立方体同样如此。我们把立方体切成8个小立方体，得到的8个球体中间夹住的那个中心球半径就应该为(sqrt(3)-1)/2。你会发现一个惊人的事实，在超立方体中，位于16个四维球体间的中心球半径为(sqrt(4)-1)/2 = 1/2，它竟然与那16个小球一样大。真正可怕的事情发生在九维立方体中，此时的九维中心球半径为(sqrt(9)-1)/2 = 1，竟然内切于最初的九维立方体！而到了十维空间后，中心球的直径将超过十维立方体的边长，这个中心球将突破立方体的边界！被围在里面的中心球居然比原来的N维立方体还大，这显然违反了大多数人的直觉；如果你能想象出这个画面来，你就牛B了。科幻小说中把对十维空间的感知能力作为文明发达程度的标准，除了一些相关的宇宙模型外，这可能也是其中一个原因吧。
14 条回复
您也随便说几句吧：
沙发
错别字
作为生活在三维空间里的生物的我们, 基本上是很难用直觉想像高维空间的, 因为直觉的建立是一个长期的过程, 我们在三维空间里生活了很久才有了对三维空间的直觉的, 有实验显示, 婴儿对面前的沟深浅就没有什么认识..
回复：错别字已改……为什么中文没有什么有效的拼写检查呢
三维低等生物路过。
实在是想像不出高于三维的情况
无语中～
人类实在是太低等了～
回复：四维立方体很容易想象嘛
well, it's....difficult to imagine[flower]
我觉得奇怪的是,"我们竟然能够在2纬平面里化出三为物体来",如果适当的话,二为平面也能够表现四纬物体.
依次类推,我的问题:1.三纬中如何"表示"四纬物体?
2.低纬到底能够表现多高的纬度,是否有个限度?例如:二为平面能够画出5,6,7,8...纬?还是说最多只能够表现到某个纬度.
呵呵,一些迷惑而已,无聊遐想,如果火星的话,甘愿被b4
回复：按照我的理解，平面上可以画出任意高维的图形；网上有这些图片，可以google一下
实在难以想像
不过想到的更厉害
矩阵可以表达任何多维的模型
你的眼睛能够直接“捕捉”一个二维平面，对一个三维物体，如果能捕捉到足够多的它在二维平面上的投影，使你能够通过这些投影判断它的物理性质，那么你就“感受”到了一个三维物体。同样适用于三维表述四维，要得到足够多的四维物体在三维空间的投影。
没有限度，关键在于能否判断它的物理性质。
真折磨想象力
中心球的直径将超过十维立方体的边长，这个中心球将突破立方体的边界！被围在里面的中心球居然比原来的N维立方体还大
第一句话对, 后面两句错
回复：能说一下为什么吗
惊叹于你对数学的痴迷和数学推理，不过我不大赞同你推理的一个结论“被围在里面的中心球居然比原来的N维立方体还大”，这个可能直觉化了。
下面的推理，不一定对，仅作参考
按照你的推理，n维空间，中心球的半径是(sqrt(n)-1)/2，初始大立方体边长为2
那么大立方体的“容积”是2^n
中心球的呢，a*pi*((sqrt(n)-1)/2)^n，a是系数，2维时a=1，三维时a=4/3，……
那么中心球与大立方体体积比=a*pi*(sqrt(n)-1)^n/2^2n，我们只要看看这个比值随着n怎么变化就知道中心球是否会“撑爆”大立方体了
我不确定系数a和维数n的函数关系，按照2维和3维猜测或许是2^(n-1)/n，如果是对的，可以判断比值函数是否递减
简单不严谨的，看看2维和3维情况下这个比值变化或许能猜测这个函数递减，那么又一个奇怪的高维现象发生了，中心球直径逐渐超过立方体边长，但却撑不爆那个立方体
当然了，中心球的“容积”也是越来越大的，只是增长速度赶不上立方体
回复：分母的底数为常数，但球的半径不断增加，最终体积显然会超过立方体
这个“比值”与你想像的很不一样，有兴趣你可以查一下多维球体积公式的相关资料
感觉那个半径计算公式应该是不正确的，感觉而已哈哈~ 数学上尽管有违反直觉的地方，但是感觉这个地方不是的，里面的N维小球球应该还是包含于N维方体的。不知道楼主的推论是否有确切出处。。。
ms有一部科普电影《dimension》讲四维空间讲的比较形象。。